• 为保证分支预测有效，应让具有相同逻条件和逻辑的运算处于同一程序块中，如：

    • 1、调整循环层数和规模，使底层紧凑 ``` public class BranchPrediction { public static void main(String args[]) {
      long start = System.currentTimeMillis(); for (int i = 0; i < 100; i++) {

      1. for (int j = 0; j <1000; j ++) {
      2.     for (int k = 0; k < 10000; k++) {
      3.     }
      4. }

      } long end = System.currentTimeMillis(); System.out.println(“Time spent is “ + (end - start));

      start = System.currentTimeMillis(); for (int i = 0; i < 10000; i++) {

      1. for (int j = 0; j <1000; j ++) {
      2.     for (int k = 0; k < 100; k++) {
      3.     }
      4. }

      } end = System.currentTimeMillis(); System.out.println(“Time spent is “ + (end - start) + “ms”); } }

//output Time spent in first loop is 5ms Time spent in second loop is 15ms

  2.       - 这个差异就是因为分支预测。循环本质也是利用cmp和jle这样的先比较后挑战的指令来实现的，每一次循环都有一个 cmp 和 jle 指令。每一个 jle 就意味着，要比较条件码寄存器的状态，决定是顺序执行代码，还是要跳转到另外一个地址。也就是说，在每一次循环的时候，都会有一次“分支”。
  3.       - 2、调整循环逻辑顺序，使之有一定的有序性

include

include

include

int main() { // 随机产生整数，用分区函数填充，以避免出现分桶不均 const unsigned arraySize = 32768; int data[arraySize];

  1. for (unsigned c = 0; c < arraySize; ++c)
  2.     data[c] = std::rand() % 256;
  4. // !!! 排序后下面的Loop运行将更快
  5. std::sort(data, data + arraySize);
  7. // 测试部分
  8. clock_t start = clock();
  9. long long sum = 0;
  11. for (unsigned i = 0; i < 100000; ++i)
  12. {
  13.     // 主要计算部分，选一半元素参与计算
  14.     for (unsigned c = 0; c < arraySize; ++c)
  15.     {
  16.         if (data[c] >= 128)
  17.             sum += data[c];
  18.     }
  19. }
  21. double elapsedTime = static_cast<double>(clock() - start) / CLOCKS_PER_SEC;
  23. std::cout << elapsedTime << std::endl;
  24. std::cout << "sum = " << sum << std::endl;

}

//output

1. 取消std::sort(data, data + arraySize);的注释，即先排序后计算

10.218 sum = 312426300000

2. 注释掉std::sort(data, data + arraySize);即不排序，直接计算

29.6809 sum = 312426300000

  2.       - 除去增加clock()代码的方式，也可用perf直接对原项目分析：，找到增加耗时的原因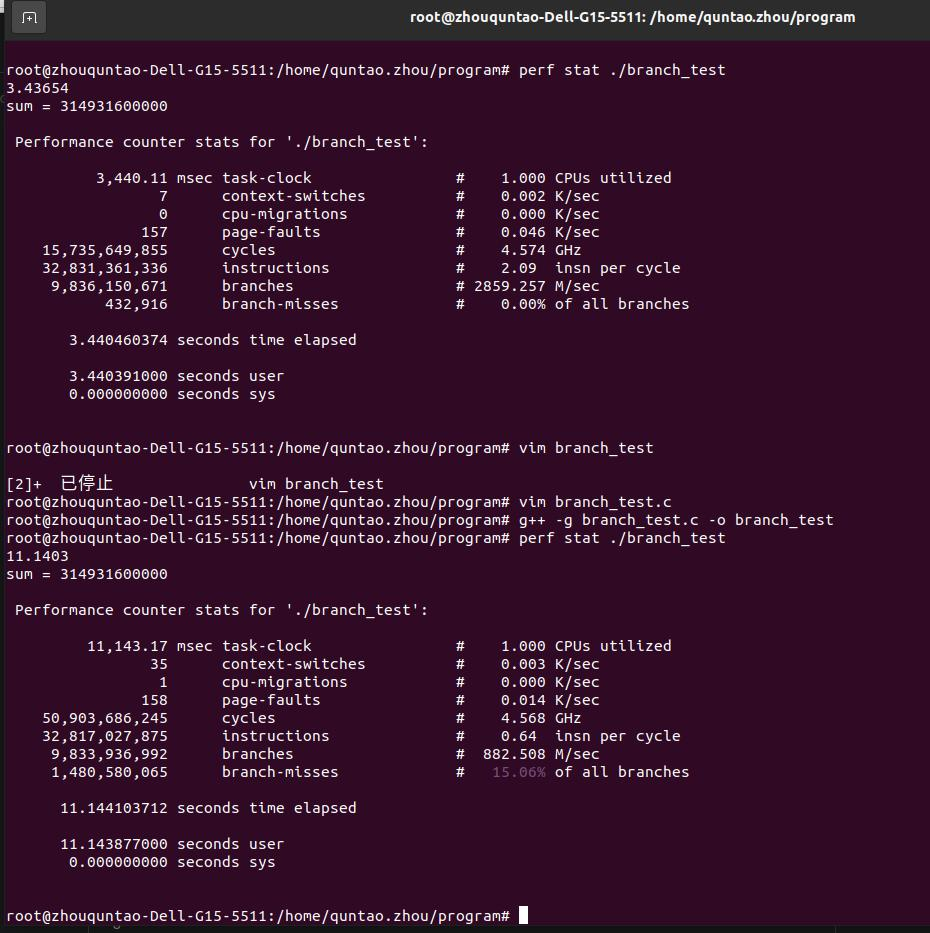
  4. ![图片.png](https://cdn.nlark.com/yuque/0/2022/png/2861023/1649922464619-89a4836e-e042-486d-896f-06589d1e282d.png#clientId=u2a17b4b6-2e02-4&crop=0&crop=0&crop=1&crop=1&from=paste&height=933&id=fa9tK&margin=%5Bobject%20Object%5D&name=%E5%9B%BE%E7%89%87.png&originHeight=933&originWidth=930&originalType=binary&ratio=1&rotation=0&showTitle=false&size=646535&status=done&style=none&taskId=ub04bcc9b-4c67-46f8-b45e-81f414b4396&title=&width=930)    
  6.       - 很明显的看到产生了及其巨大的branch-misses增加，这就是耗时的主要元凶
  9.       - 简单地分析一下：<br />有序数组的分支预测流程：

T = 分支命中 N = 分支没有命中

data[] = 0, 1, 2, 3, 4, … 126, 127, 128, 129, 130, … 250, 251, 252, … branch = N N N N N … N N T T T … T T T …

  1.    = NNNNNNNNNNNN ... NNNNNNNTTTTTTTTT ... TTTTTTTTTT  (非常容易预测)
  1. 无序数组的分支预测流程：

data[] = 226, 185, 125, 158, 198, 144, 217, 79, 202, 118, 14, 150, 177, 182, 133, … branch = T, T, N, T, T, T, T, N, T, N, N, T, T, T, N …

  1.    = TTNTTTTNTNNTTTN ...   (完全随机--无法预测)
  1. 在本例中，由于data数组元素填充的特殊性，决定了分支预测器在未排序数组迭代过程中将有50%的错误命中率，因而执行完整个sum操作将会耗时更多。
  3.       - 优化：利用位运算取消分支跳转，是条件判断情况一致可预测，不会回退

|x| >> 31 = 0 # 非负数右移31为一定为0 ~(|x| >> 31) = -1 # 0取反为-1

-|x| >> 31 = -1 # 负数右移31为一定为0xffff = -1 ~(-|x| >> 31) = 0 # -1取反为0

-1 = 0xffff -1 & x = x # 以-1为mask和任何数求与，值不变

故分支可优化为： int t = (data[c] - 128) >> 31; # statement 1 sum += ~t & data[c]; # statement 2

避免移位操作版： int t=-((data[c]>=128)); # generate the mask sum += ~t & data[c]; # bitwise AND ```

  1.   - 分析：
  2.      1. data[c] < 128, 则statement 1值为: 0xffff = -1, statement 2等号右侧值为: 0 & data[c] == 0;
  3.      1. data[c] >= 128, 则statement 1值为: 0, statement 2等号右侧值为: ~0 & data[c] == -1 & data[c] == 0xffff & data[c] == data[c];

故上述位运算实现的sum逻辑完全等价于if-statement, 更多的位运算hack操作请参见bithacks.
若想避免移位操作，可以使用如下方式：