【差分数组】对区间两端操作代替对区间的操作

• 举例： /LeetCode 995: Minimum Number of K Consecutive Flips@Description:In an array A containing only 0s and 1s, a K-bit flip consists of choosing a (contiguous) subarray of length K and simultaneously changing every 0 in the subarray to 1, and every 1 in the subarray to 0.
  Return the minimum number of K-bit flips required so that there is no 0 in the array. If it is not possible, return -1.
  Note:1 <= A.length <= 300001 <= K <= A.length/
  /思路：差分数组1. 对于若干个K位翻转操作，改变先后顺序并不影响最终结果。因此从头遍历，只翻转 A[i] == 0的子数组2. 翻转操作是唯一的3. 采用差分数组，不翻转数字，统计每个数字需要翻转的次数。一次翻转相当于将子数组中所有数字的翻转次数+14. 遍历到A[i]时，若A[i]+revCnt为偶数，则当前位为0，需要翻转[i, i + K - 1]/class Solution {public: int minKBitFlips(vector& A, int K) { vector diff(A.size() + 1); int res = 0, revCnt = 0; for (int i = 0; i < A.size(); ++i) { revCnt ^= diff[i]; if (A[i] == revCnt) { if (i + K > A.size()) return -1; ++res; revCnt ^= 1; diff[i + K] ^= 1; } } return res; }};
  
• 设reA[i]表示数组第i位的翻转次数，d为reA的差分数组，定义为：
• 
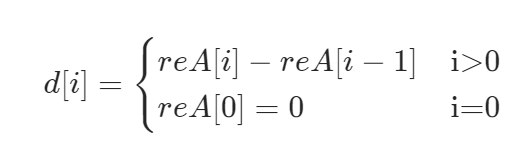
• 从0累加至第n项，得：
• 
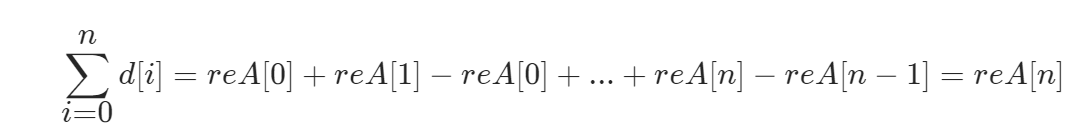
• 即：
• 当数组A的[i, i + K - 1]发生翻转时，
• 
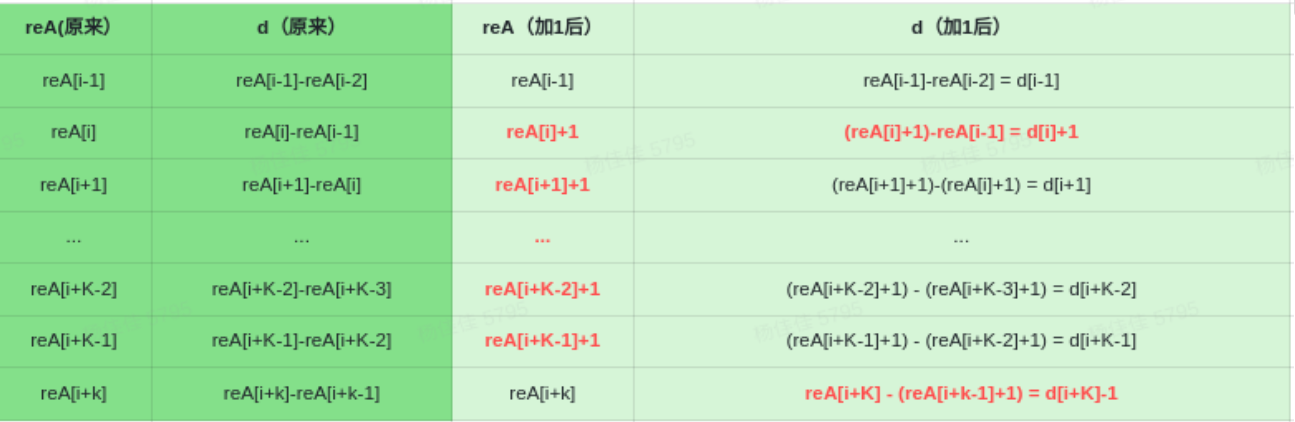
• 若(A[i] + reA[i)] % 2 == 0，则需要翻转；否则不需要