热身:用一个快速的基于矩阵的算法,来计算神经网络的输出
探讨反向传播算法之前,我们先热热身,先介绍一个快速的基于矩阵的方法,用它来计算神经网络的输出。实际上在上一张快结束的时候,我们已经看到这个算法的大概了,现在我们了解一下它的细节。这对于习惯反向传播算法中的各种符号是一个不错的方法。 我们从一个比较难的符号开始,w_{jk}^l他代表了第(l-1)层的第k个的神经元到第l层的第j个神经元之间连接的权重。例如,下图展示的是第二层中第四个神经元到第三层第三个神经元之间连接的权重。
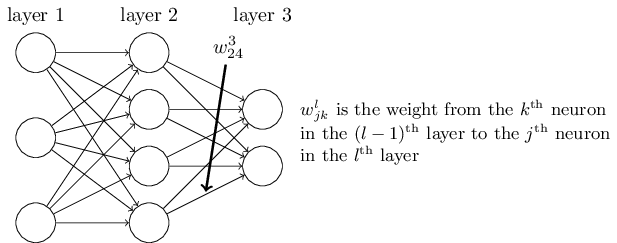
一开始,看起来有些难懂,确实需要花些时间来掌握它。不过,花些功夫你就会发现它其实很简单和直观了。可能你会认为,用j来描述输入神经元用k描述输出神经元会更加直观一些。稍后我会解释为什么会是这样。
在标记网络中的偏移量和激活值时,我们会使用相同的逻辑。b_j^l表示第l层的第j个神经元的偏移量,a_j^l表示第l层第j个神经元的激活值。下图是一个例子:
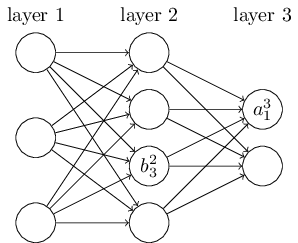
基于这些标记,第l层第j个神经元的激活值a_j^l和第l-1层神经元的激活值有关系,等式如下:
aj^l = \sigma \left ( \sum{k}^{ } w_{jk}^{l} a_k^{l-1} + b_j^l \right ), \qquad \qquad \qquad (23) $$
这里对视对l-1层的所有k个神经元求和。为了使用向量重写这个等式,我们把wl定义为第l层的权重矩阵。权重向量wl的单个实体是连接l层所有神经元的权重。也就是说第j行第k列的权重是w{jk}^l。类似,对于每一层的偏移量b,我们定义向量b_l。你可以已经猜测出来了,偏移量向量的每一个实体为b_j^l,它代表的是第l层的每一个偏移量。最后,我们定义激活值向量a_l,它的每一个元素为a_j^l。
我们要重写等式23的最后一个元素是向量化其中的函数,例如σ。上一章我们简单提到过,这里回顾一下。想法是对向量中每一个元素执行\sigma函数,使用\sigma (v) 来标记。也就是,\sigma (v) 的每一个组成部分\sigma (v)_j = \sigma (v_j)。举个例子,如果函数f(x)=x^2。 向量形式的f函数效果如下:
$$\begin{pmatrix}
\begin{bmatrix}
2 \
3
\end{bmatrix}
\end{pmatrix}
=
\begin{bmatrix} f(2)\ f(3) \end{bmatrix}
=
\begin{bmatrix} 4\ 9 \end{bmatrix}, \qquad\qquad\qquad (24) $$
向量化的f函数会对向量中的每一个元素执行平方计算。
有了这些标记,等式(23)可以被重写为如下等式:
a_l = \sigma (w^la^{l-1} + b_l) \qquad\qquad\qquad (25) 这个等式可以让我们从整体上看到第l层的激活值a_l是如何从第l-1层的激活值a^{l-1}$$中计算得来的:我们把l-1层的激活值乘以对应的权重,然后加上对应的第l层的偏移量。最后在计算σ函数。整体视角经常要比单个神经元视角看起来更简洁和容易。它可以帮助我们避免去理解可恶的角标,同时对算法保持精确的理解。向量化的表达式在实际操作中也非常有用,因为大多数矩阵库都提供了快速的矩阵的乘法加法和向量化。实际上,上一章的代码中,在计算网络行为的时候,我们已经悄悄使用了这个表达式。
使用等式25计算a^l的时候,我们顺便计算了中间值z^l ≡ w^la^{l-1}+b^l。这个等式很有用,还是值得命名一下的:我们称z^l为l层神经元的加权输入。本章中,我们会多次使用这个加权输入。等式25有时会以加权输入的形式书写,a^l = \sigma (z^l) 。 值得提到的一点是z^l的元素模式为:aj^l = \sigma \left ( \sum{k}^{ } w_{jk}^{l} a_k^{l-1} + b_j^l \right ) 。 也就是说z^l的元素z_j^l它是l层第j个神经元激活函数的加权输入.

