交叉熵代价函数

“plugins”: [ “katex” ]

当一个高尔夫球手开始练习打高尔夫球的时候，他们往往会花大量的时间练习一个基础的挥杆动作。 然后，慢慢地，他们才会学习其它的击球动作，打高球，学习拉球和后仰球等等。所有这些都是基于他们基本的挥杆练习。同理，我们花了不少精力去理解反向传播算法，这就是我们的基础挥杆练习，是大多数神经网络工作的基础。这一章，我们将会探讨一系列优化原始反向传播算法的技术，从而改善网络的学习。

我们将介绍到的技术包括：选择一个更好的代价函数—- 交叉熵代价函数；四个正则化方法(L1和L2正则，随机失活以及训练集的人工扩展),这些可以使得我们的网络在现有训练集的基础上能够更好地归纳；一个更好的初始化偏移量的方法;一系列有助于选择好的超级函数的诀窍。除此之外，我们也可以浅显概述一下其它几个技术。这些内容相互之间并没有逻辑上的先后关联性，你大可以跳着读你自己感兴趣的部分。大部分的技术我们也将通过代码来实现，以提升第一章中提到的手写数字分类问题。

当然，在神经网络发展处的新技术中的许许多多技术中，这些仅仅是少数的几个。背后的哲学是，为了理解大量的技术，从深入研究少数几个最重要的技术是一个非常不错的入门方法。掌握了这些重要的技术，不仅仅了解他们本身，也有助于加深你理解当使用神经网络的时候，可能会产生什么的问题。需要的时候，你就可以快速理解而并运用其它技术。

交叉熵代价函数

当我们发现自己错了的时候，大部分人都会觉得不开心。 在我刚开始学习钢琴不久，我就开始在听众面前表演。我非常紧张，刚开始演奏，就把音调搞低了一个音高。我很困惑，知道有人指出来我的错误，我甚至无法继续演奏了。我当时非常尴尬。不过，尽管不那么让人开心，在错误中我们也会学习的非常快。你可以想象，我下一次演奏的时候，一定再也不会把音高弄错了。相反，当我们的错误没有很好清楚地定义的时候，我们的学习会很慢。

理想情况下，我们希望我们的神经网络可以从错误中很快地学习。但现实是这样吗？为了回答这个问题，我们举个简单的例子，只包含了一个神经元和一个输入。

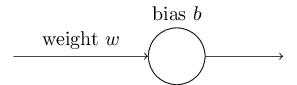
我们将训练这个神经元做些非常简单的事情：输入为1输出结果为0。 当然，这绝对小菜一碟，即使不用学习算法那，我们也可以手工很轻易找到合适的权重和偏移量。但对于使用梯度下降来学习权重和偏移量来说，这个问题很有启发性。我们仔细看一下神经元是怎么学习的。

明确起见，我们将初始权重设为0.6，初始偏移量为0.9。这是在学习开始常用的初始化方法。我并没有选择一些很特别的数值。神经元的初试输出为0.82. 看起来距离我们想要的输出0.0，还有挺多学习要做。你可以试着点击右下角的的运行按钮看看神经网络是如何学习，最终得到的输出为非常接近0.0。请注意，这里并不是一个预设好的动画效果，实际上你的浏览器在实时计算梯度，如何使用梯度来更新权重和偏移量。学习率$\eta = 0.15$，可以看到，它有些慢，不过我们可以跟上整个学习过程，而且可以在几秒钟就可以看完整个学习过程。这里用到的代价函数就是上一章我们提到过的二次代价函数C。我将会不时提醒你所使用代价函数的形式，所以，你不必来回找代价函数的定义。请注意，你可以多次点击”运行”按钮来观看网络的学习过程。

xxxx

如你所见，神经元可以快速地学习权重和偏移量来降低代价函数，最终网络的输出为0.09。虽然距离0.0还有些差距，不过已经相当不错了。不过，假如我们选择的初始权重和偏移量都是2.0.那么，出示输出为0.98，差得有些离谱。我们看下，这种情况下神经元是如何学习，最终得到输出为0的。请再次点击”运行”按钮。

xxxx

这个例子中，我们尽管选择了相同的学习率$\eta = 0.15$，前段部分的学习却十分缓慢。实际上，前150个世代的学习中，权重和偏移量的变化很微弱。然后，学习才突然加速，变得与第一个例子相似，神经元的输出快速趋向于0.0.

和人类的学习曲线相比，这个行为很奇怪。就如本章开头提到的那样，当人类在发现自己错的离谱的时候，往往会学习得非常快。不过，刚才我们看到的却是神经网络在初始阶段虽然错的离谱，学习速度却十分困难—-要比错的没那么远的时候困难得多。其实，不仅仅是这个玩具模式的网络，更多通用的网络也有类似的情况。为什么学习会变慢呢？有办法可以避免这种情况吗？

为了找到这个问题的根源，想象一下，我们的神经元通过改变权重和偏移量进行学习，学习的速度取决于大家函数的导数，$ \frac{\partial C}{\partial w}$ 和$\frac{\partial C}{\partial b}$。所以，所谓的学些比较慢是技术上等同于说这些偏导数很小。挑战是弄清楚为什么会这样。我们来计算一下这个偏导数，我们用到的代价函数如下：

$ C = \frac{(y-a)^2}{2}, \qquad \qquad \qquad (54) $

a是当输入$x=1$时，神经元的输出，y=0是期望的输出。为了更清楚一些，我们使用权重和偏移量来书写。回想一下，$a=\sigma(z)$，$z=wx+b$。运用链式法则可以得到：

$ \frac{\partial C}{\partial w} = (a-y)\sigma’(z)x = a\sigma’(z) \qquad \qquad \qquad (55) $

$ \frac{\partial C}{\partial b} = (a-y)\sigma’(z)x = a\sigma’(z) \qquad \qquad \qquad (56) $

这里我做了个替换$x = 1, y=0$。 为了理解这些表达式的意义，我们看一下等式右侧的$\sigma’(z)$。回忆一下$\sigma$函数：

当神经元的输出接近1的时候，曲线变得非常平坦，所以$\sigma’(z)$的值就很小。等式(55)和等式(56)告诉我们，$\frac{\partial C}{\partial b}$ 和 $\frac{\partial C}{\partial w}$就非常小。这就是学习缓慢的根源了。稍后我们会看到，学习缓慢不仅仅发生在这个玩具神经元网络中，在许多通用神经网络也经常发生。

介绍交叉熵代价函数

那如何解决学习缓慢的问题呢？方法是将二次代价函数换做一个新的代价函数，交叉熵函数。为了理解这个函数，我们先把超级简单的玩具网络模型放在一边。加入我们想训练一个神经元，它由多个变量$x_1,x_2,…，$对应的权重为$w_1,w_2,…$，偏移量为$b$:

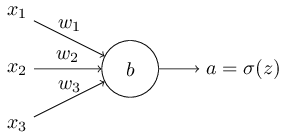
神经元的输出为$a=\sigma(z)$,这里$z=sum_j w_jx_j + b$是对所有的输入进行加权求和。这个神经元的交叉上函数定义如下：

$C = -\frac{1}{n} \sum_x [ylna + (1-y)ln(1-a)], \qquad \qquad \qquad (57)$

这里$n$是训练数据的数量，求和是针对所有的训练集$x$，$y$是对应的期望的输出。

等式(57)可以避免学习缓慢的问题吗？现在还不太明显。甚至，坦率地说，很不太能看出来它是一个代价函数。弄明白它是如何解决学习缓慢之前，我们先看一下它为什么可以用作代价函数。

作为代价函数，它有两个特别的特性。第一，它非负数，C>0。请注意，(a)，等式(57)中，所有的单个元素都是负数，因为两个元素都是对介于0与1之间的数求对数。(b)，在求和运算符之前有一个负号。

第二，对于所有的输入x而言，如何神经元的实际输出接近于期望的输出，那么交叉熵函数的值接近于0.为了弄明白这一点，对于某个输入$x$,$y=0$并且$a \approx 0$。 这个案例中，神经元工作的非常好。因为$y=0$代价函数等式(57)右侧第一项消失了，第二项$-ln(1-a)\approx 0$.运用类似的分析，可以得到$y=1$的时候，$a \approx 1$。由于实际输出接近于期望值，所以它们对代价函数的贡献会比较低。

总结一下，交叉熵函数为正值，给定训练输入x，当神经元计算的结果接近于期望值y时， 交叉熵函数的值趋向0。这都是我们期望代价函数所具备的特性。实际上，二次代价函数也具备这两个特性。这对于交叉熵函数来说是个不错的消息。不仅仅如此，交叉熵函数拥有一个二次代价函数所不具备的特性，避免了学习缓慢的问题。为了证明这一点，我们计算一下交叉熵函数对权重的偏导数。我们把$a=\sigma(z)$代入等式(57),然后应用两次链式法则，就可以得到:

$\frac{\partial C}{\partial w} = -\frac{1}{n}\sum_x(\frac{y}{\sigma(z)}-\frac{1-y}{1-\sigma(z)})\frac{\partial \sigma}{\partial w_j} \qquad \qquad \qquad (58)$

$= -\frac{1}{n}\sum_x(\frac{y}{\sigma(z)}-\frac{(1-y)}{1-\sigma(z)})\sigma’(z)x_j. \qquad \qquad \qquad (59)$

把所有元素放在一个统一的分母上，然后进行简化，可以得到：

$\frac{\partial C}{\partial w} = \frac{1}{n}\sum_x \frac{\sigma’(z)x_j}{\sigma(z)(1-\sigma(z))}(\sigma(z)-y). \qquad \qquad \qquad (60)$

运用sigmoid函数的定义$\sigma(z) = \frac{1}{1+e^{-z}}$,以及一些简单的代数计算，可以得到$\sigma’(z) - \sigma(z)(1-\sigma(z))$。在接下来的联系中，我会要求你去证明这一点，这里，我们先简单接受它。$\sigma’(z)$和$\sigma(z)(1-\sigma(z))$刚好和上述等式抵消，所以等式可以简化为：

$\frac{\partial}{\partial w_j} = \frac{1}{n}\sum_xx_j(\sigma(z)-y). \qquad \qquad \qquad (61)$

这个等式很漂亮。它告诉我们权重学习的率(rate)取决于$\sigma(z)-y$，输出的误差就是其中的一个例子这就意味着，误差越大，神经元的学习越快。这恰好是我们所期望的。而且，他避免了二次代价函数中使得学习缓慢的$\sigma’(z)$,交叉熵函数消除掉了$\sigma’(z)$,再也不用担心因为它是的学习率变小了。这个消除是是交叉熵函数的一个奇迹。其实也不是奇迹，稍后我们将看到，交叉熵函数是我们精心挑选出来的。

同样，我们可以依此来计算偏移量的偏导数。细节这里不再赘述，你可以轻松证明以下等式：

$\frac{\partial C}{\partial b}= \frac{1}{n}\sum_x (\sigma(z)-y) \qquad \qquad \qquad (62)$

再次规避了二次代价函数中让学习变得缓慢的$\sigma]’(z)$项。

练习

• 证明$\sigma’(z) = \sigma(z)(1-\sigma(z)).$

回到我们反复把玩的玩具案例，来看看在使用了交叉熵取代二次函数作为代价函数后，会发生什么。为了能够清楚说明这一点，我们以能够在二次代价函数下良好运作的初始权重0.6和偏移量0.9开始。请点击一下”运行按钮”来看看用交叉熵函数替代二次函数后会是怎样：

xxxx

没有任何问题，和早前一样，神经元学习的非常好。然后，我们在看看二次代价函数表现不太好的情况，我们把偏移量和权重都设置为2.0：

成功了！这次神经元仍然学习的很快，正如我们的预期。如果你仔细看一下，你会发现，初始阶段，在二次代价函数曲线比较平坦的部分，交叉熵代价函数的曲线却陡峭得多。这个交叉熵函数带来的陡峭，使得神经元终于在应该最快学习的时候(例如初始化偏差离谱的时候)，避免了卡壳。

我在这些例子中并未提到学习率。早先，在二次代价函数中，我们使用$\eta = 0.15$。在新的例子中，我们应该使用相同的学习率吗？事实上，因为更换了代价函数，对比学习率似乎也失去了意义。正如拿苹果来对比橘子。对于这两个例子，我只是简单地做了一些实验来找到一个合适的学习率，这样我们可以看清楚到底发生了什么。如果你真的很好奇，我把真想公布出来，刚才的案例中，我使用的学习率是$\eta = 0.005$。

你可能会提出反对，学习率的改变是的对比上述图表变得没有意义了。如果我们随意选择学习率，谁去关心神经元的学习速度呢？这个反对意见脱离了我们讨论的主体。以上图表不是想要标明绝对的学习速度，而且学习速度的变化。具体来说，使用二次代价函数的时候，神经元错的离谱时学习速度反而比之后接近正确输出时候还要慢；但对于交叉熵函数来说，错的越离谱，学习速度越快。这个结论和学习率无关。

我们已经学习了单个神经元的交叉熵函数，多个神经元多层神经网络下的交叉熵函数就不困难了。举个例子，设$y=y1,y2,…$是期望的输出神经元，例如 处于网络最后一层的神经元，$a_1^L,a_2^L,…$是实际的网络计算输出值。那么交叉熵函数如下：

$C = -\frac{1}{n}\sum_x\sum_j[y_jln a_j^L+(1-y_j)ln(1-a_j^L)]. \qquad \qquad \qquad (63)$

这还之前的等式(57)的表达式相同，只不过多了一个$\sum_j$来对所有的输出神经元进行求和。这里就不继续求导了，不过，在很多神经网络中，使用了等式(63)就可以避免学习缓慢的问题。如果感兴趣，你可以自己去求导一下。

顺带提一下，我使用的属于交叉熵函数可能会对一些早期的读者产生困惑，从字面上看，它可能和其它人的叫法有些冲突。一般情况下，会把交叉熵函数定义为两个概率分布，$p_j$和$q_j$，函数为：$\sum_jp_jlnq_j$。这个定义和等式(57)关联性比较强。我们可以把单个sigmoid神经元的输出看作是由神经元激活值$a$及其补数$1-a$构成的概率分布。

不过，如果最后一层的sigmoid神经元有多个的时候，激活值向量$a_j^L$并不会形成概率分布。结果是，因为我们并不是基于概率分布工作的，像$\sum_jp_jlnq_j$的定义甚至失去了意义。相反，你可以把等式(63)当做是对一组单个神经元的交叉熵函数的进行求和，每一个神经元的激活值被解释为一个包含两个元素的概率分布。这种情况下，等式(63)就意味着是对概率分布的交叉熵函数的求和。

那我们应该在什么时候用交叉熵函数代替二次次代价函数呢？是事实上，只要我们选取的simgoid神经元，交叉熵函数几乎总是更好的选择。原因是，我们在初始化权重和偏移量的时候，总是会用随机化方法。所以，有可能我们的初试选择结果对于一些输入来说可能偏的离谱，这样输出神经元要么在0要么1附近饱和，这种情况下，如果使用二次代价函数，学习的速度就会减慢。当然学习不会停止，因为权重还是会不断地从训练输入中学习，不过学习的速度可能会让我们有些失望。

练习

• 交叉熵函数一个棘手的地方是比较难以记住y和a的对应的角色。优势比较难以弄清楚到底是$−[ylna+(1−y)ln(1−a)]$ 还是$−[ylna+(1−a)ln(1−y)]$。 对于第二个表达式，如果y=0或者1的时候，会发生什么呢？这个问题和第一个表达式有关吗？为什么？

• 本节开头我们讨论单个神经元的时候，我们讨论过，对于所有的训练样本来说，当$\sigma(z)\approx y$时，交叉熵函数会是个很小的值。这是基于y要么等于0要么等于1的假定。这对于分类问题往往是适用的，但对于其它问题(例如 回归问题)，y有些时候是介于0和1之间的中间值。此时，对于所有训练样本，当$\sigma(z) = y$时，交叉熵函数仍然是最小化的。这种情况下，交叉熵函数的也是有价值的：

$C = -\frac{1}{n}\sum_j[ylny + (1-y)ln(1-y)] \qquad \qquad \qquad (64)$

$[ylny + (1-y)ln(1-y)]$有时也被叫做二级制熵。

问题

• 多层级多神经元网络

在上一章介绍的编辑中，我们可以看到在输出层，二次代价函数相对于权重的偏导数为： $\frac{\partial C}{\partial w_{jk}^L} = \frac{1}{n}\sum_xa_k^{L-1}(a_j^L - y_j)\sigma’(z_j^L)\qquad \qquad \qquad (65)$

当初始化离谱时，输出神经元项饱和，因此$\sigma’(z_j^L)$这一项造成了学习缓慢。采用交叉熵作为代价函数时,单个训练样本$x$的输出误差为$\delta^L$：

$\delta^L = a^L -y \qquad \qquad \qquad (66)$

代入这个表达式后，在输出层对权重求偏导数的等式为：

$\frac{\partial C}{\partial w_{jk}^L = \frac{1}{n}\sum_xa_k^{L-1}(a_j^L - y_j)}. \qquad \qquad \qquad (67)$

这里$\sigma’(z_j^L)$项消失了，所以交叉熵避免了学习缓慢的问题，这不仅仅对于单个神经元适用，对于多个层级多个神经元构成的网路也适用。稍微变换一下这个分析，你可以看到它对偏移量同样是适用的。如果你还没弄清楚，你需要花些时间自己弄明白它。

• 当输出层是线性神经元的时候，使用二次代价函数。加入有一个多层多神经元的网络，所有最后一次层的神经元都是线性神经元，这就意味着还未应用sigmoid激活函数，输出的结果是$a_j^L = z_j^L$。如果使用二次代价函数，那么对于一个给定的样本输入$x$,输出误差$\delta ^L$：

$\delta ^l = a^L -y. \qquad \qquad \qquad (68)$

和前面的问题类似，使用这个等式来证明输出层对于权重和偏移量的偏导数为：

$\frac{\partial C}{\partial w_{jk}^L} = \frac{1}{n}\sum_x a^{l-1}(a_j^L - y_j) \qquad \qquad \qquad (69)$

$\frac{\partial C}{\partial b_j^L} = \frac{1}{n}\sum_x(a_j^L - y_j). \qquad \qquad \qquad (70) $

可以看到，当输出神经元是线性神经元的时候，二次代价函数并不会造成学习缓慢的问题。这种情况下，二次代价函数作为代价函数是合适的。

使用交叉熵函数分类MNIST手写数字

在梯度下降和反向传播算法的程序中，使用交叉熵函数比较容易。在这张稍后环节我们再这样做，到时候我将基于以前版本的MNIST手写数字输入识别程序(netwrok.py)进行改进。新的程序命名为network2.py。我们将不仅仅用到交叉熵函数，还有用到本章稍后环节讲到的新技术。现在，我们先看一下新的程序在做MNIST数字分类的时候表现的怎么样。和第一章相同，我们将使用30层隐藏神经元，mini-batch包含10个样本。学习率$\eta = 0.5$，将会训练30个世代。network2.py的接口和network.py稍稍不同，不过仍然还是挺容易弄明白发生了什么。你可以在Python shell里面使用诸如help(network2.Network.SGD)的命令得到network2.py的文档。

···

import mnist_loader training_data, validation_data, test_data = \ … mnist_loader.load_data_wrapper() import network2 net = network2.Network([784, 30, 10], cost=network2.CrossEntropyCost) net.large_weight_initializer() net.SGD(training_data, 30, 10, 0.5, evaluation_data=test_data, … monitor_evaluation_accuracy=True)

···

顺便提一下，net.large_weight_initializer()命令来初始化权重和偏移量，方法和第一章描述的一样。在本章稍后环节，我们将改变权重和偏移量的初始化，所以需要运行这样命令。运行上述代码的结果是，我们得到了一个识别准确率为95.49%的神经网络。这和我们在上一章中使用二次代价函数得到的结果95.42%非常接近了。

如果我们看一下当隐藏层为100其它参数不变的时候，使用交叉熵函数会发生什么。这次的准确率达到了96.82%。相对于第一章中使用二次代价函数时我们得到的96.59%的准确率，这个是一个很不错的改进。这可能看起来是一个微不足道的提升，实际上错误从3.41%下降到了3.18%，也就是说相对于改进前的每14次错误，就可以减少一次。这是一个不容忽视的改进。

相对于二次代价函数，交叉熵函数可以提供接近甚至是更好的结果，这令人深受鼓舞。不过，上述结果却不足以证明交叉熵函数一定是一个好的选择。原因是，我并没有花太多精力选择超级参数，无论是学习率、mini-batch的大小等等。为了坐实它的优越性，需要踏踏实实做很多优化这些超级参数的工作。结果仍然是让人欢欣鼓舞的，足够证明我们之前的理论推测。

这也是我们在这章以及本书剩余部分使用的工作模式，我们会不断尝试新的技术，得到提升后的效果，这当然是件让人十分开心的事情。不过，如何理解这些改进就没那么容易了。只有当我们花大量的功夫来优化其它的超级参数后能够看到提升，这才足够有说服力。这就需要投入许多工作，花费巨大的算力才能够达到这一点。我们通常不会这么做。想法，我们会基于类似与上述的非正式测试继续。不过，请记住，这些测试并未经过严禁的验证，时刻保持警惕参数有表现不好的时候。

至此，我们花了一大段来讨论交叉熵函数。看起来对于MNIST的结果并没有太大的提升，那为什么花费这么多的精力呢？本章稍后，我们会介绍其他的技术—- 正则化—-，它将带来明显的提升。为什么要如此关注交叉熵函数呢？一个原因是交叉熵函数是一个广泛运用的代价函数，所以有必要弄个清楚它。另外一个原因是，神经元的饱和化是神经网络的一个重要问题，在稍后环节我们会不是提到它。为了帮助理解神经元饱和化以及如何解决，我花了不小的篇幅来解释它。

交叉熵函数到底意味着什么呢？它是怎么得来的？

我们对交叉熵函数的讨论集中在代数分析和实际的执行。很有效，不过也遗漏了更宽广的概念上的问题，例如：交叉熵函数到底意味着什么？如何直观地理解它？起初，人们为什么是想到交叉熵函数呢？

我们从最后一个问题开始，起初交叉熵函数是如何被发现的？假如，我们已经发现学习缓慢的问题，而且弄明白了其始作俑者是等式(55)(56)中的$\sigma’(z)$，为了解决这个问题，我们会想，是否可以选择一个能够使$\sigma’(z)$消失的代价函数呢？这种情况下，对于单个输入样本$x$，代价函数$C = C_x$就会满足：

$\frac{\partial C}{\frac{\partial w_j}} = x_j(a-y) \qquad \qquad \qquad (71)$

$\frac{\partial C}{\partial b} = (a-y) \qquad \qquad \qquad (72)$

如果我们能够找到一个代价函数来使以上两个等式成立，就可以直觉得认为，初试的错误越大，神经元学习地越快。这样就避免了学习缓慢的问题。事实上，基于这两个等式，凭借着我们的数据嗅觉，就可以导出交叉熵函数。从链式法则我们可以得到：

$\frac{\partial C}{\partial b} = \frac{\partial C}{\partial a}\sigma’(z). \qquad \qquad \qquad (73)$

其中$\sigma’(z) = \sigma(z)(1-\sigma(z)) = a(1-a)$，最后一个等式就变成了：

$\frac{\partial C}{\partial b} = \frac{\partial C}{\partial a}a(1-a). \qquad \qquad \qquad (74)$

与等式(72)对比，我们可以得到

$\frac{\partial C}{\partial a} = \frac{a-y}{a(1-a)}. \qquad \qquad \qquad (75)$

整合为关于a的表达式，可以得到：

$C = -[y ln a + (1-y)ln(1-a)]+contant \qquad \qquad \qquad (76)$

这是一个训练样本$x$对代价函数的影响。为了得到全部的代价函数，我们可以对所有的训练样本求和然后求平均数：

$c = -\frac{1}{n}\sum_x[y lna + (1-y)ln(1-a)]+contant, \qquad \qquad \qquad (77)$

这里常数是单个训练集常数的平均值。所以，我们看到等式(71)和(72)基于总体常数项，独特地定义了交叉熵函数的形式，交叉熵函数并不是凭空奇迹般地出现的。相反，它是我们通过简单和自然的方法发现的。

交叉熵函数的直观解释是什么？我们应该怎么理解它？深度解释这个问题，会超出我期望的讨论范畴。不过，值得一提的是，解释交叉熵函数的一个标准方法是信息理论视角。错略来讲，交叉熵函数是对惊讶程度的度量。具体来讲，我们的神经元试图计算函数$x\rightarrow y=y(x)$。不过它却计算了函数$x\rightarrow a = a(x)$。 加入我们把a认为是神经元对y是1的可能性的估计，1-a是对y是0的可能性的估计。那么，交叉熵函数是用来衡量 往我们学习y的真正的值。xxxx。当输出结果符合我们的预期时，惊讶值是低的，相反，如果输出结果偏离我们的逾期，惊讶值就高。当然，我们并没有明确说惊讶准确来讲意味着什么，这看起来像是空洞的措辞。实际上，有一个精确的信息理论来表述惊讶的含义。不幸的是，我在互联网上没有找到关于这个主题的短小贴切且自包含的定义。不过，如果你想了解深一些，你可以从Wikipedia上的简短描述开始你的探索之旅。而且，在本书第五章中我们会讨论到Cover and Thomas信息理论的Kraft不等式，你的探索会成为这些讨论的素材。xxxx

问题

我们花了相当的篇幅讨论使用二次代价函数时，会发生神经元饱和而使得学习变得缓慢的问题。在等式(61)中，另外一个会影响学习速度的项是$x_j$。由于它，当输入$x_j$接近于0的时候，对应的权重$w_j$的学习也会变慢。解释一下，为什么通过改变代价函数无法消除因$x_j$造成学习缓慢的问题。

softmax(归一化指数函数)

本章的大部分内容我们使用交叉熵函数来解决学习缓慢的问题。这里，我简要介绍一下另外一个解决这个问题的方法，基于对各层的神经元进行归一化指数。本章的剩余部分我们不会使用归一指数化神经元，所以，如果你赶时间，可以跳过这一节。不过，归一化指数函数还是值得了解一下的，一方面是因为它本身很有趣，而且本书第六章中讨论深度学习神经元的时候，我们也会用到归一化指数神经元。

归一化指数函数定义了一种新型的神经网络输出层。它和sigmoid神经元具有相同的加权输入值计算方法，$zj^L = \sum_k w{jk}^La_k^{L-1}+b_j^L$。不过，当计算输出值的时候，我们不使用sigmoid函数。而是对$z_j^L$执行所谓的归一化指数函数。基于这个函数，第j的输出神经元的激活值$a_j^L$的计算公式为：

$a_j^L = \frac{e^{z_j^L}{\sum_k e^{z_k^L}}. \qquad \qquad \qquad (78)$

这里的求和是对所有的输出神经元求和。

如果你对归一化指数函数不熟悉，等式(78)看起来有些费解。而且为什么要使用这个函数也有些难以理解，更不用说，可以用它来解决学习下降的问题了。为了深入理解等式(78)，假如有一个神经网络包含了4个输出神经元，对应有4个加权输入，我们记做$z_1^L,z_2^L,z_3^L,z_4^L$。下图中的每一个滑块都可以通过拖动来调整对应是数值，你可以看到当改变其中一个加权输入值的时候，所有的输出激活值都会随之发生变化。可以先试试改变最下面的滑块来增加$z_4^L$。

xxxx

当你增加$z_4^L$的时候，你会发现对应的输出激活值$a_4^L$会增加，而且其它的输出激活值却在减少。相反，当你减少$z_4^L$，$a_4^L$也会随之减少，但其它的输出激活值则会增加。如果仔细观察，会发现，这两种情况下，其它的激活值会填补$a_4^L$发生的变化。原因是，输出激活值之和恒定为1.可以对(78)进行简单的代数计算来证明这一点：

$\sum_j a_j^L = \frac{\sum_j e^{z_j^L}}{\sum_k e^{z)k^L}} \qquad \qquad \qquad (79)$

结果是，当$a_4^L$增加时，其它的输出激活值必须减少相同的量，以保证它们之和始终保持为1.当然，如果改变其它的任一个激活值时，这个逻辑是同样成立的。

等式(78)也说明了输出激活值都为正值，因为指数函数为正值。结合上一段我们可以看到，归一化指数层的输出是一组正实数且它们之和恒定为1。换言之，可以把归一化指数层的输出看作为概率分布。

将归一化指数输出层当做是概率分布有时候很有用。在很多问题中，把输出激活值$a_j^L$当做是网络对正确输出为$j$的概率的估算会非常方便。例如，在MNIST分类问题中，我们可以把$a_j^L$当做是网络对数字分类结果为$j$的概率的估算。

相反，如果输出层是sigmoid层，那么我们当然不能把激活值当做是概率的分布。无就不证明这一点了，sigmoid神经元输出层激活值无法构成一个概率分布还是挺明显的。所以，对于一个sigmoid输出层来说我们，我们也不会这样去理解输出层激活值。

练习

• 构建一个简单的例子，验证sigmoid输出层网络的输出激活值$a_j^L$之和并不总是为1.

我们开始对归一指数函数及其行为有了写感觉。简单回顾一下：等式(78)中的指数保证了所有的输出激活值都为正数，而且，等式(78)也保证了归一指数函数函数的输出值之和为1。所以，归一化指数函数的具体形态没那么神秘了：这是一个很自然的方法，来保证输出激活值行程一个概率分布。你可以把归一化指数函数当做是一个方法，它把每一个$z_j^L$变形，以便把它们塞进一个概率分布当中。

练习

归一化指数函数的单一性 之前我们提到过，如果$j = k$时，$\frac{\partial a_j^L}{\partial z_K^L}$为正，否则为负。所以，增加$z_j^L$就可以保证增加对应的输出激活值$a_j^L$，同时，会减少其它的输出激活值。稍前我们已经通过滑块直观的了解到这一点，这里请严谨地证明一下。

归一化函数的非本地性

sigmoid函数的一个优点是输出值$a_j^L$是它的加权输入值的单一变量函数$a_j^L = \sigma (z_j^L)$。请解释一下对于归一化函数来说这种关系不成立，输出激活值$a_j^L$取决于所有的加权输入值。

问题

翻转归一化指数函数 加入有一个神经网络的输出层为归一化指数函数，激活值$a_j^L$已知。对应的加权输入值的表达式为：$z_j^L = ln a_j^L + C$，常数C与j无关。

学习缓慢问题： 我们队归一化指数层神经元有不少了解了，不过，它是如何解决学习缓慢的问题的呢？为了弄明白这一点，我们定义一个类对数代价函数。我们把$x$记做网络的训练输入，$y$记做对应的期望的输出。对于这个训练输入的类对数代价函数为：

$C = -ln a_y^L \qquad \qquad \qquad (80)$

这样，假如MNIST图片作为训练集，如果输入为7的一张图片，那么类对数得到代价就为$-ln a_7^L$。