深度优先搜索DFS、广度优先搜索BFS

地上有一个m行和n列的方格。一个机器人从坐标0,0的格子开始移动，每一次只能向左，右，上，下四个方向移动一格，但是不能进入行坐标和列坐标的数位之和大于k的格子。 例如，当k为18时，机器人能够进入方格（35,37），因为3+5+3+7 = 18。但是，它不能进入方格（35,38），因为3+5+3+8 = 19。请问该机器人能够达到多少个格子？

可以用深度优先搜索：每走一步都要判断这一步能不能走，显然最外围一圈不能走，然后根据题意，格子行列各个位加起来不能大于阈值threshold。然后走到下一个格子，走法是一样的，所以可以递归实现。注意：被访问过的格子需要用记录一下。不然会一个格子会被访问多次。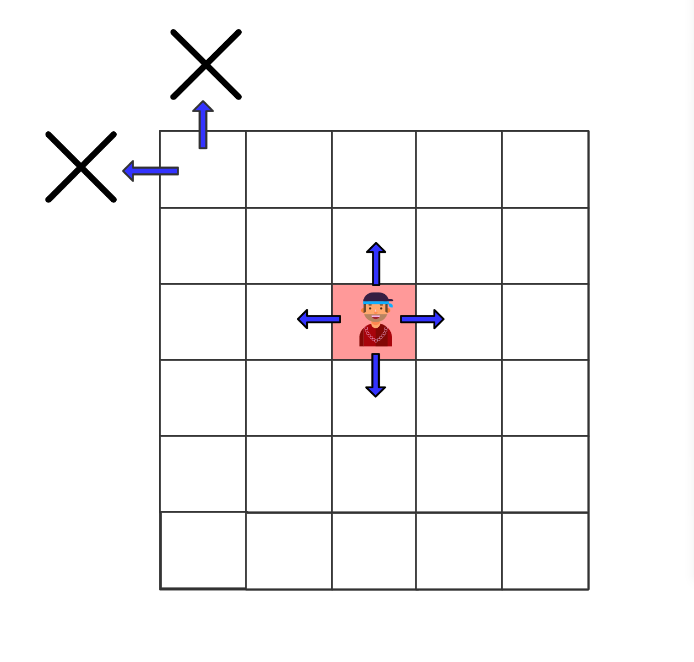

DFS解法

public class Solution {
    public int movingCount(int threshold, int rows, int cols){
        if (rows <= 0 || cols <= 0 || threshold < 0)
            return 0;
        boolean[][] isVisited = new boolean[rows][cols];
        return movingCountIntervals(threshold, rows, cols, 0, 0, isVisited);
    }
    public int movingCountIntervals(int threshold, int rows, int cols, int row, int col, boolean[][] isVisited){
        if (row<0 || row>=rows || col<0 || col>=cols || checkSum(col)+checkSum(row)>threshold || isVisited[row][col]){
            return 0;
        }
        isVisited[row][col] = true;
        //其实当前节点的左节点和上节点已经被访问过了所以下面的movingCountIntervals(threshold, rows, cols, row-1, col, isVisited)和
        //movingCountIntervals(threshold, rows, cols, row, col-1, isVisited)是多余的
        return 1 + movingCountIntervals(threshold, rows, cols, row+1, col, isVisited)
                 + movingCountIntervals(threshold, rows, cols, row-1, col, isVisited)
                 + movingCountIntervals(threshold, rows, cols, row, col+1, isVisited)
                 + movingCountIntervals(threshold, rows, cols, row, col-1, isVisited);
    }
    public int checkSum(int num){
        int sum=0;
        while(num>0){
            sum += num%10;
            num /= 10;
        }
        return sum;
    }
}

BFS解法

import java.util.LinkedList;
import java.util.Queue;
public class BFS {
    public static void main(String[] args) {
        System.out.println(BFS.movingCount(3,10,10));
    }
    public static int checkSum(int num){
        int sum=0;
        while(num>0){
            sum += num%10;
            num /= 10;
        }
        return sum;
    }
    public static int movingCount(int threshold, int rows, int cols){
        if(rows<=0 || cols<=0 || threshold<0)
            return 0;
        int result=0;
        //BFS
        Queue<Integer> queue = new LinkedList<>();
        boolean[][] isVisited = new boolean[rows][cols];
        queue.offer(0);
        while(!queue.isEmpty()){
            int row = queue.peek()/cols;
            int col = queue.peek()%cols;
            if(row<rows && col<cols && checkSum(row)+checkSum(col)<=threshold && !isVisited[row][col]){
                result++;
                isVisited[row][col] = true;
                queue.offer((row+1)*cols+col);
                queue.offer(row*cols+col+1);
            }
            queue.poll();
        }
        return result;
    }
}

DFS+回溯

由于每一个位置都有可能是搜索的起点，对于每一个搜索的位置来说，用DFS递归查找需要的路径。
先定义递归DFS函数：
find(){
第一步,递归出口
第二步，检查元素是否被访问过``<br />
第三步，都没有返回，继续递归
find()
回溯
}

public boolean find(char[][] array, int rows, int cols, int row, int col, char[] str, int str_pos, boolean isVisited[][]){
    //递归出口条件
    //当 row<0 || row>=rows || col<0 || col>=cols || isVisited[row][col] || array[row][col] != str[str_pos] 满足任意一条返回 false,说明此路不通;
    //当 str_pos == str.length 返回 true, 表示数组中有这条路径，递归结束;
    if(row<0 || row>=rows || col<0 || col>=cols || isVisited[row][col] || array[row][col] != str[str_pos])
        return false;
    if(str_pos == str.length)
        return true;
    //标记这个位置已经被访问过了
    isVisited[row][col] = true;
    //程序能走到这里说明当前位置没有越界，并且array[row][col] == str[str_pos],这样就可以继续往下搜索了
    boolean result = find(array, rows, cols, row-1, col, str, str_pos+1, isVisited)
                  || find(array, rows, cols, row, col+1, str, str_pos+1, isVisited)
                  || find(array, rows, cols, row+1, col, str, str_pos+1, isVisited)
                  || find(array, rows, cols, row, col-1, str, str_pos+1, isVisited);
    //非常重要的一步:回溯. 如果不回溯的话，假设某一次递归时,访问到当前位置设为(x,y), 但是此路不通，
    //也就是说这条路径搜索不到我们想要的字符串。这时，所有的递归都不能访问该位置,程序就是错的
    isVisited[row][col] = false;
    return result;
}
//输入的是一维字符数组,转成二维数组,容易理解
public boolean hasPath(char[] matrix, int rows, int cols, char[] str) {
      visit = new int[rows][cols];
      char[][] array = new char[rows][cols];
      for (int i = 0; i < rows ; i++) {
          for(int j = 0; j < cols; j++) {
              array[i][j] = matrix[i*cols + j];
          }
      }
        for (int i = 0; i < rows ; i++) {
            for(int j = 0; j < cols; j++) {
               if(find(array,rows,cols,str,i,j,0)){
                   return  true;
               }
            }
        }
      return false;
}