1. result = []
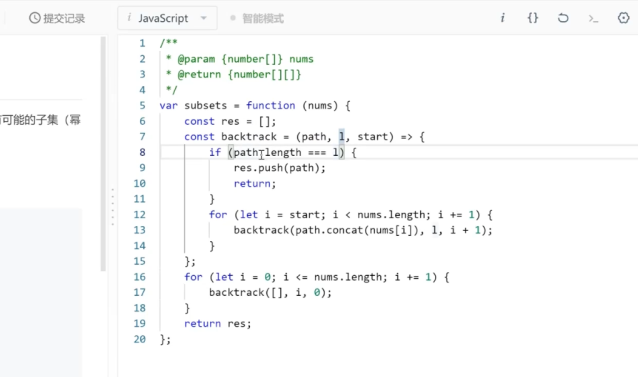
  2. def backtrack(路径, 选择列表):
  3.     if 满足结束条件:
  4.         result.add(路径)
  5.         return
  7.     for 选择 in 选择列表:
  8.         做选择
  9.         backtrack(路径, 选择列表)
  10.         撤销选择

其核心就是 for 循环里面的递归，在递归调用之前「做选择」，在递归调用之后「撤销选择」，特别简单。

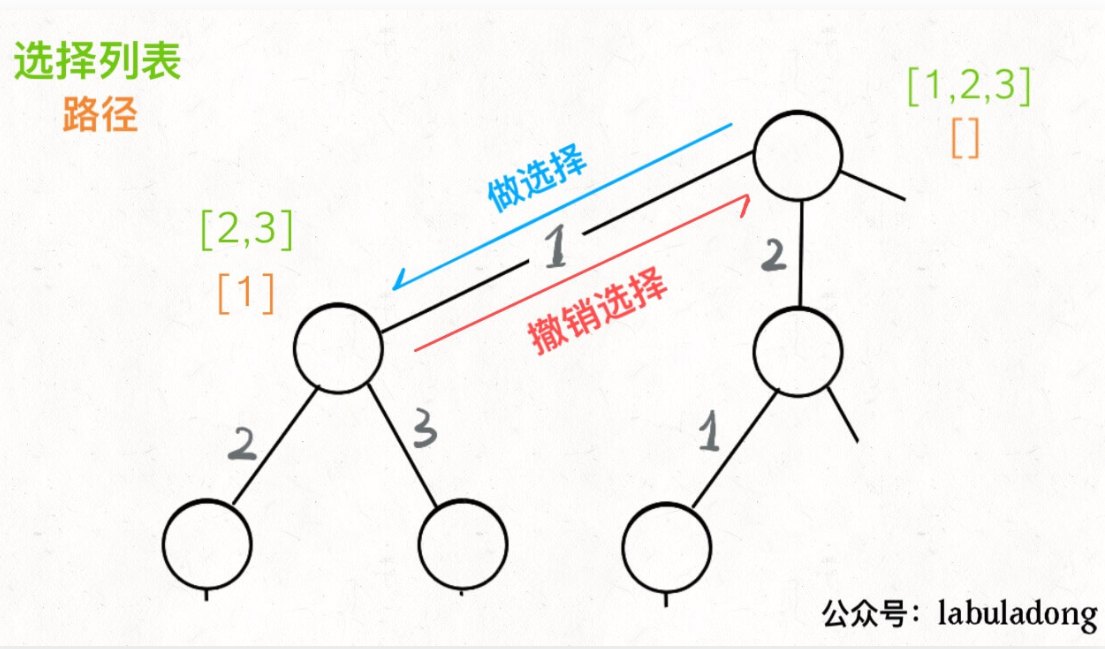
image.png
image.png
回溯就是终止递归

46. 全排列

给定一个不含重复数字的数组nums，返回其所有可能的全排列。你可以按任意顺序返回答案。 输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

  1. var permute = function(nums) {
  2.     const list = [];
  3.     backtrack(list, [], nums)
  4.     return list
  5. };
  7. function backtrack(list, track, nums) {
  8.     if (track.length === nums.length) {
  9.         list.push([...track]);
  10.         return
  11.     } 
  12.     for(let i = 0; i < nums.length; i++) {
  13.         if (track.includes(nums[i])) continue;
  14.         track.push(nums[i]);
  15.         backtrack(list, track, nums);
  16.         track.pop();
  17.     }
  18. }

51. N 皇后

n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。 给你一个整数 n ，返回所有不同的 n 皇后问题 的解决方案。

每一种解法包含一个不同的 n 皇后问题 的棋子放置方案，该方案中 ‘Q’ 和 ‘.’ 分别代表了皇后和空位。

输入：n = 4输出：[[“.Q..”,”…Q”,”Q…”,”..Q.”],[“..Q.”,”Q…”,”…Q”,”.Q..”]] 解释：如上图所示，4 皇后问题存在两个不同的解法。

image.png