递归模板

/* 二叉树遍历框架 */
void traverse(TreeNode root) {
    if (root == null) {
        return;
    }
    // 前序位置
    traverse(root.left);
    // 中序位置
    traverse(root.right);
    // 后序位置
}

前中后序是遍历二叉树过程中处理每一个节点的三个特殊时间点

• 前序位置的代码在刚刚进入一个二叉树节点的时候执行；
• 后序位置的代码在将要离开一个二叉树节点的时候执行；
• 中序位置的代码在一个二叉树节点左子树都遍历完，即将开始遍历右子树的时候执行。

• 二叉树深度优先遍历
  • 前序遍历： 144.二叉树的前序遍历
  • 后序遍历： 145.二叉树的后序遍历
  • 中序遍历： 94.二叉树的中序遍历
• 二叉树广度优先遍历
  • 层序遍历：102.二叉树的层序遍历

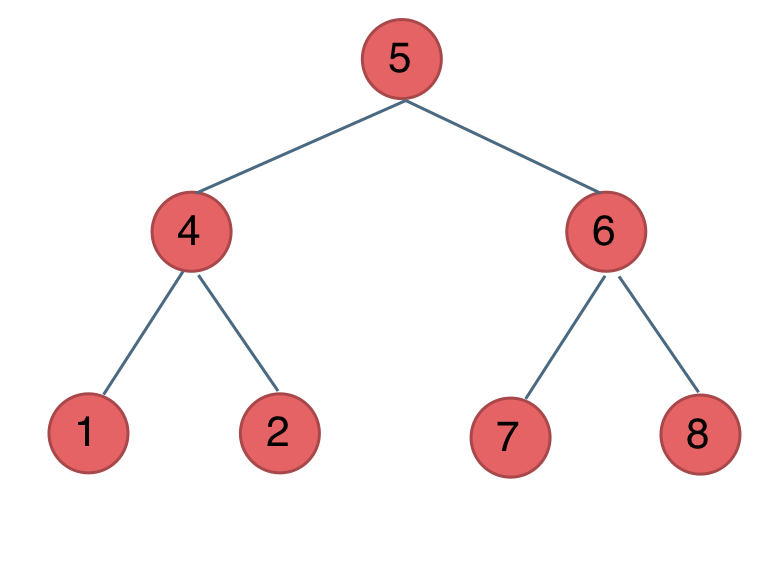
前中后序遍历顺序如下：

• 前序遍历（中左右）：5 4 1 2 6 7 8
• 中序遍历（左中右）：1 4 2 5 7 6 8
• 后序遍历（左右中）：1 2 4 7 8 6 5 ```javascript

var preorderTraversal = (root) => { let result = [] var preOrderTraverseNode = (node) => { if(node) { // 前序遍历 result.push(node.val) preOrderTraverseNode(node.left) preOrderTraverseNode(node.right) } } preOrderTraverseNode(root) return result };

> **写递归算法的关键是要明确函数的「定义」是什么，然后相信这个定义，利用这个定义推导最终结果，绝不要试图跳入递归**。

```javascript
// 定义：count(root) 返回以 root 为根的树有多少节点
int count(TreeNode root) {
    // base case
    if (root == null) return 0;
    // 自己加上子树的节点数就是整棵树的节点数
    return 1 + count(root.left) + count(root.right);
}

写树相关的算法，简单说就是，先搞清楚当前root节点该做什么，然后根据函数定义递归调用子节点，递归调用会让孩子节点做相同的事情。
二叉树题目的一个难点就是，如何把题目的要求细化成每个节点需要做的事情。

tips

• 只有后序位置才能通过返回值获取子树的信息。那么换句话说，一旦你发现题目和子树有关，那大概率要给函数设置合理的定义和返回值，在后序位置写代码了。

  226

  226. 翻转二叉树

  翻转一棵二叉树

var invertTree = function (root) {
    if (root === null) {
        return null;
    }
      //交换根节点的左右子树
    const temp = root.left;
    root.left = root.right;
    root.right = temp;
    invertTree(root.left);
    invertTree(root.right);
    return root;
};

116

116. 填充每个节点的下一个右侧节点指针

给定一个 完美二叉树 ，其所有叶子节点都在同一层，每个父节点都有两个子节点。二叉树定义如下：

struct Node { int val; Node left; Node right; Node *next; } 填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL。

初始状态下，所有 next 指针都被设置为 NULL。

进阶：

• 你只能使用常量级额外空间。
• 使用递归解题也符合要求，本题中递归程序占用的栈空间不算做额外的空间复杂度。

输入：root = [1,2,3,4,5,6,7]输 输出：[1,#,2,3,#,4,5,6,7,#] 解释：给定二叉树如图 A 所示，你的函数应该填充它的每个 next 指针，以指向其下一个右侧节点，如图 B 所示。序列化的输出按层序遍历排列，同一层节点由 next 指针连接，’#’ 标志着每一层的结束。

/**
 * // Definition for a Node.
 * function Node(val, left, right, next) {
 *    this.val = val === undefined ? null : val;
 *    this.left = left === undefined ? null : left;
 *    this.right = right === undefined ? null : right;
 *    this.next = next === undefined ? null : next;
 * };
 */

/**
 * @param {Node} root
 * @return {Node}
 */
var connect = function (root) {
    if (root == null) return null;
    connectNode(root.left, root.right);
    return root;
};

var connectNode = function (node1, node2) {
    if (node1 == null || node2 == null) {
        return;
    }
    /**** 前序遍历位置 ****/
    // 将传入的两个节点连接
    node1.next = node2;

    // 连接相同父节点的两个子节点
    connectNode(node1.left, node1.right);
    connectNode(node2.left, node2.right);
    // 连接跨越父节点的两个子节点
    connectNode(node1.right, node2.left);
}

另一种方法:

var connect = function (root) {
    if (root == null) return null;
    // connectNode(root.left, root.right);
    dfs(root);
    return root;
};

var dfs = function (node, next) {
    if (node != null) {
        node.next = next;
        dfs(node.left, node.right);
        dfs(node.right, node.next ? node.next.left : null)
    }

}

备注：有点玄学，二叉树的递归需要加深理解

114

114. 二叉树展开为链表

给你二叉树的根结点 root ，请你将它展开为一个单链表： 展开后的单链表应该同样使用 TreeNode ，其中 right 子指针指向链表中下一个结点，而左子指针始终为 null 。 展开后的单链表应该与二叉树 先序遍历 顺序相同。

var flatten = function (root) {
    if (!root) return null;
    flatten(root.left);
    flatten(root.right);

    // 1、左右子树已经被拉平成一条链表
    const left = root.left;
    const right = root.right;

    // 2、将左子树作为右子树
    root.left = null;
    root.right = left


    // 3、将原先的右子树接到当前右子树的末端
    while (root.right) {
        root = root.right
    }
    root.right = right
};

另一种做法：

var flatten = function(root) {
    const list = [];
    preorderTraversal(root, list);
    const size = list.length;
    for (let i = 1; i < size; i++) {
        const prev = list[i - 1], curr = list[i];
        prev.left = null;
        prev.right = curr;
    }
};

const preorderTraversal = (root, list) => {
    if (root != null) {
       //前序遍历
        list.push(root);
        preorderTraversal(root.left, list);
        preorderTraversal(root.right, list);
    }
}

参考：