1、贝塞尔曲线简介

贝塞尔曲线的本质是通过数学公式的计算绘制出一条平滑的曲线。

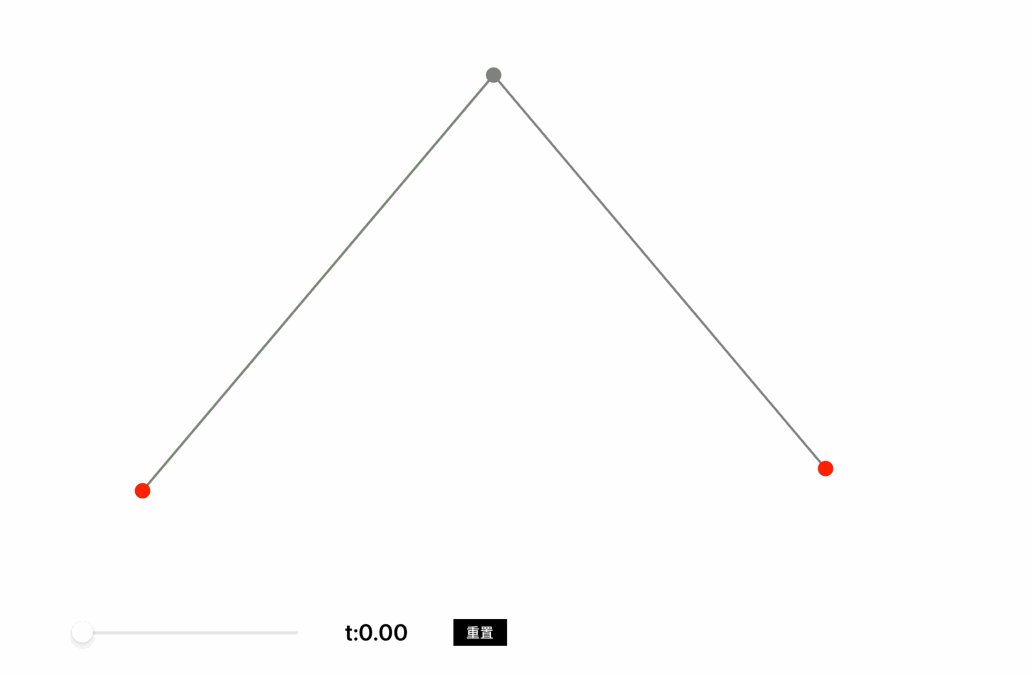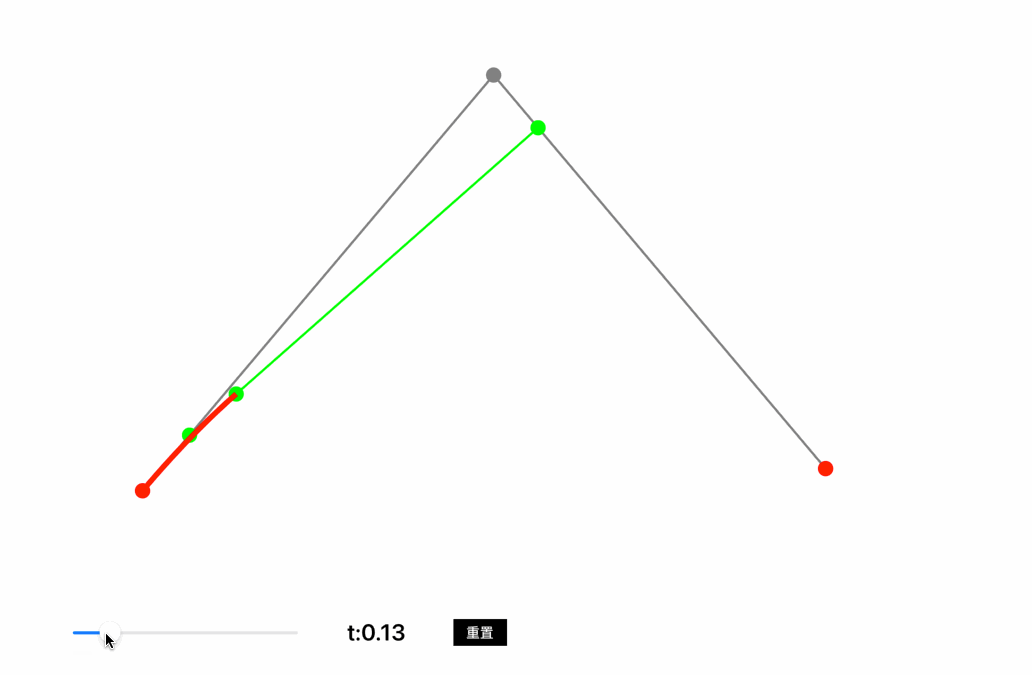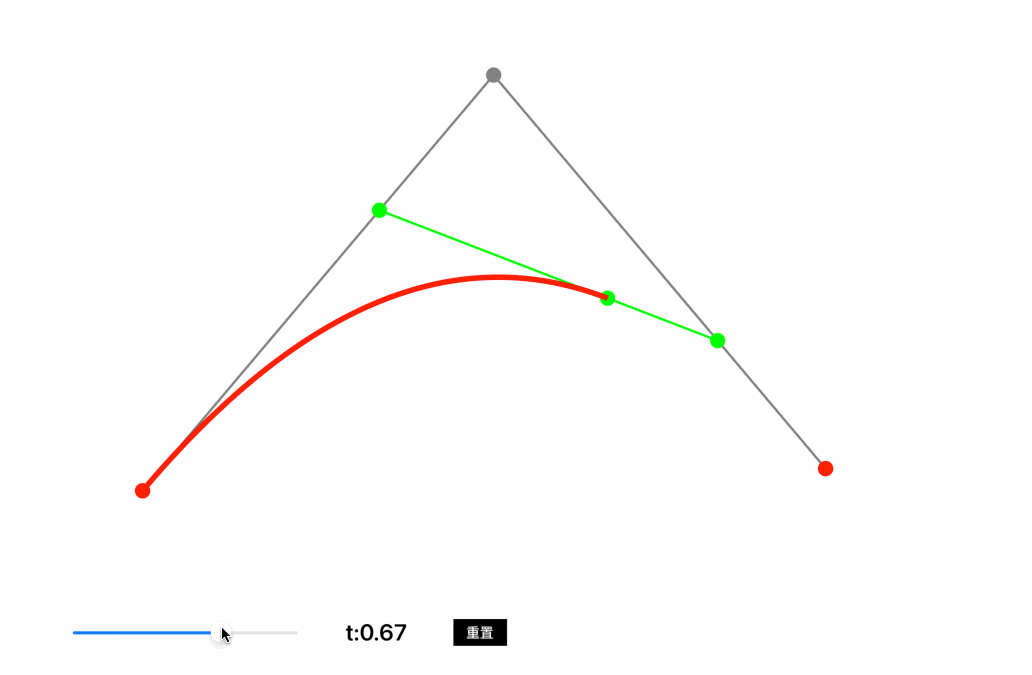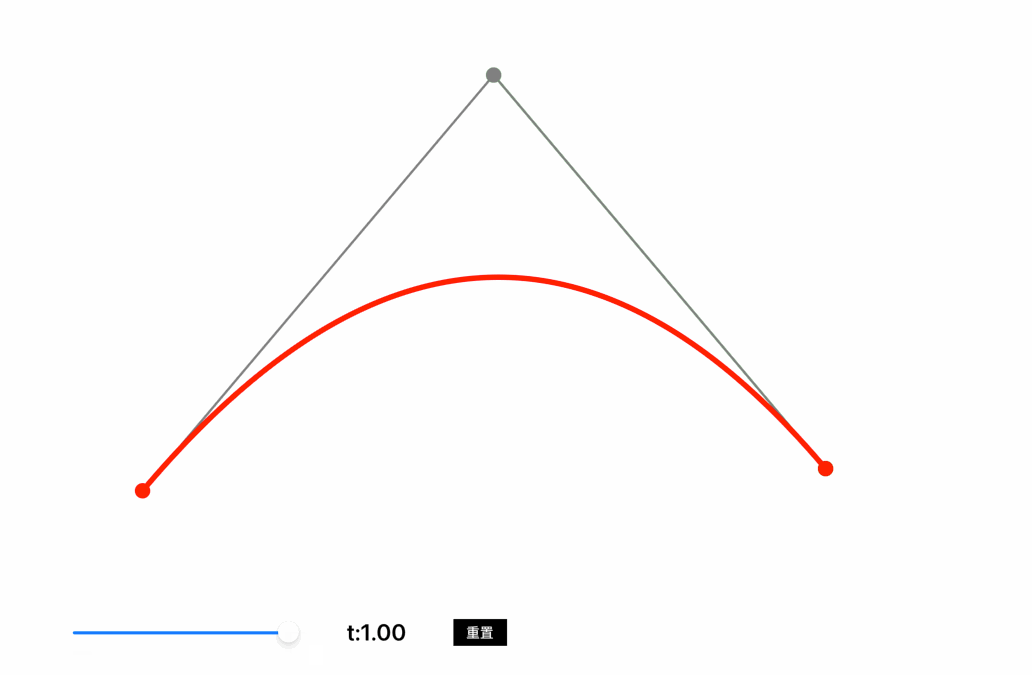
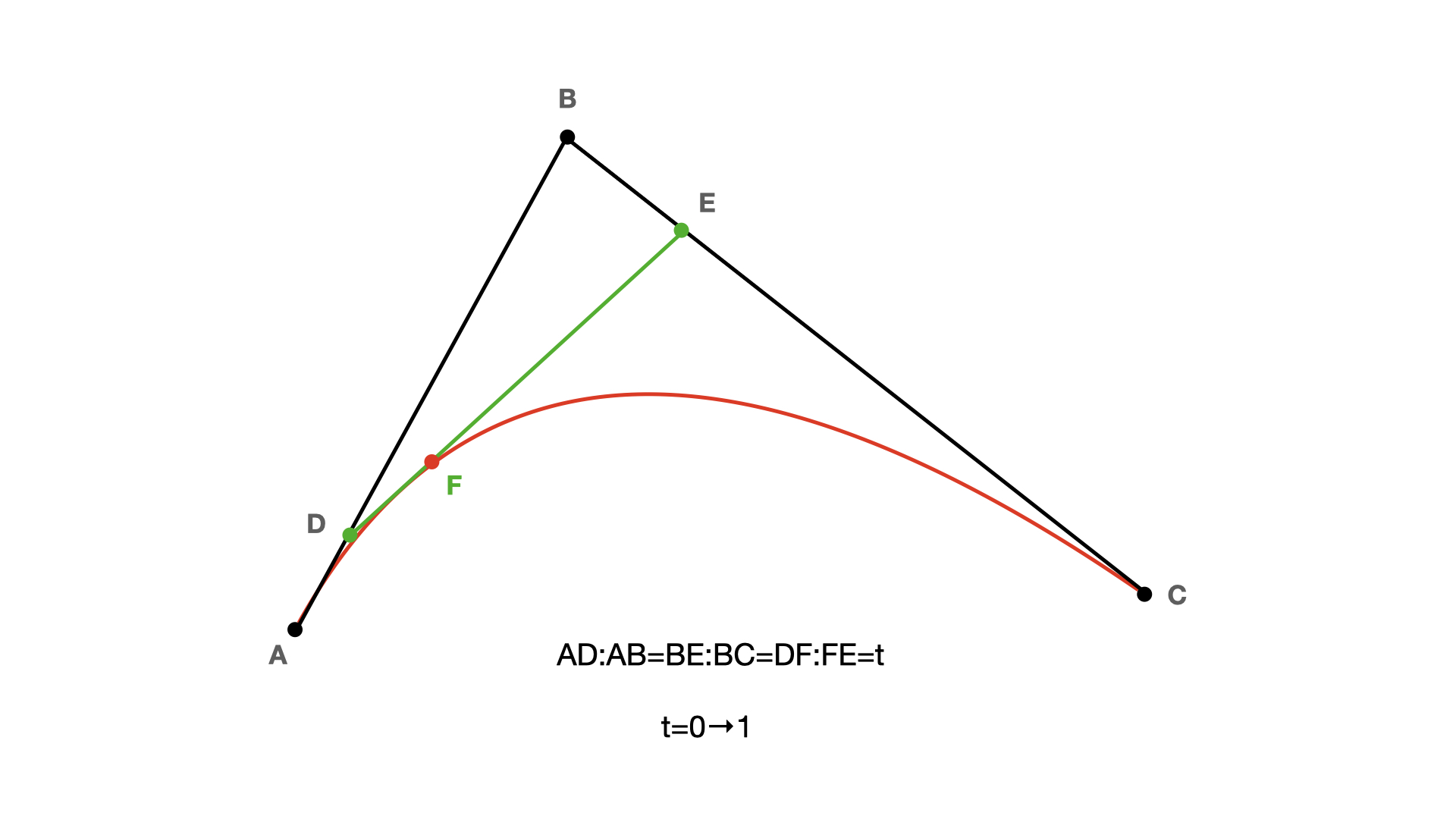
玩转贝塞尔曲线 - 图1 玩转贝塞尔曲线 - 图2

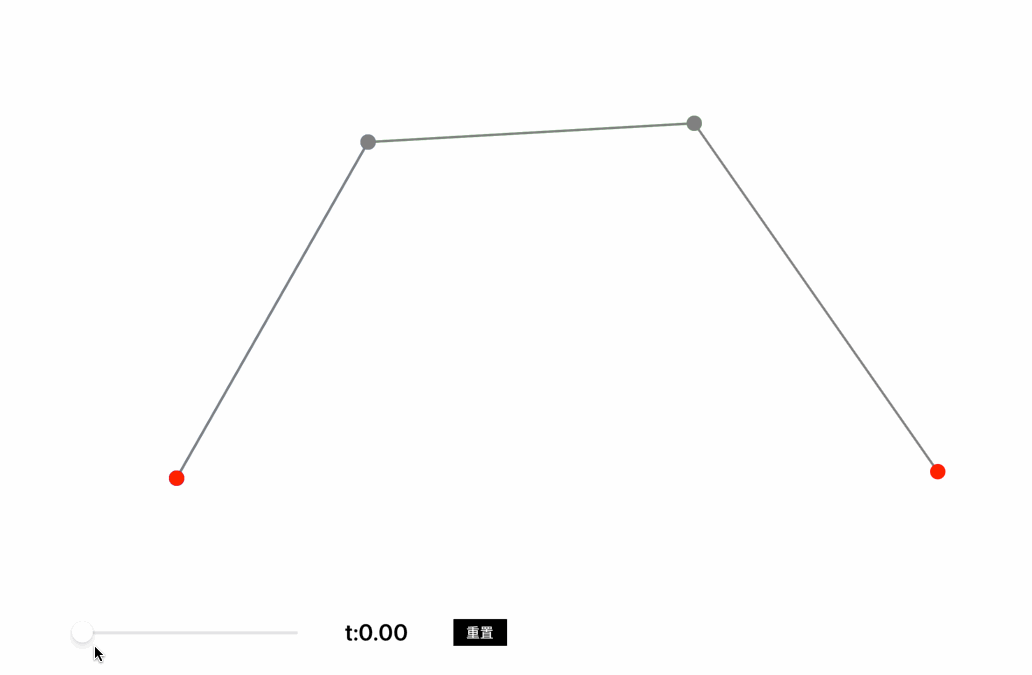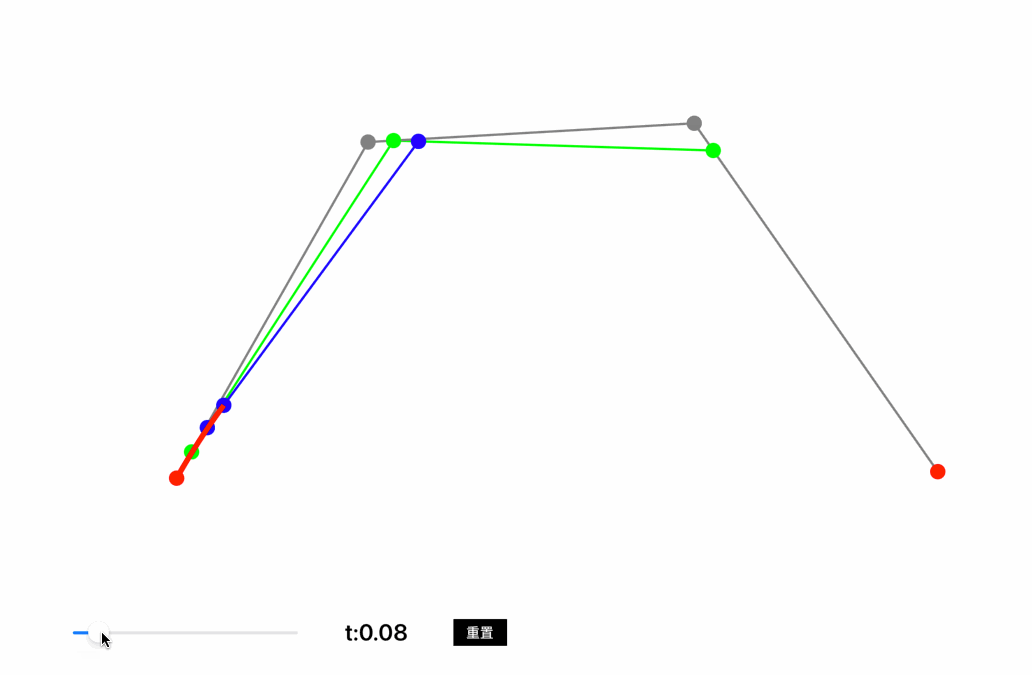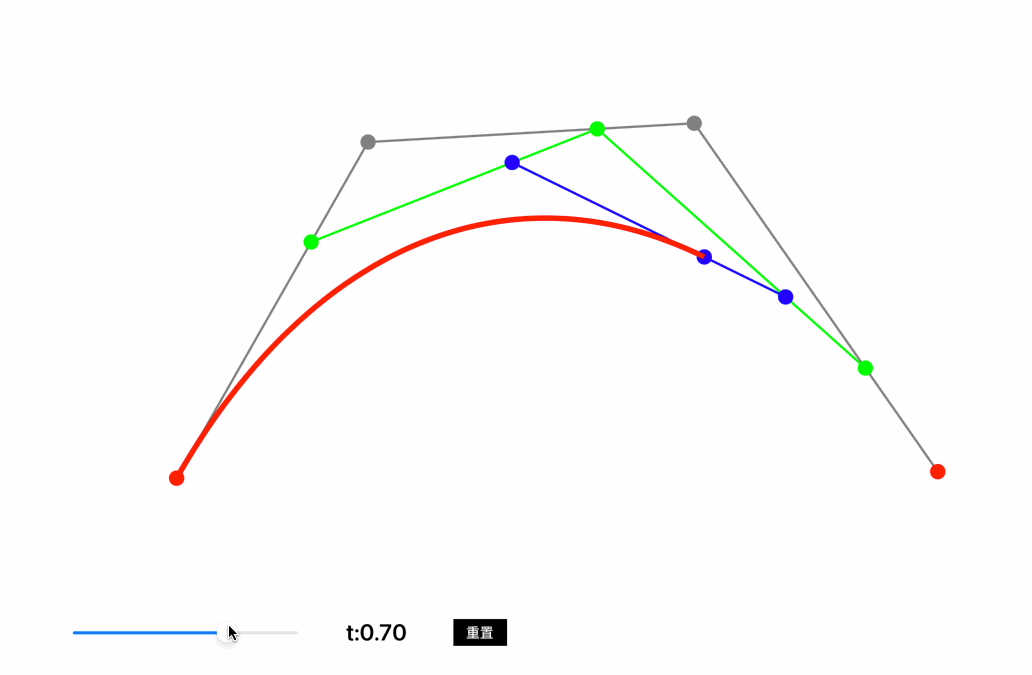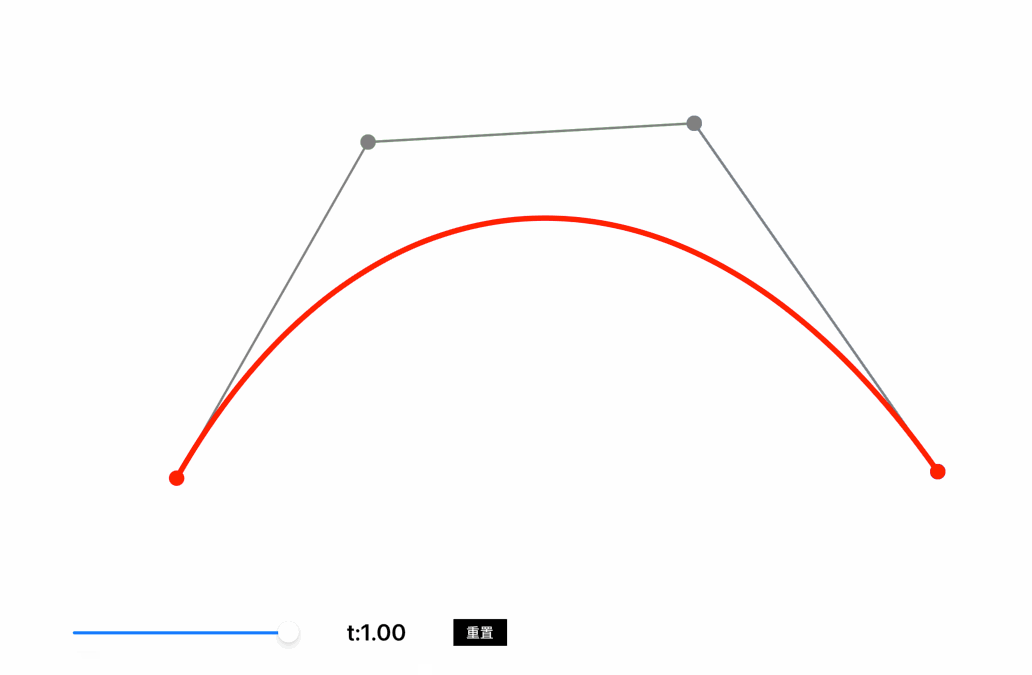
从A向C绘制一条贝塞尔曲线，控制点为B，在线段AB中取点D，在线段BC中取点E，在DE线段中取点F，保证AD:AB=BE:BC=DF:DE，则F点移动的轨迹就是A点到C点的贝塞尔曲线，也称作二阶贝塞尔曲线。

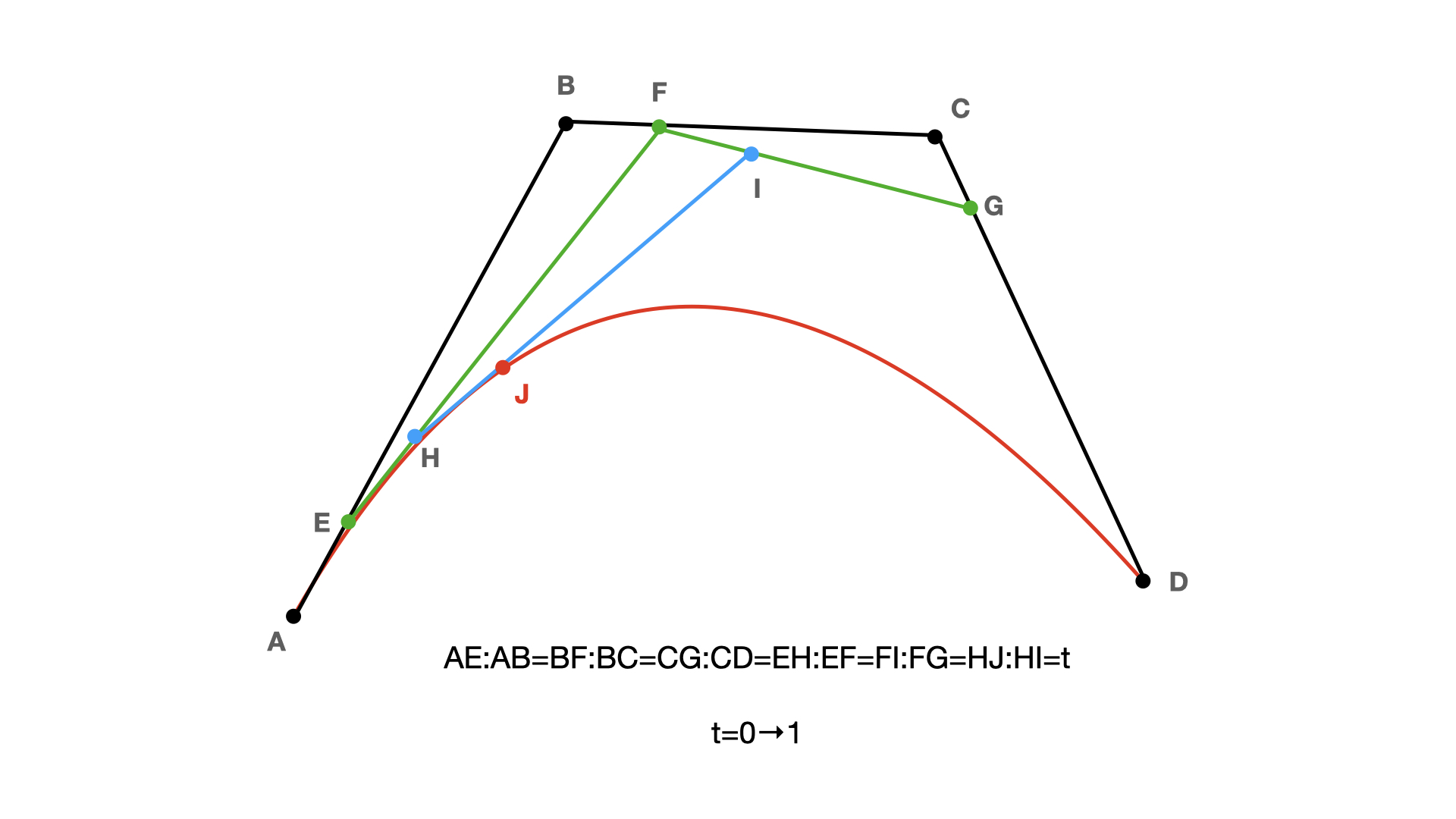
玩转贝塞尔曲线 - 图3 玩转贝塞尔曲线 - 图4

三阶贝塞尔曲线：从A点向D点绘制一条贝塞尔曲线，控制点为B和C，在线段AB取点E，线段BC取点F，线段CD取点G，线段EF取点H，线段FG取点I，线段HI取点J，保证AE:AB=BF:BC=CG:CD=EH:EF=FI:FG=HJ:HI，则J点移动的轨迹就是从点A到点D的三阶贝塞尔曲线。
高阶贝塞尔曲线以此类推，由多个控制点来绘制曲线。

2、贝塞尔曲线绘制

2.1 绘制图形

iOS系统提供了一些绘制指定图形的方法：

  1. //在指定区域内绘制矩形 
  2. + (instancetype)bezierPathWithRect:(CGRect)rect; 
  3. //在指定区域内绘制圆形（椭圆、正圆）
  4. + (instancetype)bezierPathWithOvalInRect:(CGRect)rect; 
  5. //绘制带圆角的矩形 
  6. + (instancetype)bezierPathWithRoundedRect:(CGRect)rect cornerRadius:(CGFloat)cornerRadius;  
  7. + (instancetype)bezierPathWithRoundedRect:(CGRect)rect byRoundingCorners:(UIRectCorner)corners cornerRadii:(CGSize)cornerRadii; 
  8. //绘制圆弧 
  9. + (instancetype)bezierPathWithArcCenter:(CGPoint)center radius:(CGFloat)radius startAngle:(CGFloat)startAngle endAngle:(CGFloat)endAngle clockwise:(BOOL)clockwise;

也有自定义添加曲线的方法:

  1. //向指定点添加一条直线
  2. - (void)addLineToPoint:(CGPoint)point;
  3. //向指定点添加一条二阶曲线
  4. - (void)addQuadCurveToPoint:(CGPoint)endPoint controlPoint:(CGPoint)controlPoint;
  5. //向指定点添加一条三阶曲线
  6. - (void)addCurveToPoint:(CGPoint)endPoint controlPoint1:(CGPoint)controlPoint1 controlPoint2:(CGPoint)controlPoint2;
  7. //添加一段圆弧
  8. - (void)addArcWithCenter:(CGPoint)center radius:(CGFloat)radius startAngle:(CGFloat)startAngle endAngle:(CGFloat)endAngle clockwise:(BOOL)clockwise API_AVAILABLE(ios(4.0));

贝塞尔曲线只是一条曲线，如果想让曲线在屏幕上渲染，需要和CAShapeLayer(图层)配合使用，曲线用于制定路径，图层负责绘制曲线。

  1. //创建一个曲线
  2. UIBezierPath *path = [UIBezierPath bezierPath];
  3. //创建一个图层
  4. CAShapeLayer *layer = [CAShapeLayer layer];
  5. layer.path = path.CGPath;

以矩形为例，有两种绘制方式：
方法一：使用由系统方法，在指定区域内绘制一个矩形；
方法二：从A到B、B到C、C到D、D到A分别绘制的四条边，组成一个完整的矩形。
其它图形的绘制方法大同小异，或者使用系统提供的绘制特定图形的方法，或者利用一些特定的数学公式进行计算得到各个点进行绘制。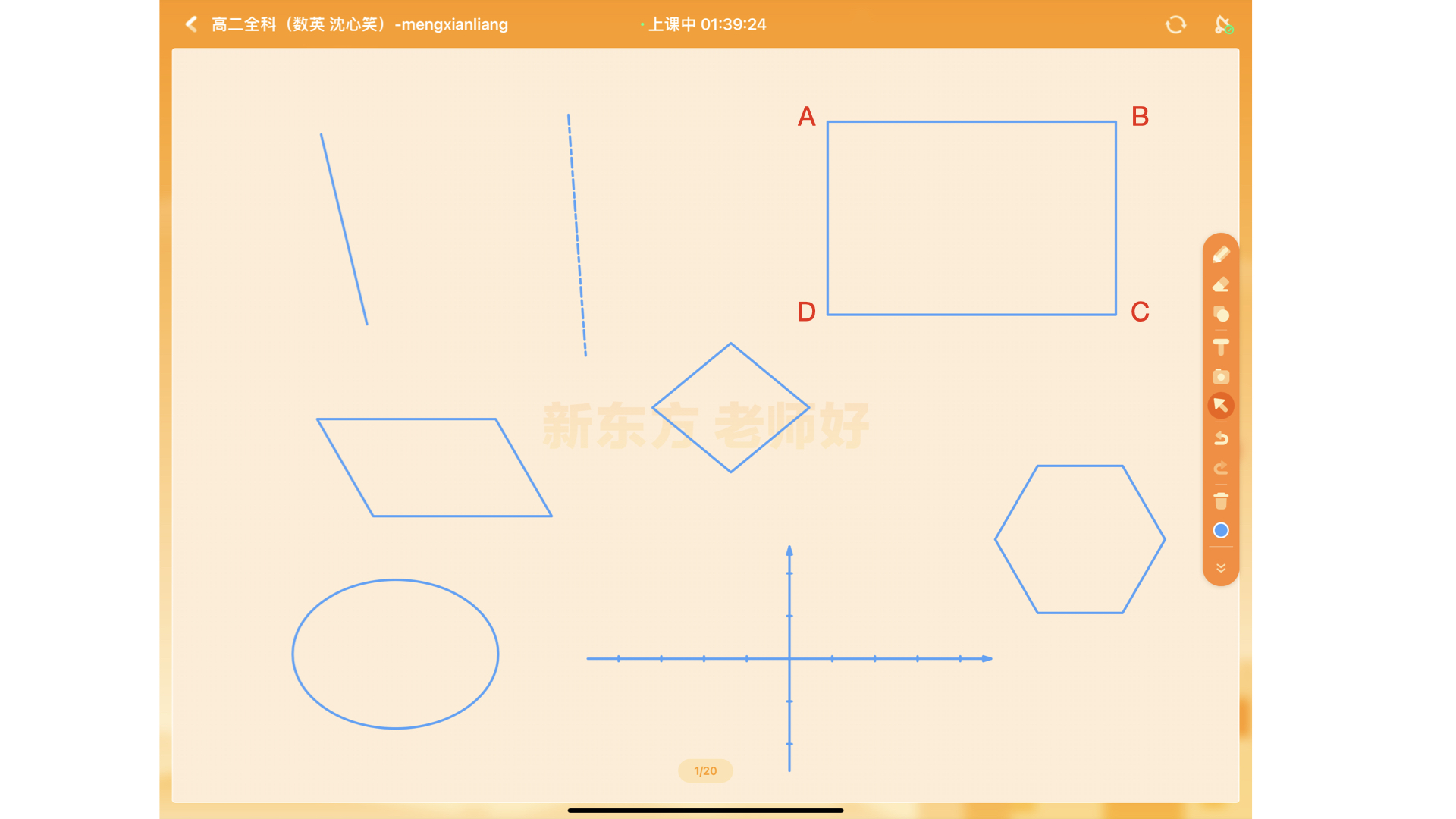
玩转贝塞尔曲线 - 图5

2.2 绘制画笔

与图形绘制不同，画笔绘制没有固定的公式，是由手指(鼠标)在屏幕上滑动时取到多个点连接而成的轨迹。所以书笔记可以用增量的方式绘制，如下图所示，手指在屏幕上从左向右滑动，当移动到的新的点B时，只绘制了上一点A和B之间的部分曲线，也就是说手指在屏幕上每捕获一个新的点只需要绘制两点间的曲线。所以笔记绘制时的性能消耗是比较小的，教室内多人同时书写也不会卡顿。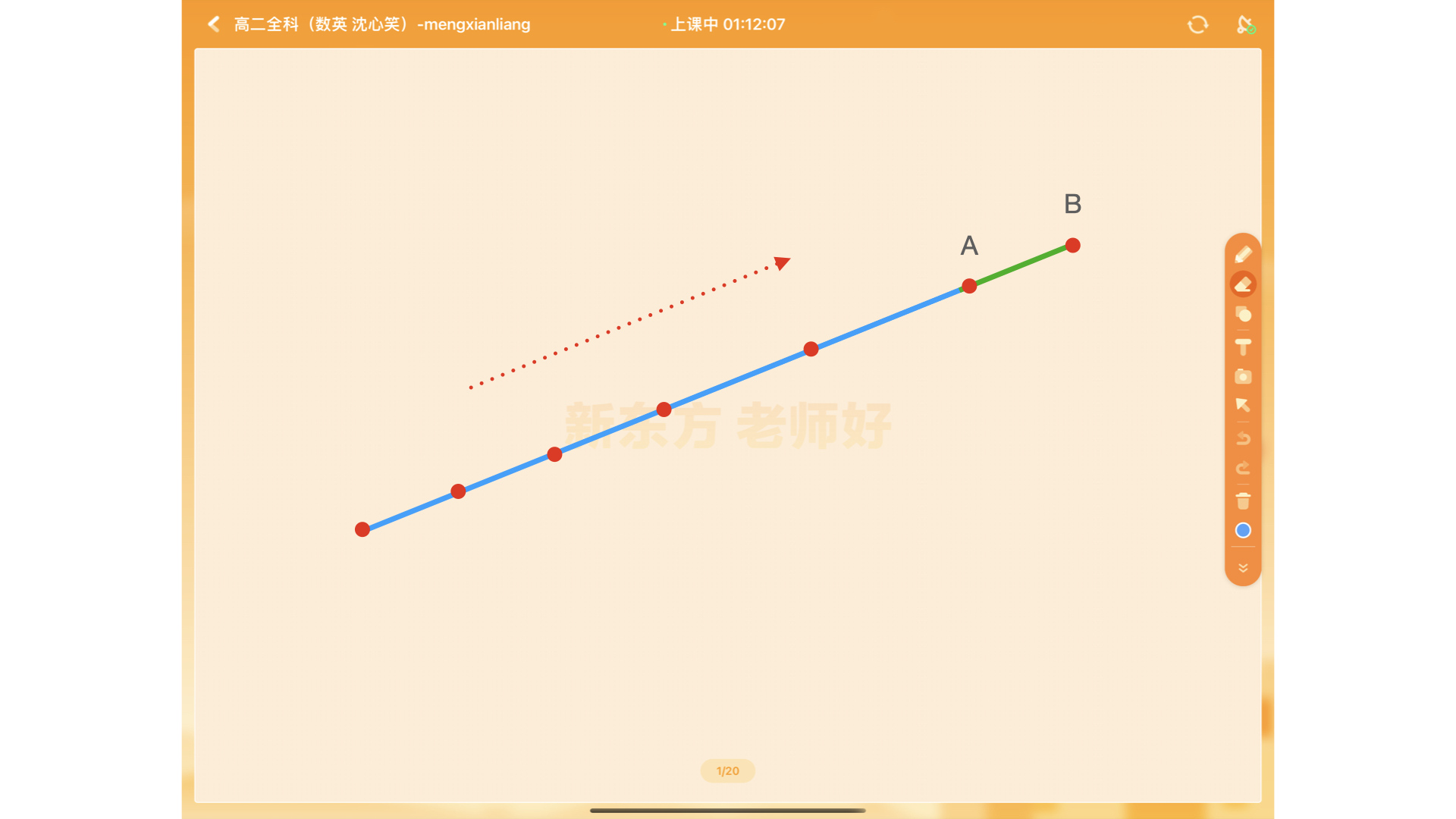
玩转贝塞尔曲线 - 图6

2.3 绘制圆弧

2.3.1 圆弧坐标系

  1. //绘制圆弧 
  2. + (instancetype)bezierPathWithArcCenter:(CGPoint)center radius:(CGFloat)radius startAngle:(CGFloat)startAngle endAngle:(CGFloat)endAngle clockwise:(BOOL)clockwise;

绘制圆弧坐标系如下：
玩转贝塞尔曲线 - 图7

2.3.2 实现圆环进度指示器

玩转贝塞尔曲线 - 图8
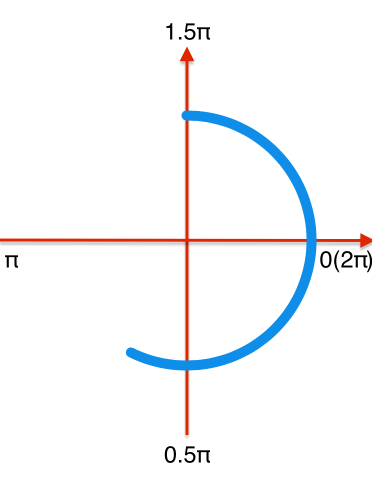
实现如上图所示的圆环进度条，需要绘制一条从-0.5π到1.5π的顺时针圆环，通过CAShapeLayer显示。

  1. //创建一个完整的圆形
  2. UIBezierPath *path = [UIBezierPath bezierPathWithArcCenter:CenterPoint startAngle:-0.5f*M_PI endAngle:1.5f*M_PI clockwise:YES];
  3. //创建一个图层
  4. CAShapeLayer *layer = [CAShapeLayer layer];
  5. layer.path = path.CGPath;

layer有两个属性strokeStart(起点值)和strokeEnd(终点值)，取值范围0-1，strokeStart默认为0，strokeEnd默认为1。设置这两个属性可以让layer展示path指定的一部分。进度条默认将strokeEnd设置为0，接收到进度更新时，将layer的strokeEnd属性设置为下载的百分比，就得到了圆形进度条的效果。

2.3.3 支付宝支付中效果

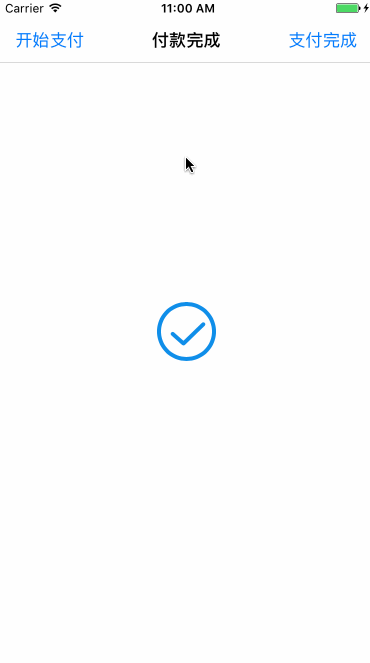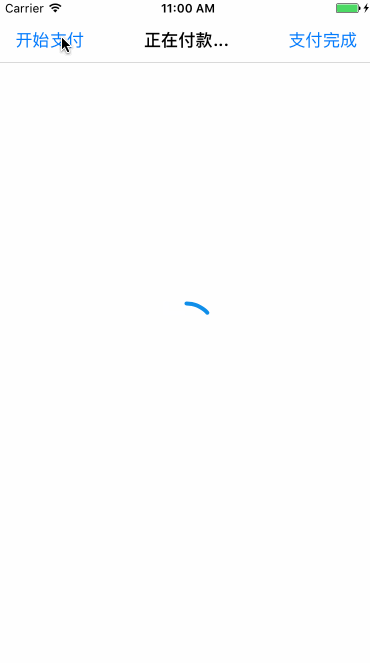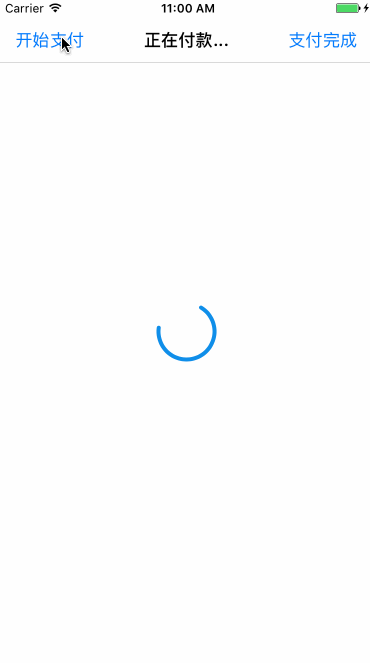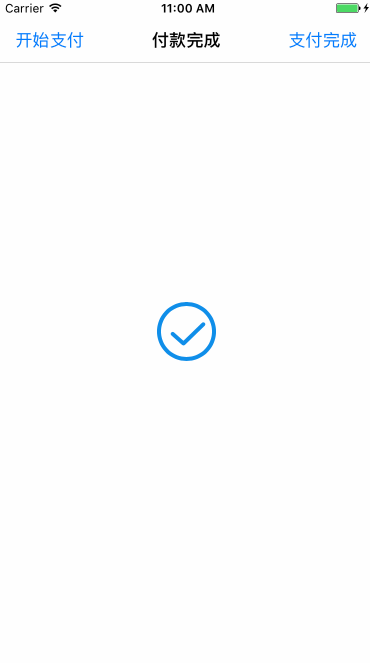
玩转贝塞尔曲线 - 图9
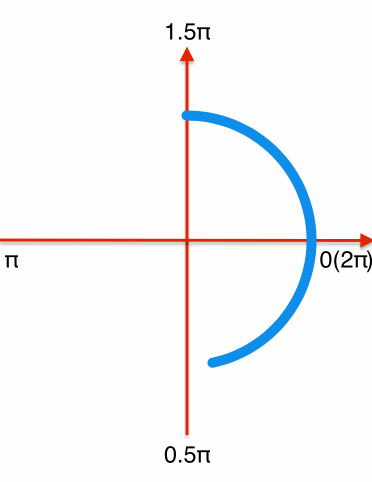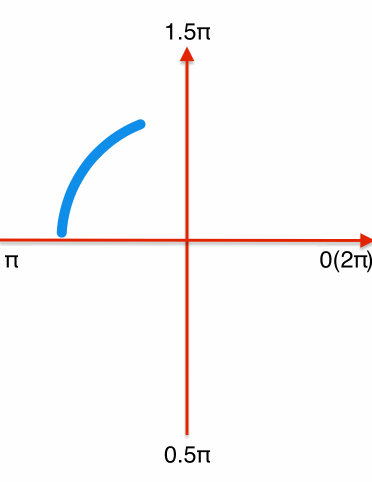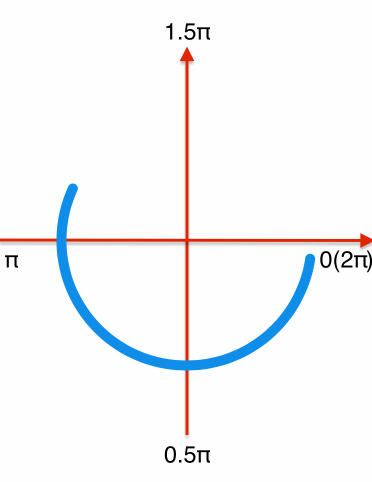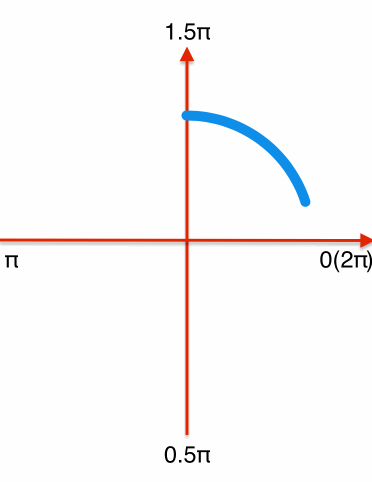
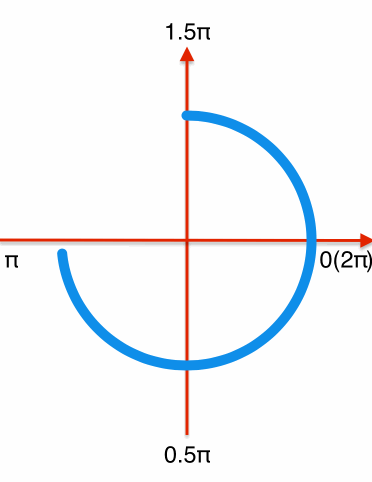
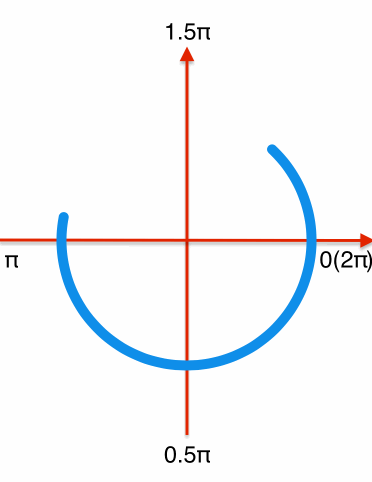
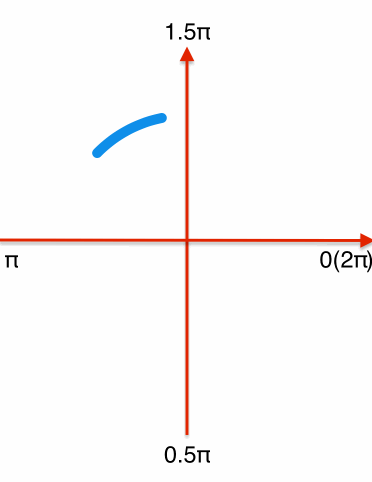
和绘制圆环进度条相同，首先绘制一个从-0.5π到1.5π的顺时针圆环，需要特定的时机更新layer的strokeEnd和strokeStart，分解效果如下：

玩转贝塞尔曲线 - 图10 玩转贝塞尔曲线 - 图11 玩转贝塞尔曲线 - 图12 玩转贝塞尔曲线 - 图13 玩转贝塞尔曲线 - 图14

一个循环过程可分解为前后两段：
前半段：从0到0.75匀速更新圆环的strokeEnd（即圆环完成-0.5π到π的绘制），此过程中strokeStart保持不变。
后半段：strokeEnd从0.75开始速度变慢，逐渐增加到1。在这个过程中strokeStart以strokeEnd4倍的速度从0变化到1（弧度从-0.5π到1.5π），在角度为1.5π时，strokeStart追上strokeEnd都变化到1，完成一个循环过程。
下个循环开始时将strokeEnd和strokeStart设置为0，重复上面的逻辑。

2.4 曲线拼接

iOS系统提供了曲线拼接的方法，path可以拼接其它的path对象。

  1. //拼接曲线
  2. - (void)appendPath:(UIBezierPath *)bezierPath;

下面以删除笔记为例，讲一下曲线拼接的在魔法课堂中的应用，系统中提供了区域包含点的方法：

  1. CG_EXTERN bool CGPathContainsPoint(CGPathRef cg_nullable path,
  2.     const CGAffineTransform * __nullable m, CGPoint point, bool eoFill)
  3.     CG_AVAILABLE_STARTING(10.4, 2.0);

笔记删除也是围绕区域和点进行匹配的原则实现的，橡皮擦作为一个点，但是笔记是通过贝塞尔曲线进行绘制的，点无法和线进行匹配，所以给笔记添加了扩展区域来辅助计算，调节橡皮擦大小本质是在调解扩展区域大小，扩展区域有前后两个版本：
老版本：遍历曲线中的每个点，取前一个点生成两个辅助点A、B，后一个点生成两个辅助点C、D，生成一个闭合的平行四边形ABCD，这样笔记的路径上就出现了多个平行四边行，当橡皮擦在屏幕上移动时，通过橡皮擦的点和扩展平行四边行就行匹配，来计算待删除笔记。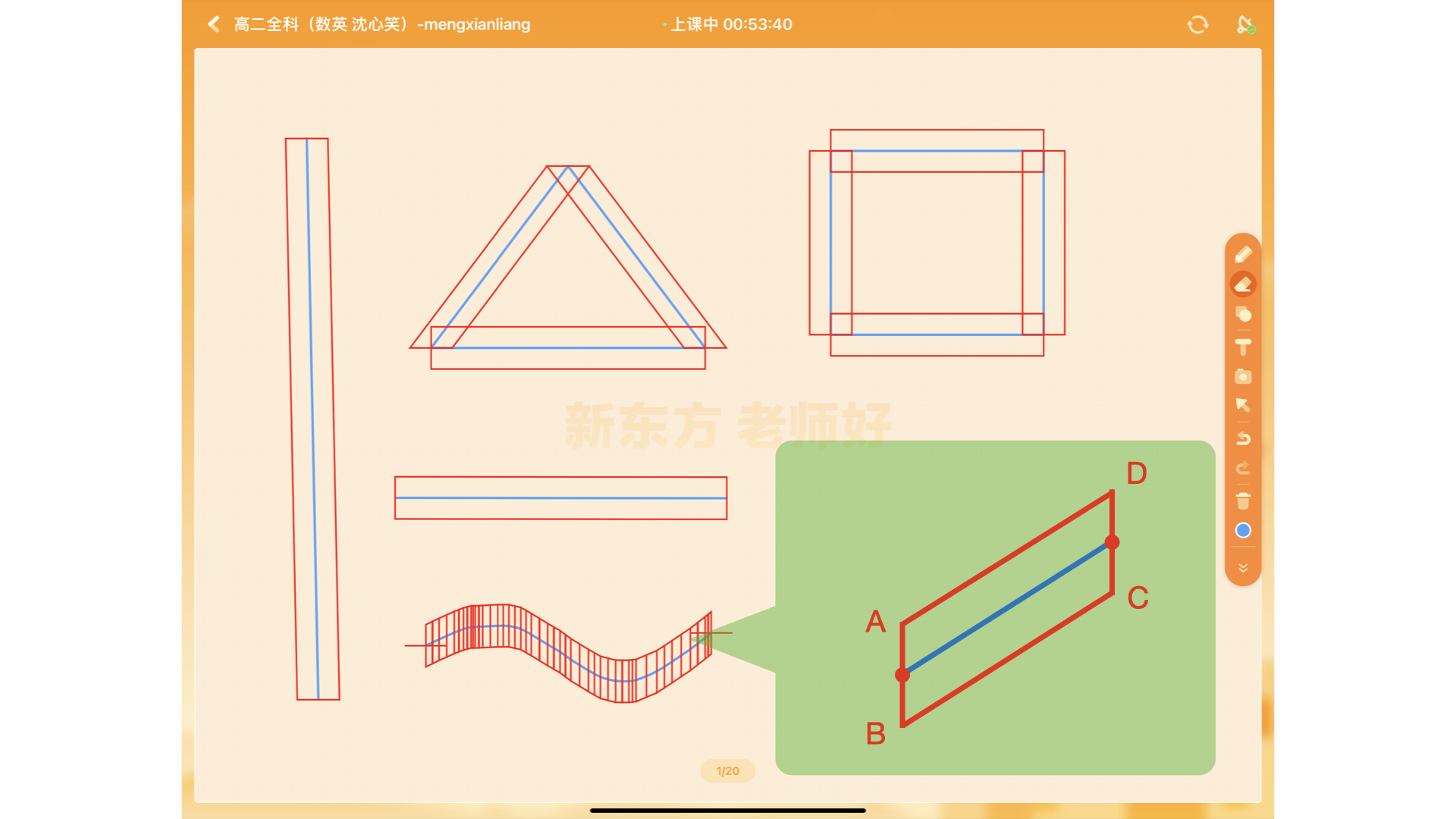
玩转贝塞尔曲线 - 图15

不足：如果笔记点中的点比较多，生成小的四边行较多，计算量会比较大。其次笔记末端匹配准确。
新版本：设笔记绘制方向为正向，将正向方向所有左侧和右侧点各自绘制出一条曲线，两个末端绘制两条曲线，将四条曲线拼接成一个完整的扩展区域。这种方式可以保证橡皮擦移动时每条笔记只需计算一个扩展区域，并提高笔记末端计算精度。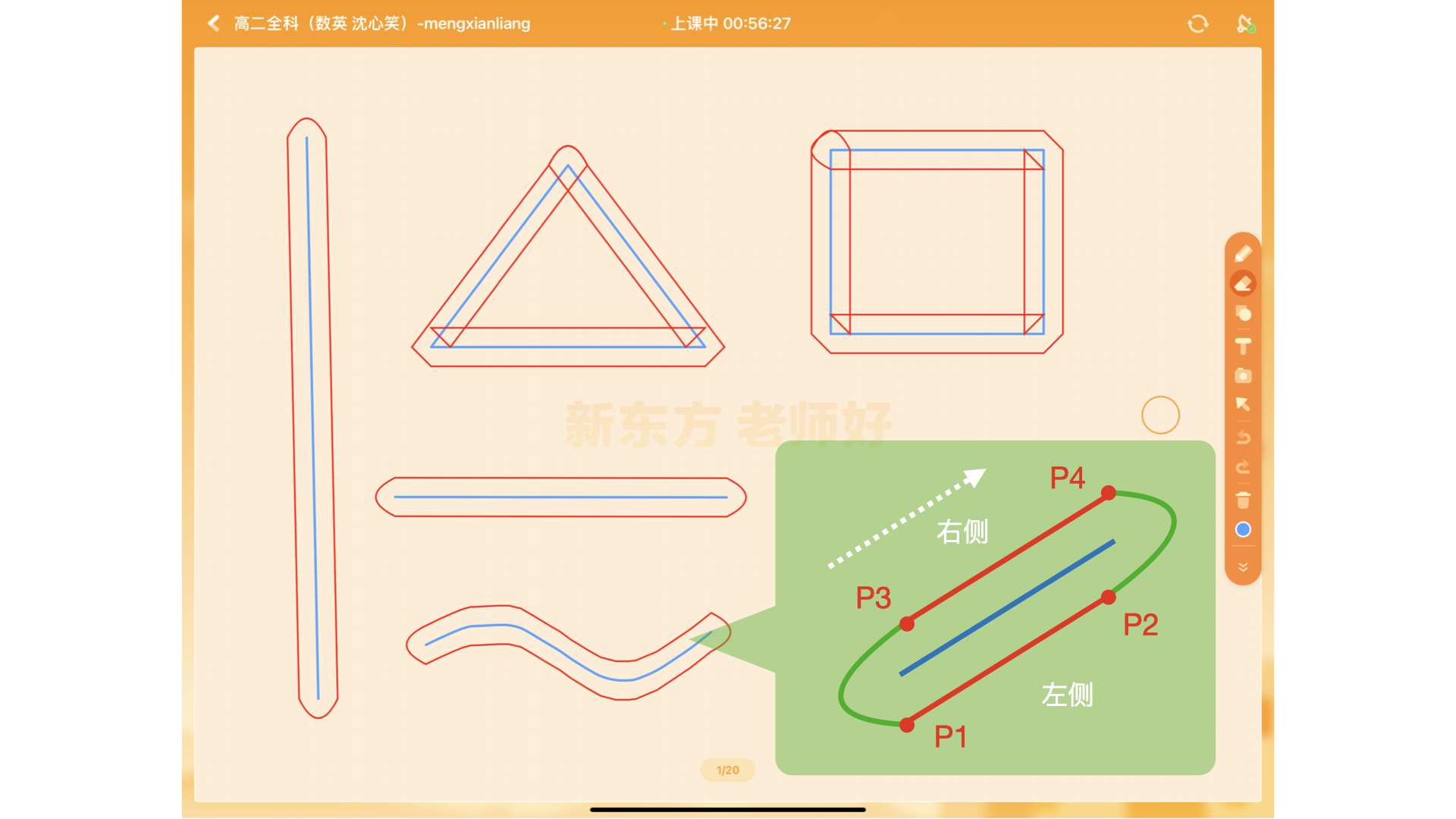
玩转贝塞尔曲线 - 图16

3、贝塞尔曲线应用举例

3.1 作为视图的运动路径

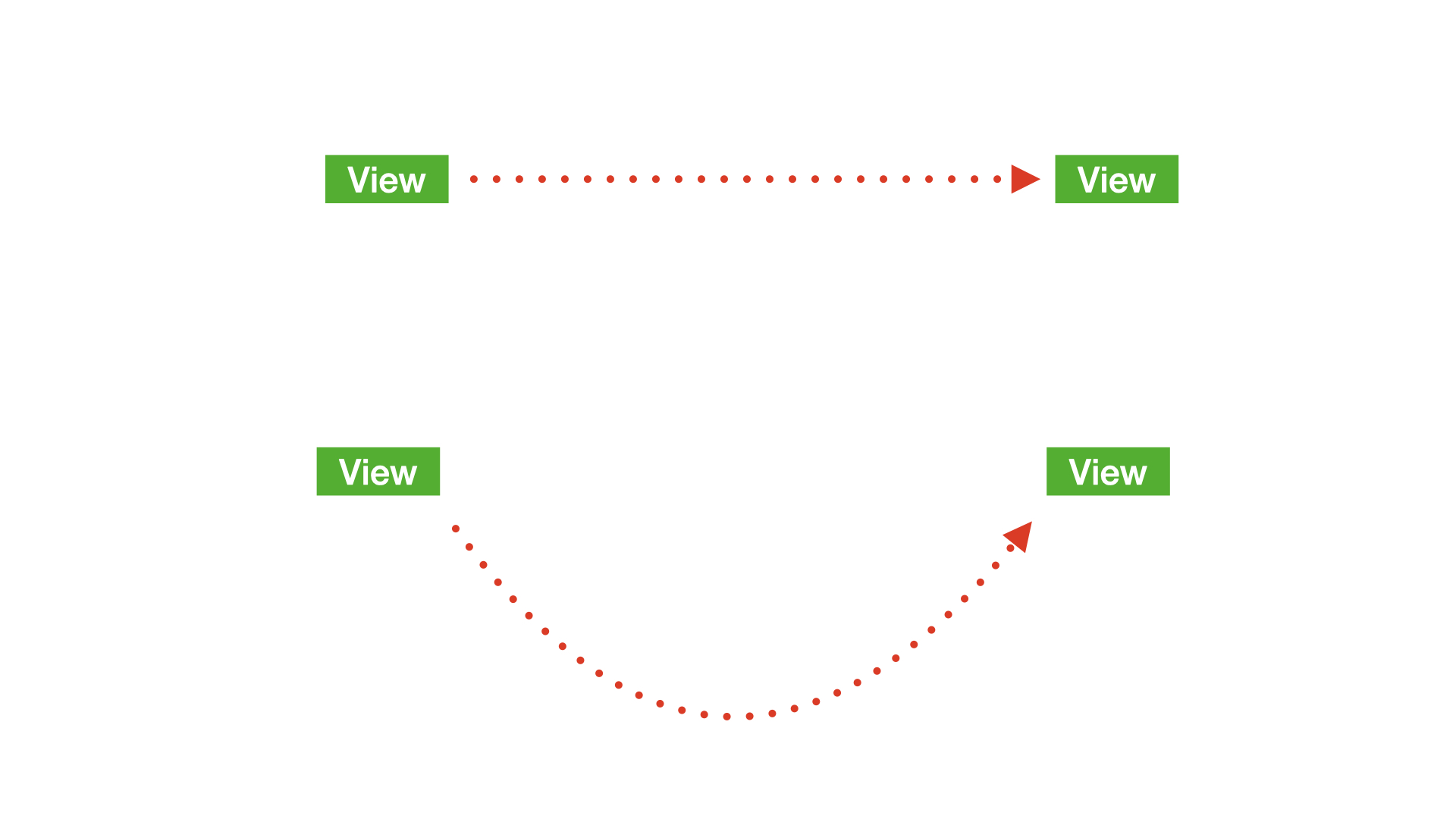
正常的View(视图)对象移动可以通过调整frame实现，如果需要查看移动轨迹，可以使用基本动画将view的移动轨迹渲染出来。

  1. [UIView animateWithDuration:0.3 animations:^{
  2.     view.frame = frame;
  3. }];

如果移动路径是一条曲线，或者是比较复杂的路径，则需要用贝塞尔曲线绘制出运动的路径，在结合关键帧动画实现:

  1. UIBezierPath *path = [UIBezierPath bezierPath];
  2. CAKeyframeAnimation *animation = [CAKeyframeAnimation animationWithKeyPath:@"position"];
  3. animation.path = path;
  4. [view.layer addAnimation:animation forKey:@"YourKey"];

玩转贝塞尔曲线 - 图17
举例，圆球移动效果：
玩转贝塞尔曲线 - 图18
分析：

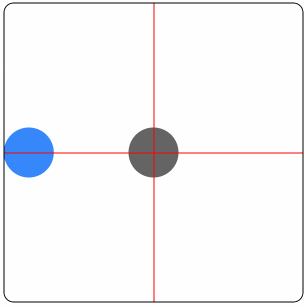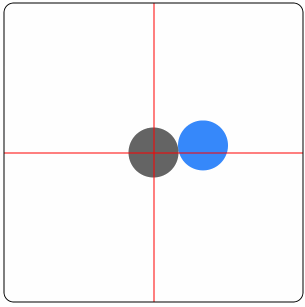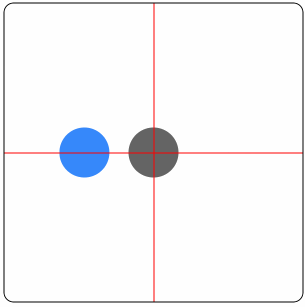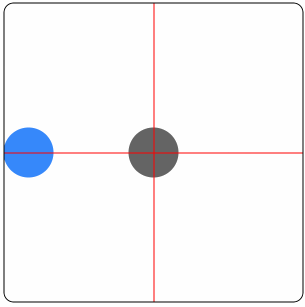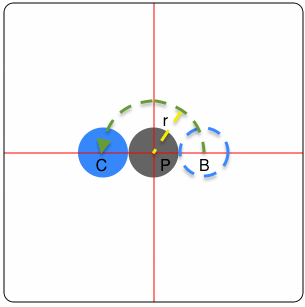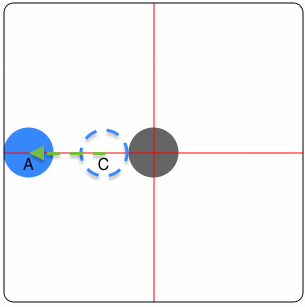玩转贝塞尔曲线 - 图19 玩转贝塞尔曲线 - 图20 玩转贝塞尔曲线 - 图21 玩转贝塞尔曲线 - 图22 
  1. UIBezierPath *path = [UIBezierPath bezierPath];
  2. path拼接一段从-π到0的逆时针半圆
  3. path拼接一段从π到0的逆时针半圆
  4. path拼接一段从右向左的直线
  5. CAKeyframeAnimation *animation = [CAKeyframeAnimation animationWithKeyPath:@"position"];
  6. animation.path = path;
  7. [view.layer addAnimation:animation forKey:@"YourKey"];

3.2 绘制函数曲线

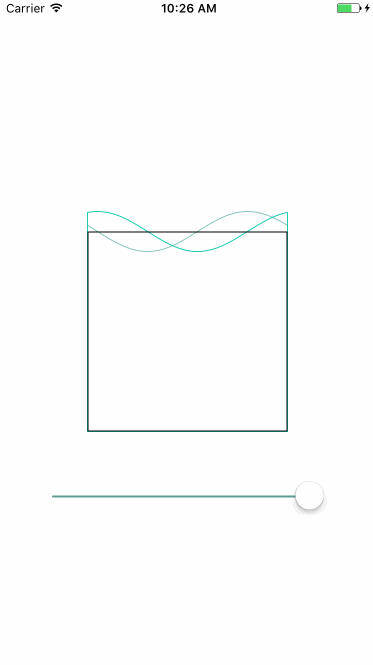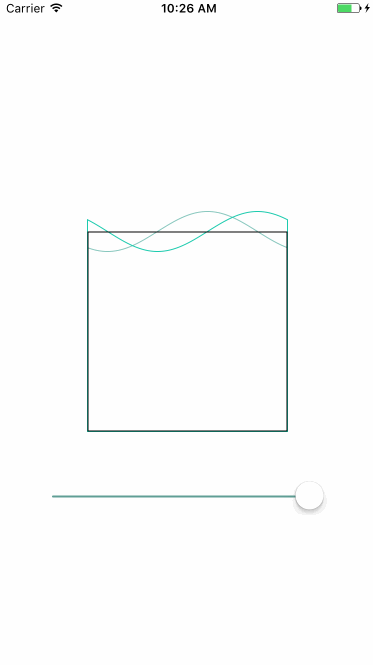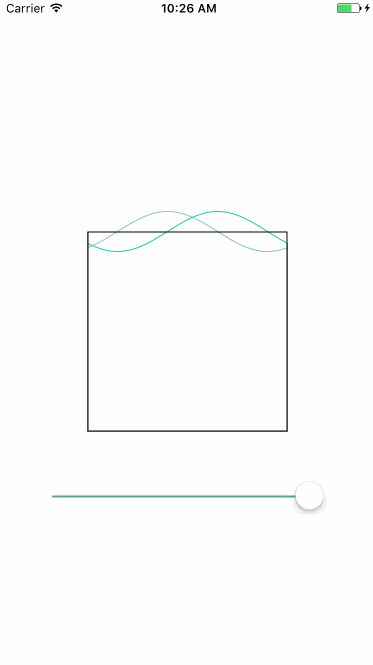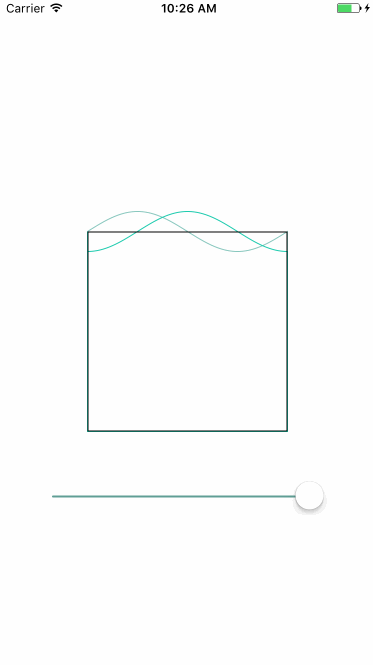
贝塞尔曲线是根据点进行绘制的，如果每个点的y都是x通过函数f进行计算所得：(x,f(x))，就可以绘制出函数f的曲线，以绘制波浪为例：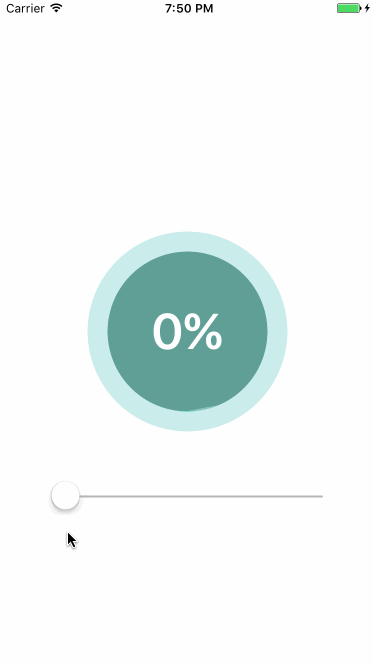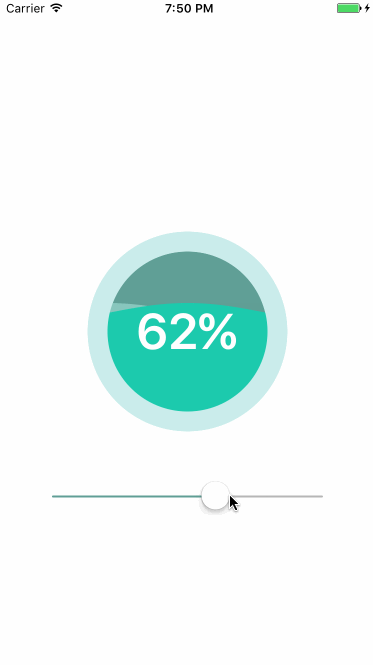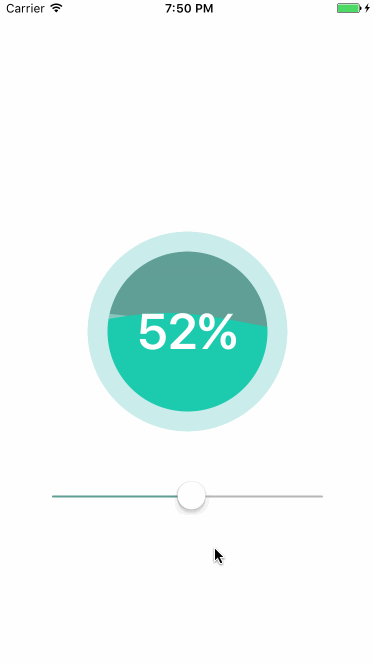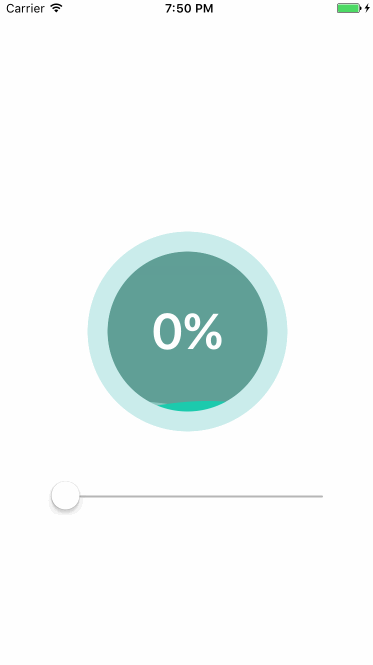
玩转贝塞尔曲线 - 图23
正弦曲线公式：y=Asin(ωx+φ)+k
A :振幅,曲线最高位和最低位的距离
ω :角速度,用于控制周期大小，单位x中起伏的个数
K :偏距,曲线上下偏移量
φ :初相,曲线左右偏移量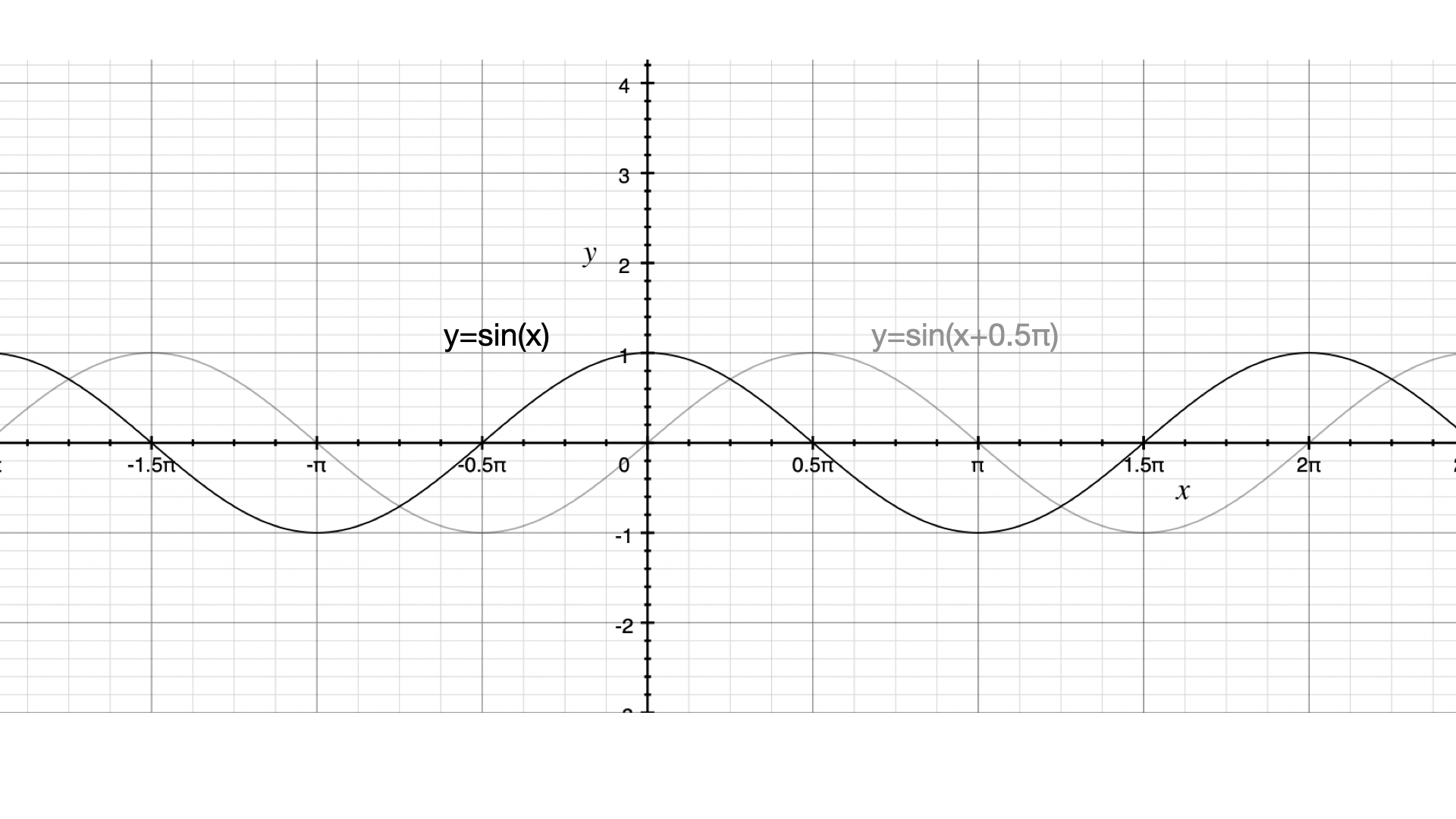
玩转贝塞尔曲线 - 图24
实现步骤如下：

绘制两条正弦函数曲线 更新函数初相 填充颜色
玩转贝塞尔曲线 - 图25 玩转贝塞尔曲线 - 图26 玩转贝塞尔曲线 - 图27

3.2 处理视图遮罩

系统给CALayer提供了mask属性

  1. @property(nullable, strong) __kindof CALayer *mask;

图层设置遮罩后，将以遮罩区域显示，如下图所示，给视图添加一个圆形遮罩，除圆形遮罩区域后，其它部分将不再显示：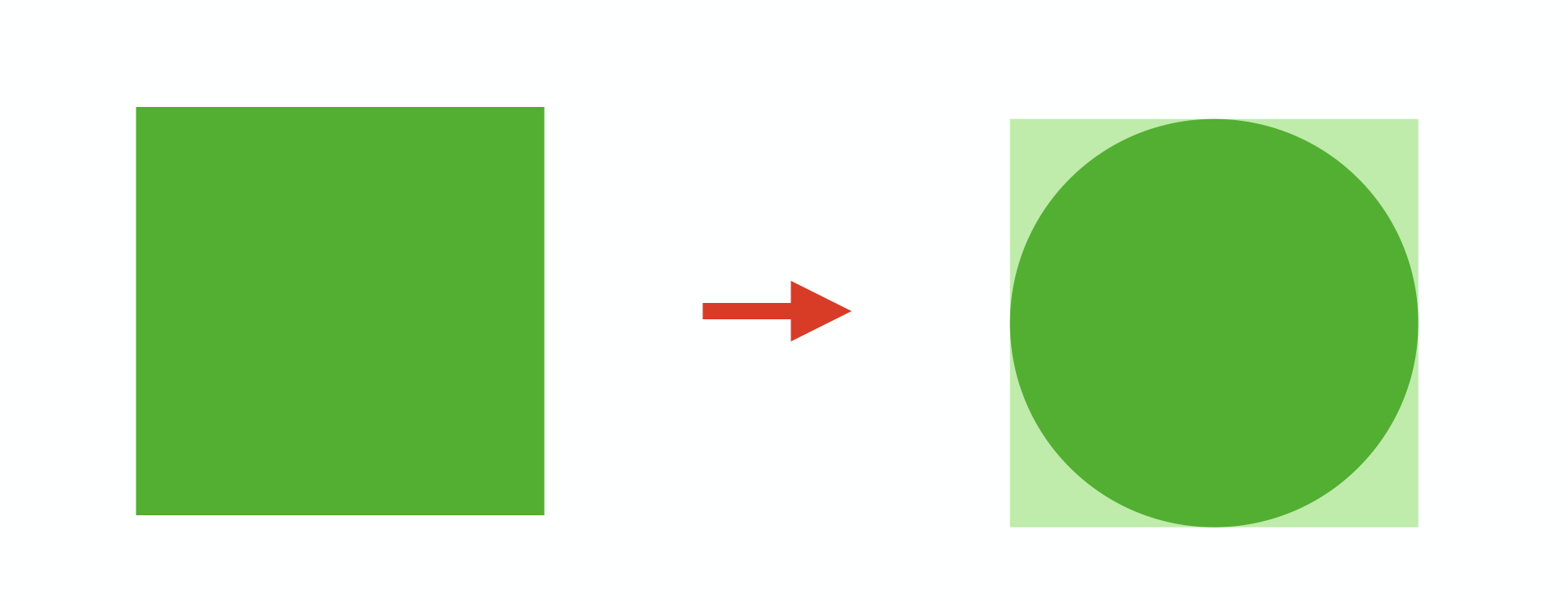
玩转贝塞尔曲线 - 图28
举例1，百度贴吧加载效果：
玩转贝塞尔曲线 - 图29
分析：共由三层组合而成，包括底层蓝色文字，中间白色文字+灰色波浪层，顶部白色文字+蓝色波浪层，其中波浪并没有直接绘制出来，而是作为了图层的mask，使白色文字以波浪的形式动态展示。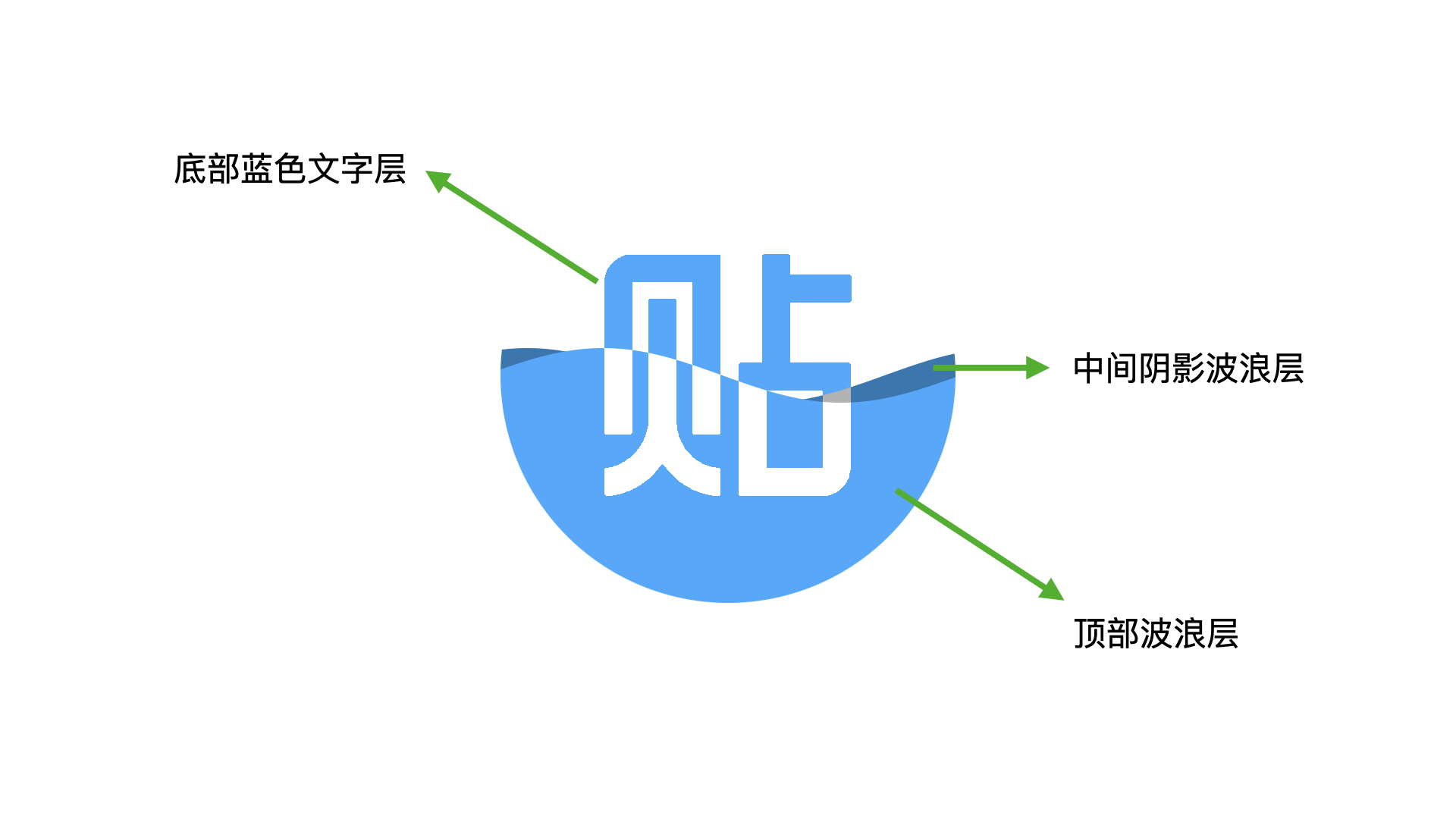
玩转贝塞尔曲线 - 图30
举例2，视图间专场效果：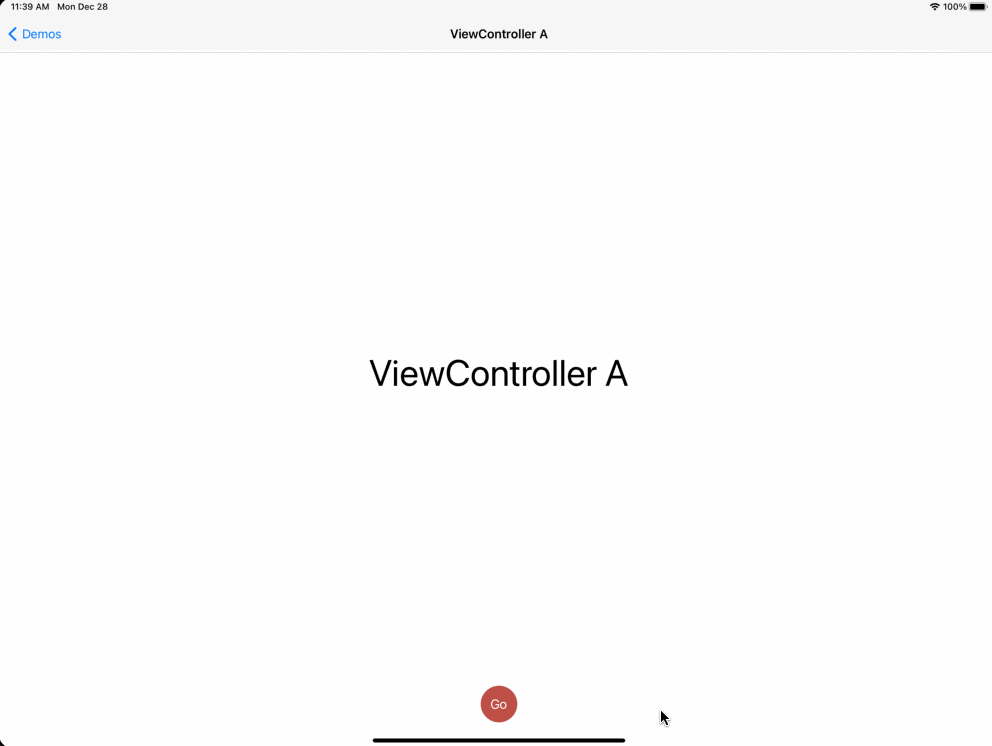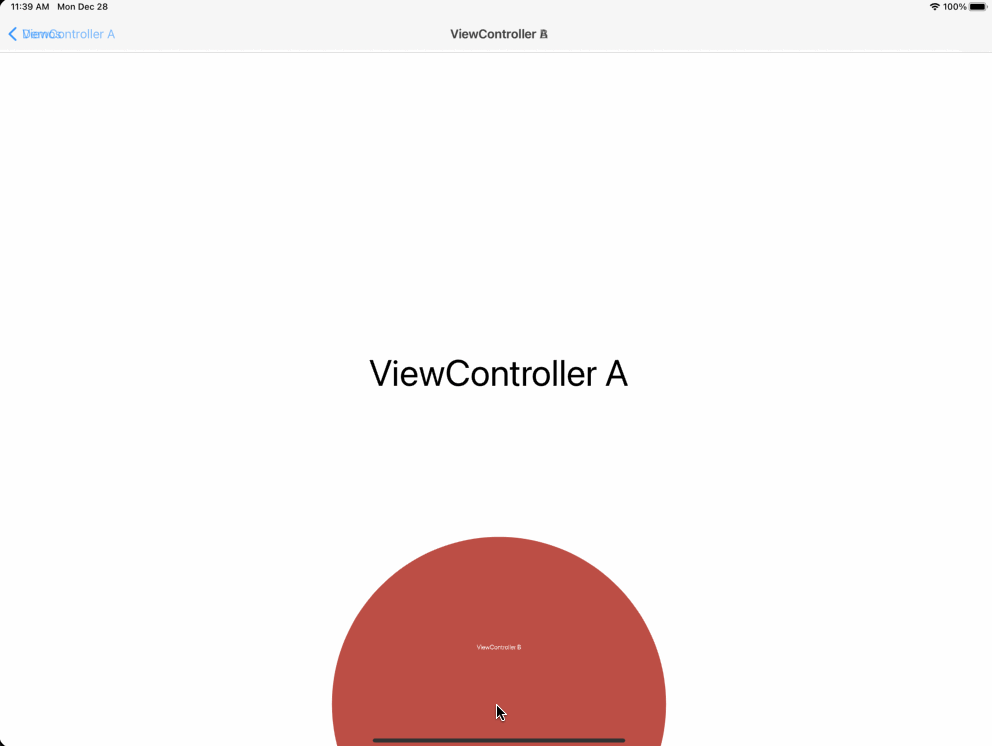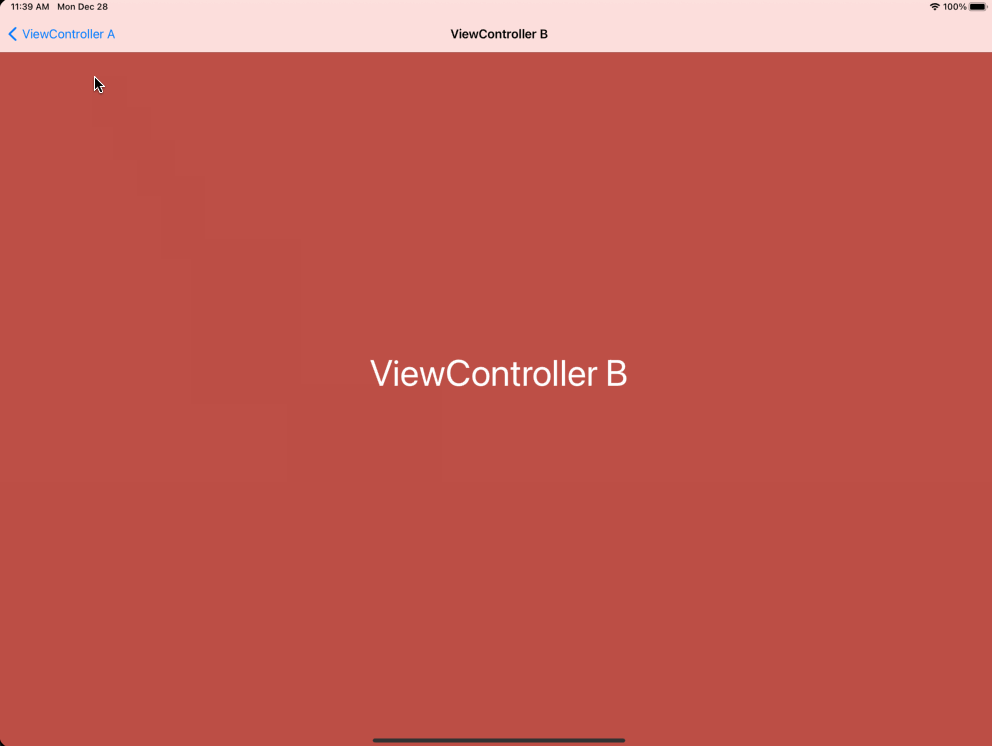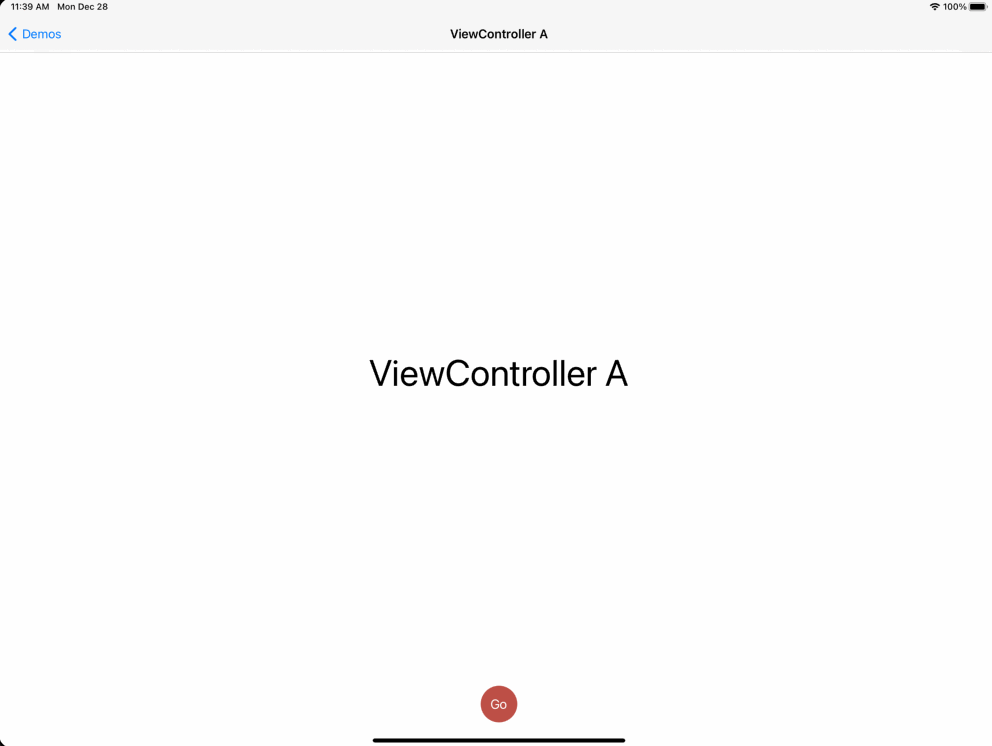
玩转贝塞尔曲线 - 图31
分析：
以按钮点击位置为圆心，半径从0到R，动态绘制圆形区域，以圆形区域作为试图的遮罩，再结合缩放效果，就可以实现上图的转场效果。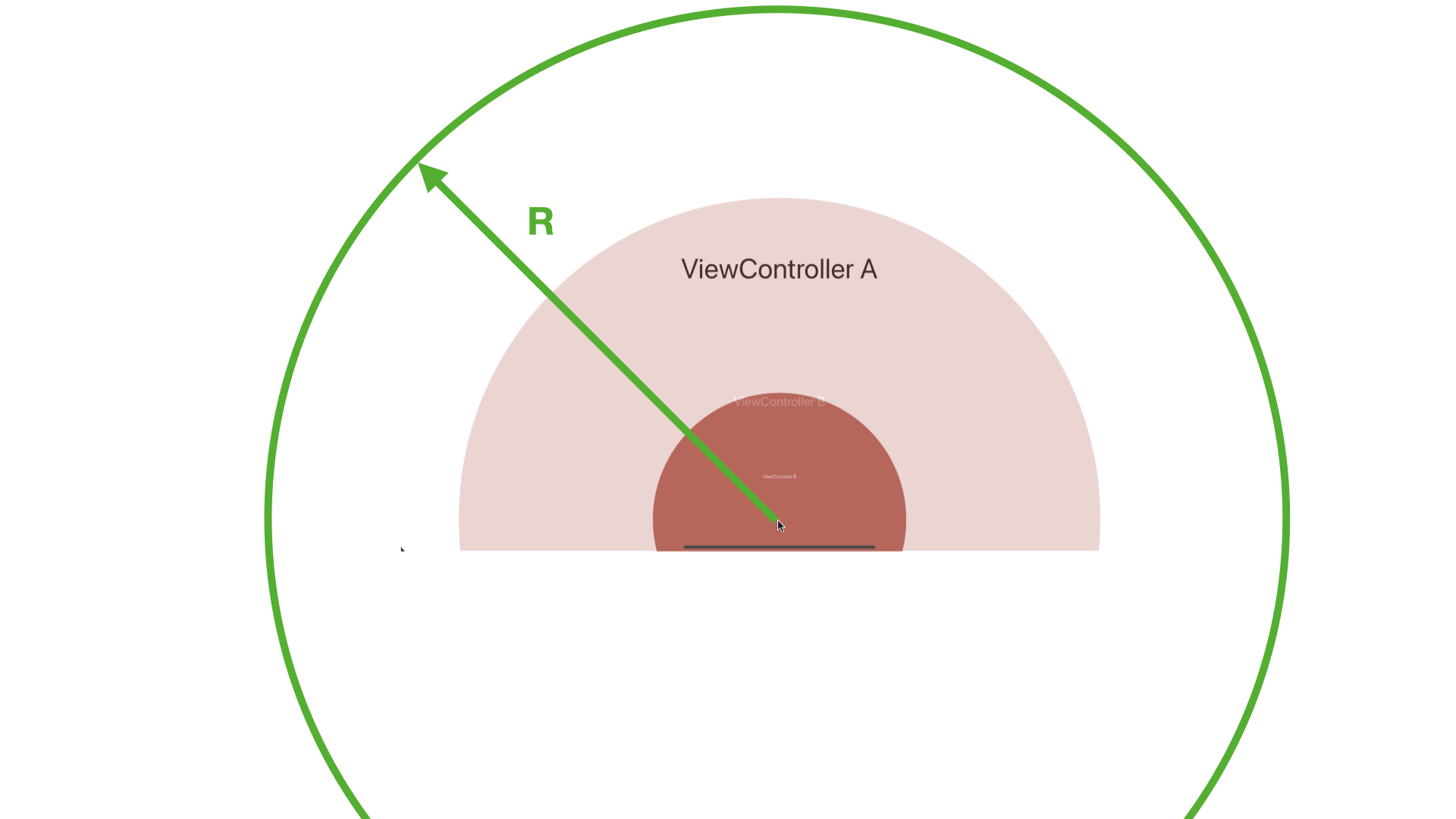
玩转贝塞尔曲线 - 图32

3.3 贝塞尔曲线交互

玩转贝塞尔曲线 - 图33
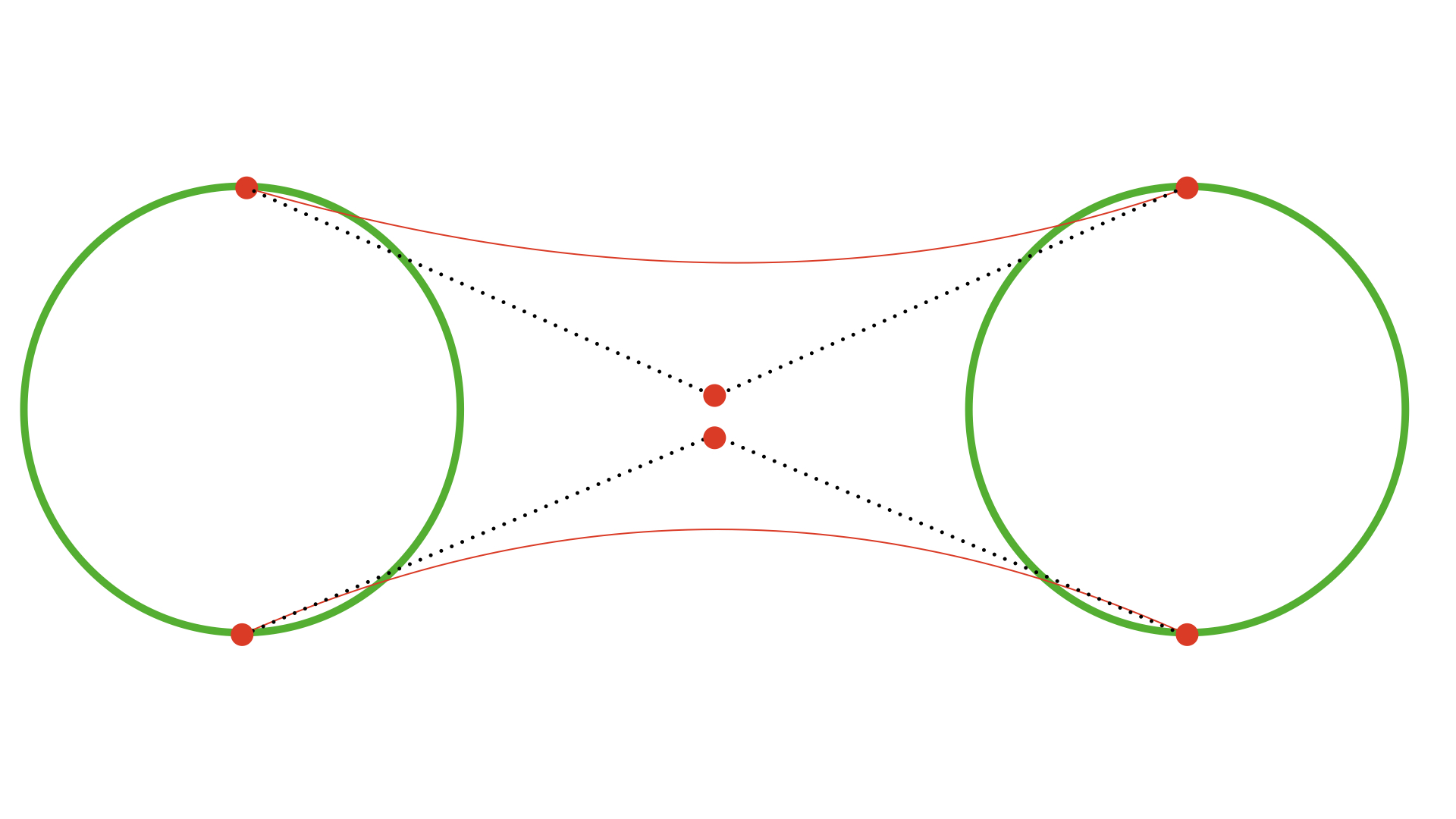
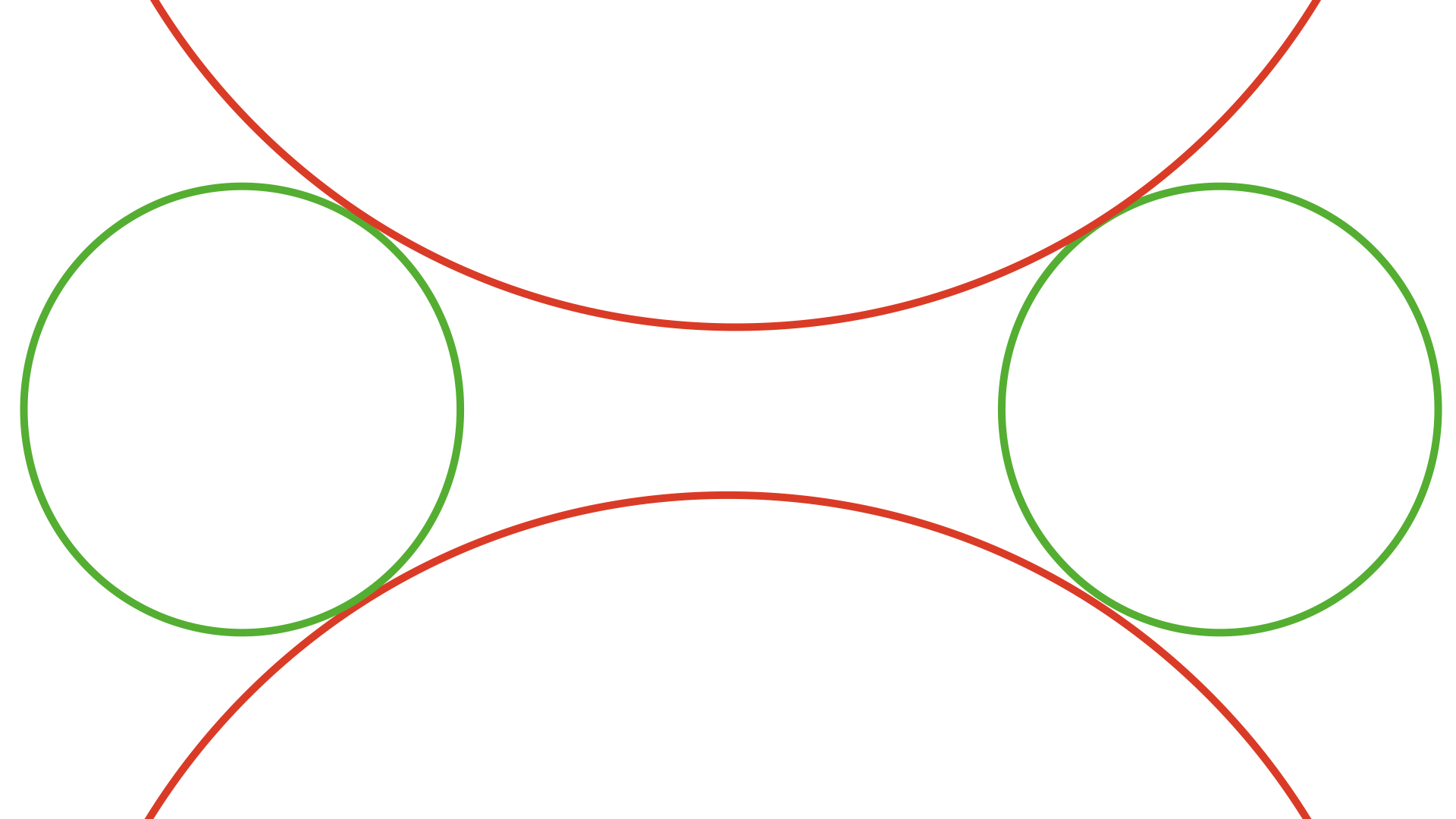
要实现QQ未读消息这样的黏性拖拽效果，主要实现部分是连接固定点和拖动点的曲线部分，由之前总结的经验可得一下几种方案：

绘制两条贝塞尔曲线 绘制两个外接圆 绘制两条函数曲线 其它方案
玩转贝塞尔曲线 - 图34 玩转贝塞尔曲线 - 图35 玩转贝塞尔曲线 - 图36 …

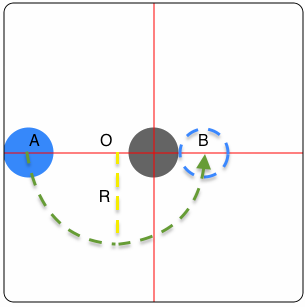
以第一种为例：需要在拖动的过程中，确定两个控制点的位置，并且使两个控制点间距越来越小，形成黏性效果，加入辅助线效果如下：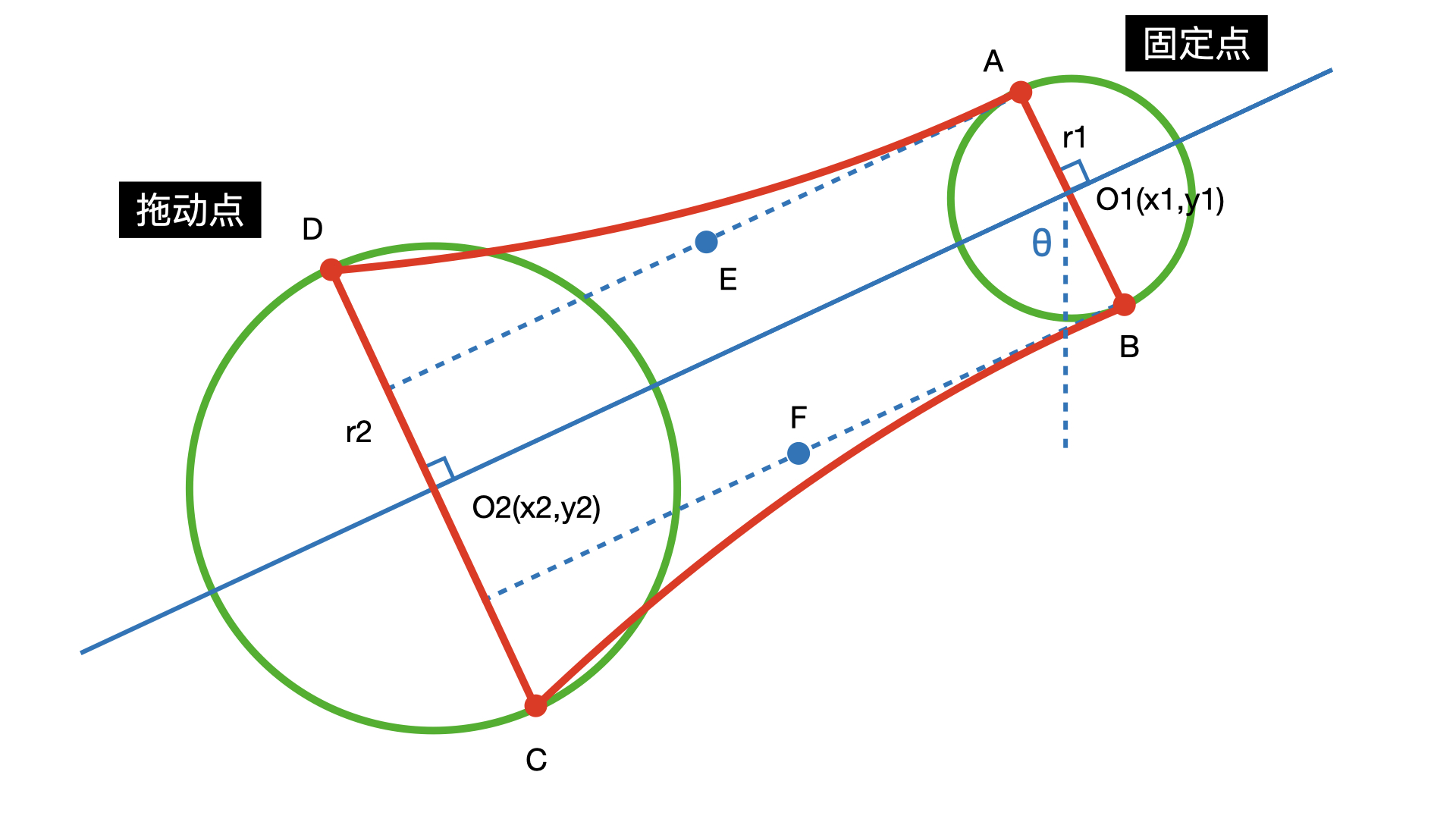
玩转贝塞尔曲线 - 图37
将UI问题转化为数学问题，理解起来就会比较方便：
已知条件为点O1和O2的坐标，可计算出O1和O2的间距和直线O1O2和竖直方向的夹角θ
根据角θ和AB和CD与O1O2的垂直关系，可计算出点A、B、C、D的坐标
最后计算出点E和点F
利用贝塞尔曲线在点A和点D、点B和点C之间绘制平滑曲线，在点A和点B、点C和点D间绘制直线，拼接成一个闭合的区域：

  1. //计算出两点间距离
  2. CGFloat d = sqrtf((x2-x1)*(x2-x1) + (y2-y1)*(y2-y1));
  4. //计算出角θ的正弦和余弦值
  5. CGFloat sinθ = (x2 - x1)/d;
  6. CGFloat cosθ = (y2 - y1)/d;
  8. //根据sinθ、cosθ、两点坐标，计算出A、B、C、D的坐标
  9. CGPoint pointA = CGPointMake(x1 - r1*cosθ, y1 + r1*sinθ);
  10. CGPoint pointB = CGPointMake(x1 + r1*cosθ, y1 - r1*sinθ);
  11. CGPoint pointC = CGPointMake(x2 - r2*cosθ, y2 + r2*sinθ);
  12. CGPoint pointD = CGPointMake(x2 + r2*cosθ, y2 - r2*sinθ);
  14. //计算出点A点B计算出点O、P的坐标
  15. CGPoint pointE = CGPointMake(pointA.x + (d/2)*sinθ, pointA.y + (d/2)*cosθ);
  16. CGPoint pointF = CGPointMake(pointB.x + (d/2)*sinθ, pointB.y + (d/2)*cosθ);
  18. //绘制曲线
  19. UIBezierPath *path = [UIBezierPath bezierPath];
  20. [path moveToPoint:pointA];
  21. [path addLineToPoint:pointB];
  22. [path addQuadCurveToPoint:pointD controlPoint:pointF];
  23. [path addLineToPoint:pointC];
  24. [path addQuadCurveToPoint:pointA controlPoint:pointE];
  25. [path closePath];
  27. //显示曲线
  28. self.shadowLayer.path = path.CGPath;

4、总结

贝塞尔曲线除了绘制还可以做一些辅助性的工作，在遇这类问题时，可以先转化为数学问题，解决起来就会相对简单一点。

Demo

https://github.com/mengxianliang/BezierPathDemo