动规｜115. 不同的子序列

题目

描述

• 给定一个字符串 s 和一个字符串 t ，计算在 s 的子序列中 t 出现的个数。
• 字符串的一个 子序列 是指，通过删除一些（也可以不删除）字符且不干扰剩余字符相对位置所组成的新字符串。（例如，”ACE” 是 “ABCDE” 的一个子序列，而 “AEC” 不是）

• 题目数据保证答案符合 32 位带符号整数范围。

  示例

  示例1：

• 输入：s = “rabbbit”, t = “rabbit”

• 输出：3
• 解释：

如下图所示, 有 3 种可以从 s 中得到 “rabbit” 的方案。
(上箭头符号 ^ 表示选取的字母)
rabbbit
^^^^ ^^
rabbbit
^^ ^^^^
rabbbit
^^^ ^^^

示例2：

• 输入：s = “babgbag”, t = “bag”
• 输出：5
• 解释：

如下图所示, 有 5 种可以从 s 中得到 “bag” 的方案。
(上箭头符号 ^ 表示选取的字母)
babgbag
^^ ^
babgbag
^^ ^
babgbag
^ ^^
babgbag
^ ^^
babgbag
^^^

提示

• 0 <= s.length, t.length <= 1000

• s 和 t 由英文字母组成

  信息

• 2021 年 03 月 20 日

• 链接：https://leetcode-cn.com/problems/distinct-subsequences/

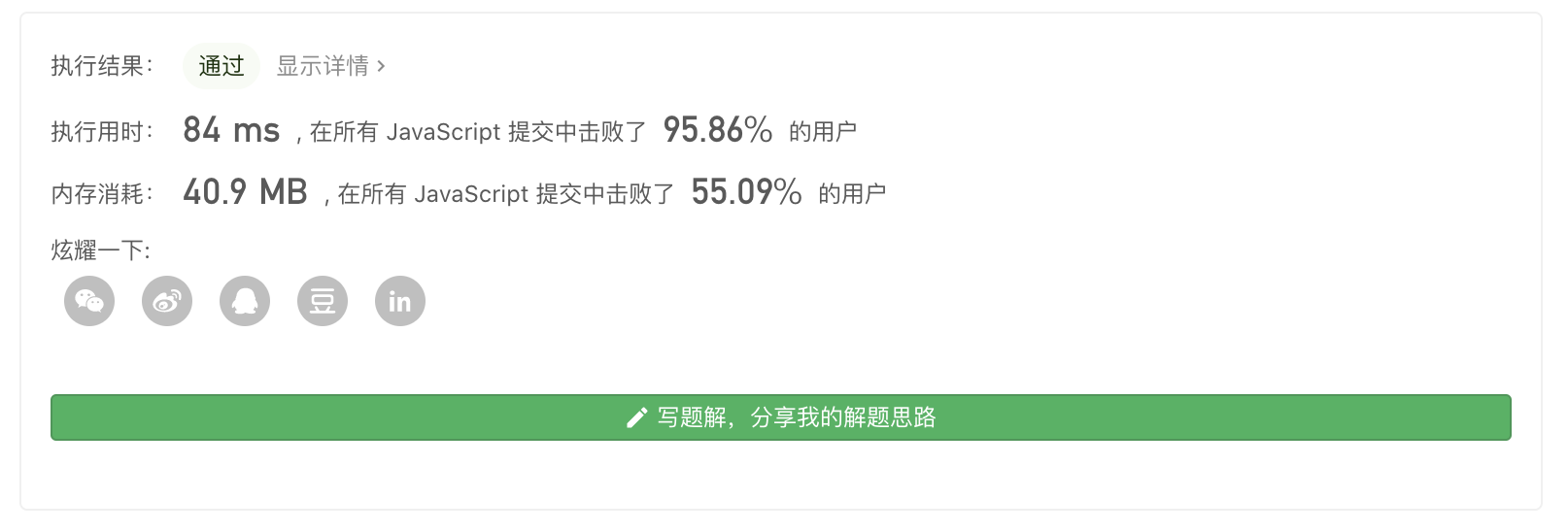
  提交记录

  

  解答

  思路

• 使用动态规划的思路进行迭代

• 首先将 t 拆分成多个单字符，按单字符去寻找 s 中当前字符出现的位置
• 下面内容，使用例子 s 为 babbg，t 为 ab 举例
• 从 t 中取字符 a，查询 a 在 s 中出现的次数
• 只需要创建数组 ta 长度为 s.length，默认值为 0， ta = [0, 0, 0, 0, 0]
• 遍历 s，更新数组 ta
  • 如果 s[i] !== a ，s[i] = s[i - 1]
  • 如果 s[i] === a , s[i] = s[i - 1] + 1

• 通过以上操作可得 ta = [0, 1, 1, 1, 1]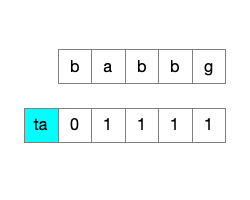

  

• 所以可直接从 ta 数组中知道字符串 s 中 a 字符的个数为 3 即 ta[s.length - 1]

• 按以上思路，将 t 拆分成 a、b 两个单独的字符，去字符串 s 中查找它们出现的次数，可以得下图所示结果

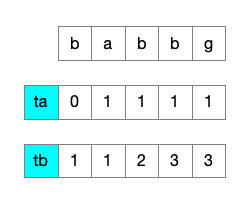
• 然后将 a、b 组合成字符串作为子序列 ab，去字符串 s 中查找出现此子序列的次数
  • 对 ab 进行遍历
  • 先用 a 去查，此时与 ta 的效果类似
  • 再用 b 去查，因为要考虑 a 是否有效，所以需要将 a 的查询结果作为依据，当查到 b 时，需要检测此字符前出现 a 的个数，以及前面已经查过的符合条件的 b 的个数，这两个加起来的和就是当前符合条件的 b 的个数
  • 如下图所示

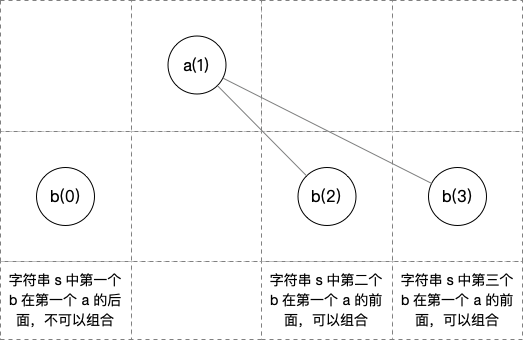
• 可得结果

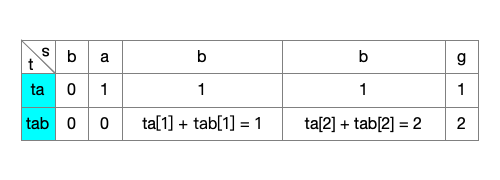
• tab = [0, 0, 1, 2, 2]
  • 然后 tab 数组的最后一个元素即为想要的答案，s 中 子元素 t 的个数为 2
  • 根据上面的推演过程，可以逐步抽离动态规划的公式
• 声明 dp[i][j]，i 的范围是 0 -> t.lenth，j 的范围是 0 -> s.length
• 结合上面的例子 s = babbg t = ab
• dp[0] = ta 用于记录遍历字符串 babbg 的过程中子字符串 a 在每个位置前出现的次数
  • dp[0][0] = 0 代表在字符串 babbg 中前 1 个字符中拥有 0 个子字符串 a
  • dp[0][1] = 1 代表在字符串 babbg 中前 2 个字符中拥有 1 个子字符串 a
  • dp[0][2] = 1 代表在字符串 babbg 中前 3 个字符中拥有 1 个子字符串 a
• dp[1] = tab 用于记录遍历字符串 babbg 的过程中子字符串 ab 在每个位置前出现的次数
  • dp[1][2] = 1 代表在字符串 babbg 中前 3 个字符中拥有 1 个子字符串 ab
  • dp[1][4] = 2 代表在字符串 babbg 中前 5 个字符中拥有 2 个子字符串 ab
    • 所以可得动态规划的转移方程为

• 由于要考虑空字符串 t = '' 和 s = '' 的情况，可以从后向前遍历，然后将空字符串的情况补充在尾部
• 用 dp[i][s.length] 代表 s = '' 的情况，此种情况只有当 t = '' 时才为 1，否则全为 0
• 用 dp[t.length][j] 代表 t = '' 的情况，此种情况全为 1
• 此时公式就调整为

代码

/**
 * @param {string} s
 * @param {string} t
 * @return {number}
 */
var numDistinct = function(s, t) {
    const sLength = s.length
    const tLength = t.length
    const sLength1 = sLength + 1
    const dp = []
    // 过滤特殊值
    if(tLength === 0){
        return 1
    }
    if(sLength === 0 || sLength < tLength){
        return 0
    }
    // 初始化 dp
    for(let i = 0; i < tLength; i ++){
        dp[i] = new Array(sLength1).fill(0)
    }
    dp[tLength] = new Array(sLength1).fill(1)
    // 外循环，代表 t 的迭代
    for(let i = tLength - 1; i >= 0; i --){
        // 内循环，代表 s 的迭代
        for(let j = sLength - 1; j >= 0; j --){
            dp[i][j] = dp[i][j + 1]
            if(t[i] === s[j]){
                dp[i][j] += dp[i + 1][j + 1] 
            }
        }
                // 如果没找到子字符串，则过滤后序的操作
        if(dp[i][0] === 0){
            return 0
        }
    }
    return dp[0][0]
};