第2章

程序2-1

diffMat=tile(inX, (dataSetSize,1))-dataSet

《机器学习实战》笔记之Chapter2-KNN - 图1

tile就是平铺，瓦片，操作系统桌面的背景图片里有这词

argsort返回的是位置[DoubleLongLeftRightArrow]Ordering

  1. orders = Ordering[list = {1, 3, 5, 2, 8, 4}]

{1,4,2,6,3,5}

  1. Extract[list, List /@ orders]

{1,2,3,4,5,8}

矩阵里按距离计算，对距离排序后然后从Labels里提取做循环，其实就是intX跟矩阵里的每个Vector进行一次距离的度量，然后再选择距离最小的点。

  1. classify0[vec_, dataSet_, labels_, k_] := Block[{},dataSetSize = dataSet // Dimensions;
  2. diffMat = ConstantArray[vec, dataSetSize[[1]]] - dataSet;
  3. (*注意这里dataSetSize索引取值和vec是一维还是二维的变化情况*)sqDiffMat = diffMat^2;
  4. sqDistances = sqDiffMat // Total[#, {2}] &;
  5. (*这里Total类比numpy里的一些axis的操作，也可以用Total/@#&*)distances = Sqrt[sqDistances];
  6. sortedDistIndices = distances // Ordering;
  7. classCount = Association[];
  8. For[i = 1, i <= k, i++,voteIlabel = labels[[sortedDistIndices[[i]]]];
  9. If[KeyExistsQ[classCount, voteIlabel], classCount[voteIlabel] += 1,classCount[voteIlabel] = 1];
  10. ];
  11. Sort[classCount] // Reverse]
  13. vec = RandomReal[10, {2}];
  14. dataSet = RandomReal[10, {20, 2}];
  15. (*使用聚类算法标注一下。。。*)asso = Association[Flatten[Thread /@ Thread[FindClusters[dataSet, 4] -> CharacterRange["A", "D"]]]];
  16. labels = asso /@ dataSetdataSet // MatrixFormListPlot[{dataSet, {vec}}, PlotStyle -> PointSize[.05],  Epilog -> Thread[Text[labels, dataSet]]]

{A,B,B,C,B,D,C,D,B,B,C,C,B,C,C,B,D,D,A,A}

(6.92693 3.23962
2.91501 1.20566
3.3583 4.18153
9.31141 9.96102
4.4195 3.98825
2.10963 6.65032
6.92627 7.38901
4.00941 5.74839
3.24231 3.88988
3.66842 0.452613
6.00458 8.59236
7.30268 8.02751
4.3686 1.43087
7.78579 5.58951
8.74832 7.19463
4.13234 3.61192
4.1028 7.52184
2.95764 8.73533
9.85549 2.77611
8.92983 2.71117

)

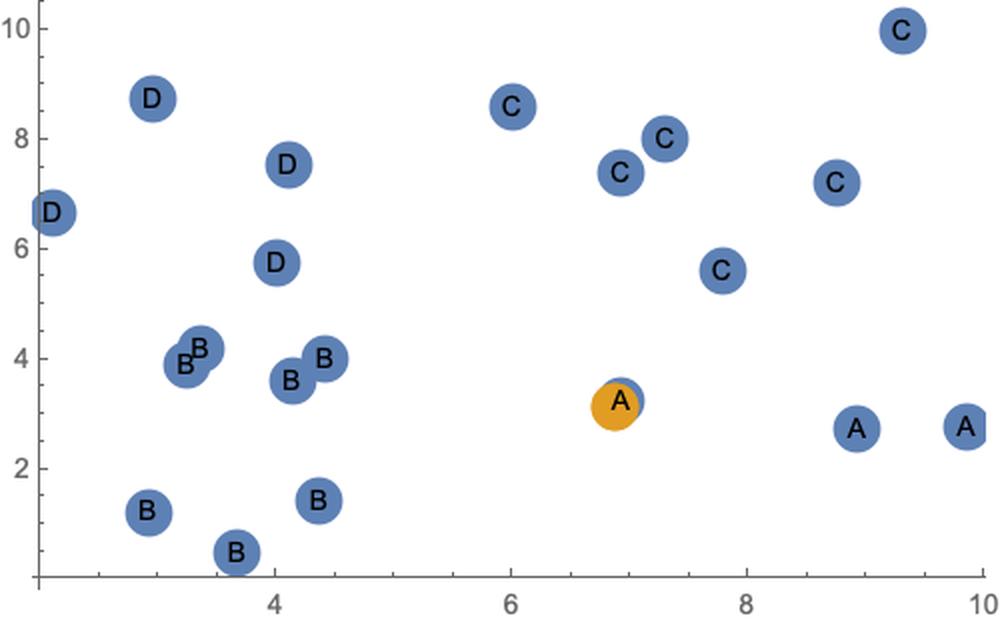
《机器学习实战》笔记之Chapter2-KNN - 图2

  1. classify0[vec, dataSet, labels, 10]

<|B->5,A->3,D->1,C->1|>

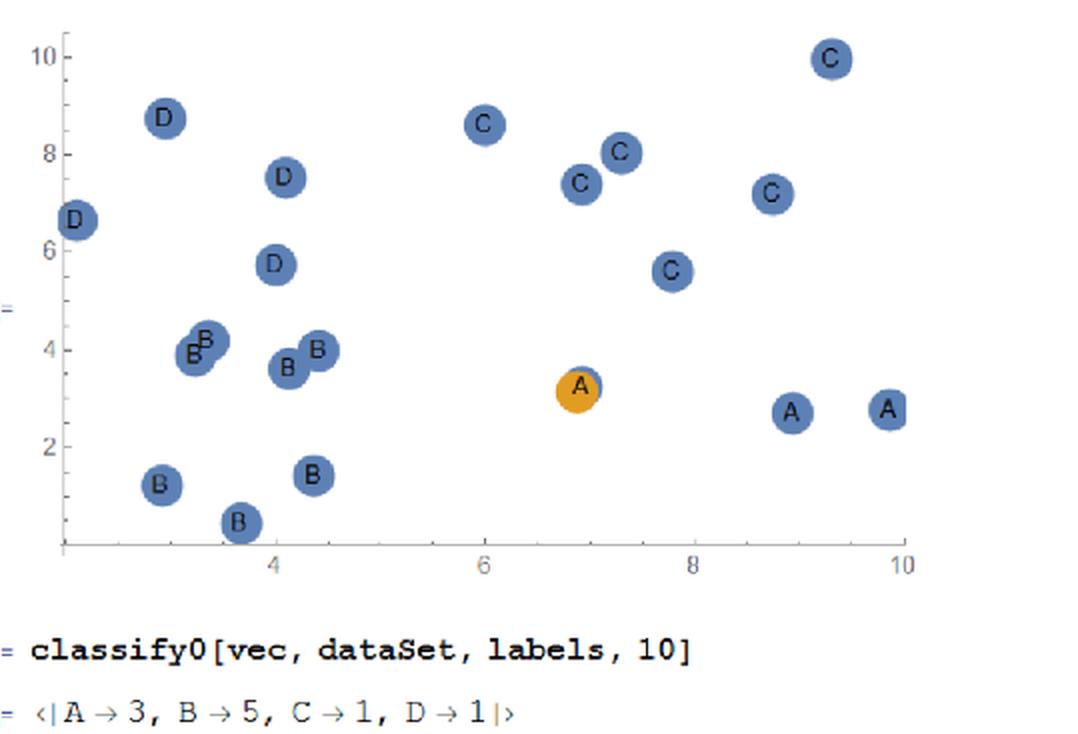
《机器学习实战》笔记之Chapter2-KNN - 图3

优化版

如果要在大量的数据上进行一些实战，加些简单的策略，比如聚类后，对每分组索引等，然后再对小类[区域]进行更细的比对，或使用KD-Tree等等，这些属于算法和数据结构的优化

Mathematica版代码优化

在类比numpy数组的操作中，还是自己从矩阵结构计算了一下欧氏距离，那么如果调用一个计算+map一下呢？

  1. classify1[vec_, dataSet_, labels_, k_] := Block[{},distances1 = EuclideanDistance[vec, #] & /@ dataSet;
  2. sortedDistIndices = distances1 // Ordering;
  3. classCount = Association[];
  4. For[i = 1, i <= k, i++,voteIlabel = labels[[sortedDistIndices[[i]]]];
  5. If[KeyExistsQ[classCount, voteIlabel], classCount[voteIlabel] += 1,classCount[voteIlabel] = 1];
  6. ];
  7. Sort[classCount] // Reverse]
  9. classify1[vec, dataSet, labels, 10]

<|B->5,A->3,D->1,C->1|>

如果使用pandas的话，也可以对整个数据集进行一次apply一个函数，python[DoubleLongRightArrow]numpy[DoubleLongRightArrow]pandas，然后代码越来越短。。。

  1. classify2[vec_, dataSet_, labels_, k_] := Block[{},asso = AssociationThread[dataSet -> labels];
  2. assoSorted = KeySortBy[asso, EuclideanDistance[vec, #] &];
  3. res = Counts[Values@assoSorted[[1 ;; k]]] // Sort // Reverse]
  5. classify2[vec, dataSet, labels, 10]

<|B->5,A->3,D->1,C->1|>

当然也可以写成一句话[DoubleLongRightArrow]真尼玛短
这就是学习使用一些高级函数和数据结构，在做实验，学习一些东西时，可以先把一些不是重点的东西pass掉，关注如何调一些关键参数，做出效果等，当然前提是数据是理想的。

  1. Counts[KeySortBy[AssociationThread[dataSet -> labels], EuclideanDistance[vec, #] &][[1 ;; 10]] // Values] // Sort // Reverse

<|B->5,A->3,D->1,C->1|>

Summary

  1. << "/Users/hypergroups/Nutstore/Wolfram \Mathematica/DeployProjects/MyMarkDown/MyMarkDown.wl"
  3. Notebook2Markdown[EvaluationNotebook[],  "dirOutput" -> NotebookDirectory[], "title" -> "knn",  ImagePrefix -> "https://raw.githubusercontent.com/HyperGroups/\MathematicaMachineLearning/master/Articles/Notes@\MachineLearningInAction/Chapter2"]