时序分解总结

很多时序波形，在不同的时间粒度上规律和驱动因素不同，在异常检测和趋势预测等多数场景，希望能在部分尺度上发现体现的相关因素。比方说发现KPI指标的趋势项、周期项、残余项，根据残余项发现可能的异常或者故障。针对三者可分别建模，利用自回归拟合，得到合适的预测模型（多数会去除趋势项）。
常见的时序分解算法有STL、奇异谱分析（SSA）、经验模态分解（EMD）、小波变换、SuperSmooth、传统线性滤波等。这里重点介绍前4种算法。

STL分解

STL（Seasonal and Trend Decomposition Using LOESS）是1990年由密歇根大学的R. B. Cleveland教授及AT&T Bell实验室的W. S.Cleveland等学者提出的一种时序分解方法。将时间序列分解为趋势（Trend）、周期（Seasonal）、非规则（Irregular）3个成分。

该算法由内循环和外循环组成。内循环包含去趋势、周期子序列平滑、对平滑周期子序列的低通滤波处理等6个步骤；外循环的主要作用是引入一个稳健性权重项，以控制数据中异常值的影响，在下一阶段内循环的临近权重中会考虑该项。实际上，趋势分量和季节分量都在内循环中得到。循环结束后，季节项将出现一定程度的毛刺。因为在内循环中，平滑是在每一个截口中进行的，所以在按照时间顺序进行重排后，无法保证相邻时段的平滑。因此，还需要进行季节项的后平滑，后平滑基于局部二次拟合，且不需要在LOESS中进行稳健性迭代。
大致了解了STL的原理后，其实我们大多数情况是直接调用相关的库进行STL分析。

import statsmodels.api as sm
import matplotlib.pyplot as plt
import pandas as pd
from date_utils import get_gran, format_timestamp
dta = pd.read_csv('artificialWithAnomaly/art_daily_flatmiddle.csv',
                                   usecols=['timestamp', 'value'])
dta = format_timestamp(dta)
dta = dta.set_index('timestamp')
dta['value'] = dta['value'].apply(pd.to_numeric, errors='ignore')
dta.value.interpolate(inplace=True)
res = sm.tsa.seasonal_decompose(dta.value, freq=288)
res.plot()
plt.show()

注意这里使用的statsmodels里，提供了加法和乘法两种拆分模型，在实际使用中一般要明确具体方法。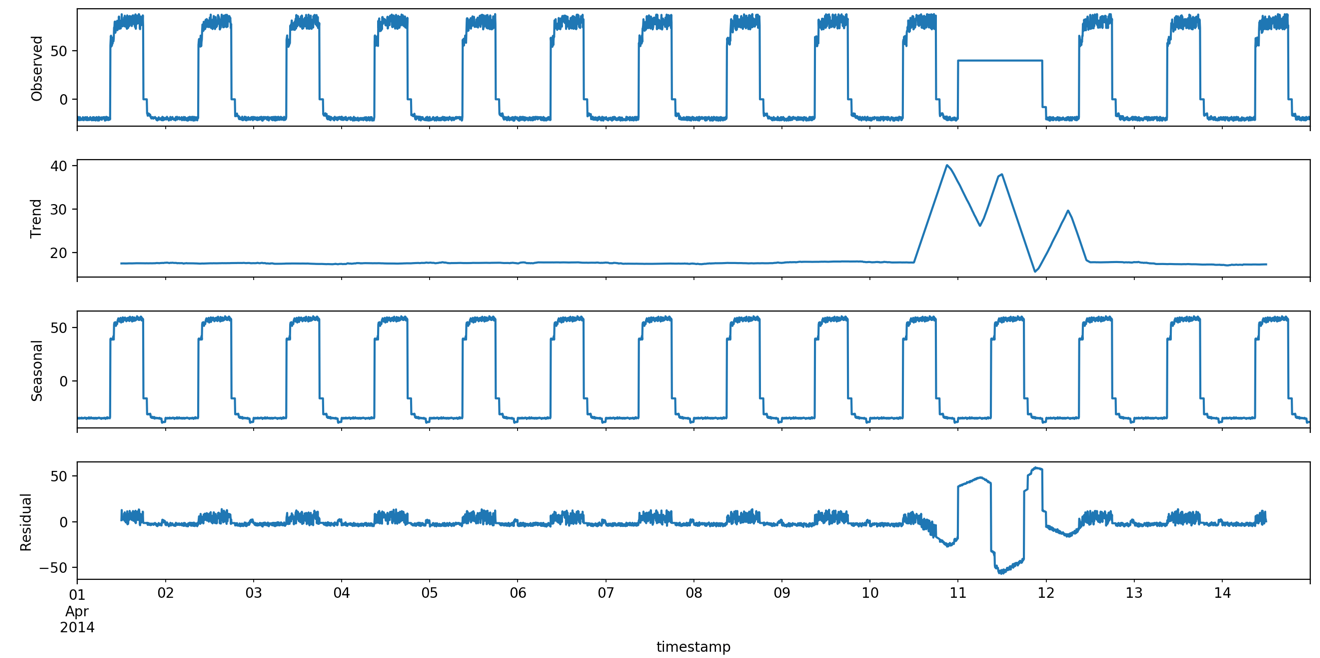

可参考https://www.cnblogs.com/en-heng/p/7390310.html里具体的算法说明

奇异谱分析（SSA）

在做变点分析的时候，会用到奇异谱进行转化。它根据观测到的时间序列构造轨迹矩阵，并对轨迹矩阵进行分解、重构，提取代表原时间序列不同成分的信号，如长期趋势信号、周期信号、噪声信号等，从而对时间序列的结构进行分析，并用于进一步预测。
奇异谱分析的基本思想是将观测到的一维时序数据Yt=(y1,y2,…,yT)转化为轨迹矩阵

式中，L为选取的窗口长度，K=T-L+1，计算并对其进行奇异值分解（SVD），得到其L个特征值及相应的特征向量，并将每个特征值所代表的信号进行分析组合，重构新的时间序列。奇异谱分析包括嵌入、SVD、分组、重构4个步骤。