RBM和DBN理论解读

深度学习的两类神经网络模型的原理，第一类是前向的神经网络，即DNN和CNN。第二类是有反馈的神经网络，即RNN和LSTM。今天我们就总结下深度学习里的第三类神经网络模型：玻尔兹曼机。主要关注于这类模型中的受限玻尔兹曼机（Restricted Boltzmann Machine，以下简称RBM）， RBM模型及其推广在工业界比如推荐系统中得到了广泛的应用。

1、限制波尔兹曼机（RBM）

玻尔兹曼机是一大类的神经网络模型，但是在实际应用中使用最多的则是RBM。RBM本身模型很简单，只是一个两层的神经网络，因此严格意义上不能算深度学习的范畴。不过深度玻尔兹曼机（Deep Boltzmann Machine，以下简称DBM）可以看做是RBM的推广。理解了RBM再去研究DBM就不难了，因此本文主要关注于RBM。
限制玻尔兹曼机 (Restricted Boltzmann machines, 简称RBM)是基于概率模型的无监督非线性特征学习器。当用 RBM 或 多层次结构的RBMs 提取的特征在馈入线性分类器（如线性支持向量机或感知机）时通常会获得良好的结果。

1.1 网络结构

RBM 的图形模型是一个全连接的二分图（fully-connected bipartite graph）。RBM是一种神经感知器，由一个显层和一个隐层构成，显层与隐层的神经元之间为双向全连接。如下图所示：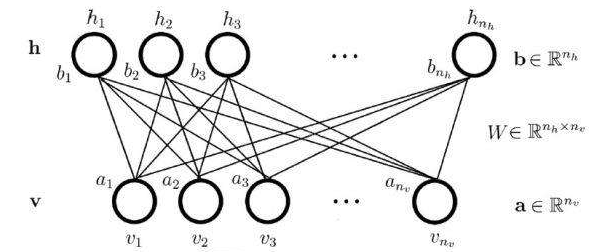

图1 RBM网络结构图
如图1所示，上面一层神经元组成隐藏层(hidden layer), 用向量表示隐藏层神经元的值。下面一层的神经元组成可见层(visible layer),用向量表示可见层神经元的值。隐藏层和可见层之间是全连接的，这点和DNN类似，但是隐藏层神经元之间是独立的，可见层神经元之间也是独立的。连接权重可以用矩阵表示。和DNN的区别是，RBM不区分前向和反向，可见层的状态可以作用于隐藏层，而隐藏层的状态也可以作用于可见层。隐藏层的偏置系数是向量，而可见层的偏置系数是向量。
常用的RBM一般是二值的，即不管是隐藏层还是可见层，它们的神经元的取值只为0或者1。本文只讨论二值RBM。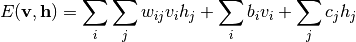

在上面的公式中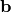， 和 分别是可见层和隐藏层的偏置向量。 模型的联合概率是根据能量来定义的: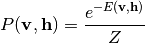

“限制”是指模型的二分图结构，它禁止隐藏单元之间或可见单元之间的直接交互。 这代表以下条件独立性成立: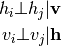

二分图结构允许使用高效的块吉比斯采样(block Gibbs sampling)进行推断。

1.2 RBM概率分布

RBM是基于基于能量的概率分布模型。怎么理解呢？分两部分理解，第一部分是能量函数，第二部分是基于能量函数的概率分布函数。
对于给定的状态向量和，则RBM当前的能量函数可以表示为：

有了能量函数，则我们可以定义RBM的状态为给定，的概率分布为：

其中为归一化因子，类似于softmax中的归一化因子，表达式为：

有了概率分布，我们现在来看条件分布：

其中为新的归一化系数，表达式为：

同样的方式，我们也可以求出。
有了条件概率分布，现在我们来看看RBM的激活函数，提到神经网络，我们都绕不开激活函数，但是上面我们并没有提到。由于使用的是能量概率模型，RBM的基于条件分布的激活函数是很容易推导出来的。我们以为例推导如下。

从上面可以看出， RBM里从可见层到隐藏层用的其实就是sigmoid激活函数。同样的方法，我们也可以得到隐藏层到可见层用的也是sigmoid激活函数。即：　

有了激活函数，我们就可以从可见层和参数推导出隐藏层的神经元的取值概率了。对于0,1取值的情况，则大于0.5即取值为1。从隐藏层和参数推导出可见的神经元的取值方法也是一样的。

1.3 RBM模型的损失函数与优化

RBM模型的关键就是求出我们模型中的参数、、。如果求出呢？对于训练集的m个样本，RBM一般采用对数损失函数，即期望最小化下式：

对于优化过程，我们是首先想到的当然是梯度下降法来迭代求出、、。我们首先来看单个样本的梯度计算, 单个样本的损失函数为：，我们先看看具体的内容：

注意，这里面表示的是某个特定训练样本，而指的是任意一个样本。
我们以的梯度计算为例：

其中用到了:

同样的方法，可以得到、的梯度。这里就不推导了，直接给出结果：


虽然梯度下降法可以从理论上解决RBM的优化，但是在实际应用中，由于概率分布的计算量大，因为概率分布有种情况, 所以往往不直接按上面的梯度公式去求所有样本的梯度和，而是用基于MCMC的方法来模拟计算求解每个样本的梯度损失再求梯度和，常用的方法是基于Gibbs采样的对比散度方法来求解，对于对比散度方法，由于需要MCMC的知识，这里就不展开了。对对比散度方法感兴趣的可以看参考文献中2的《A Practical Guide to Training Restricted Boltzmann Machines》，对于MCMC，后面我专门开篇来讲。

A Practical Guide to Training Restricted Boltzmann Machines.pdf

1.4 RBM在实际中应用方法

大家也许会疑惑，这么一个模型在实际中如何能够应用呢？比如在推荐系统中是如何应用的呢？这里概述下推荐系统中使用的常用思路。
RBM可以看做是一个编码解码的过程，从可见层到隐藏层就是编码，而反过来从隐藏层到可见层就是解码。在推荐系统中，我们可以把每个用户对各个物品的评分做为可见层神经元的输入，然后有多少个用户就有了多少个训练样本。由于用户不是对所有的物品都有评分，所以任意样本有些可见层神经元没有值。但是这不影响我们的模型训练。在训练模型时，对于每个样本，我们仅仅用有用户数值的可见层神经元来训练模型。
对于可见层输入的训练样本和随机初始化的、，我们可以用上面的sigmoid激活函数得到隐藏层的神经元的0,1值，这就是编码。然后反过来从隐藏层的神经元值和、可以得到可见层输出，这就是解码。对于每个训练样本， 我们期望编码解码后的可见层输出和我们的之前可见层输入的差距尽量的小，即上面的对数似然损失函数尽可能小。按照这个损失函数，我们通过迭代优化得到、、，然后对于某个用于那些没有评分的物品，我们用解码的过程可以得到一个预测评分，取最高的若干评分对应物品即可做用户物品推荐了。
如果大家对RBM在推荐系统的应用具体内容感兴趣，可以阅读参考文献3中的《Restricted Boltzmann Machines for Collaborative Filtering》

Restricted Boltzmann Machines for Collaborative Filtering.pdf

深度置信网络（DBN）

将若干个RBM“串联”起来则构成了一个DBN，其中，上一个RBM的隐层即为下一个RBM的显层，上一个RBM的输出即为下一个RBM的输入。训练过程中，需要充分训练上一层的RBM后才能训练当前层的RBM，直至最后一层。