python数据结构与算法 （一）未整理版

1.如何比较两个代码的快慢
O(1) 一个运算时间基本单位，大致理解为一个基础运算，例如+-*/print等等
时间复杂度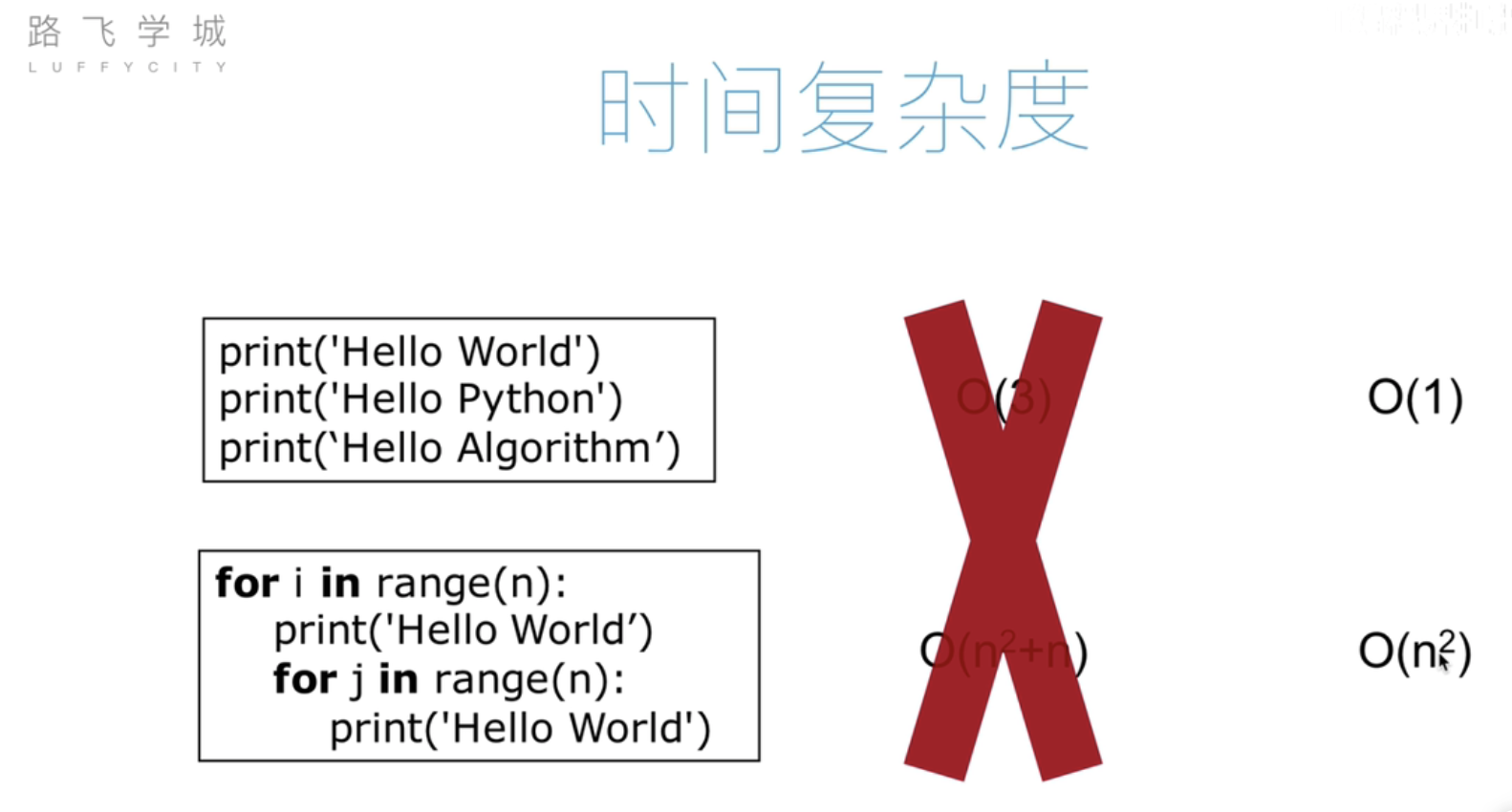
只考虑影响问题关键的，省略那些无关痛痒的

时间复杂度用来估算算法运算的时间。一边来说，时间复杂度越高，运算越慢。（相同运算内容，相同机器）
常见的时间复杂度（按效率排序）
O(1)快速地判断算法复杂度：
确定问题规模n
循环减半过程—->logn（2卫底）
K曾关于n的循环 —> n*k
复杂情况：根据算法执行过程判断
每层多少个参数 有多少层

空间复杂度：
用来评估算法内存占用的大小
表达方式与时间复杂度完全一样
算法使用了几个变量：O(1)
算法使用了长度为n的一位列表：O(n)
算法使用了m行n列的二位列表：O(mn)

宁可占用更多内存，也要更快
递归：
1.调用自身
2.结束条件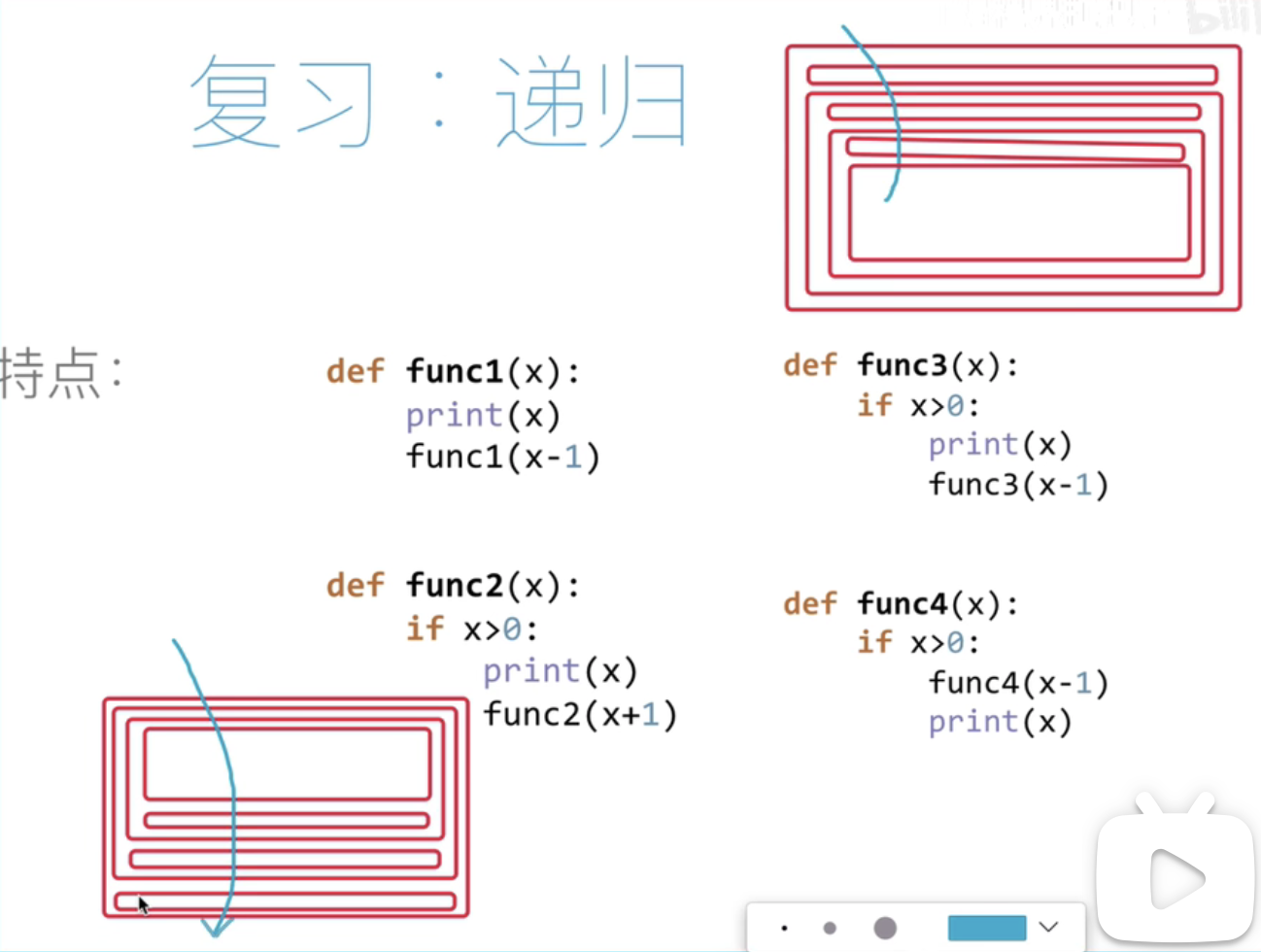

为什么打印顺序不同

汉诺塔问题：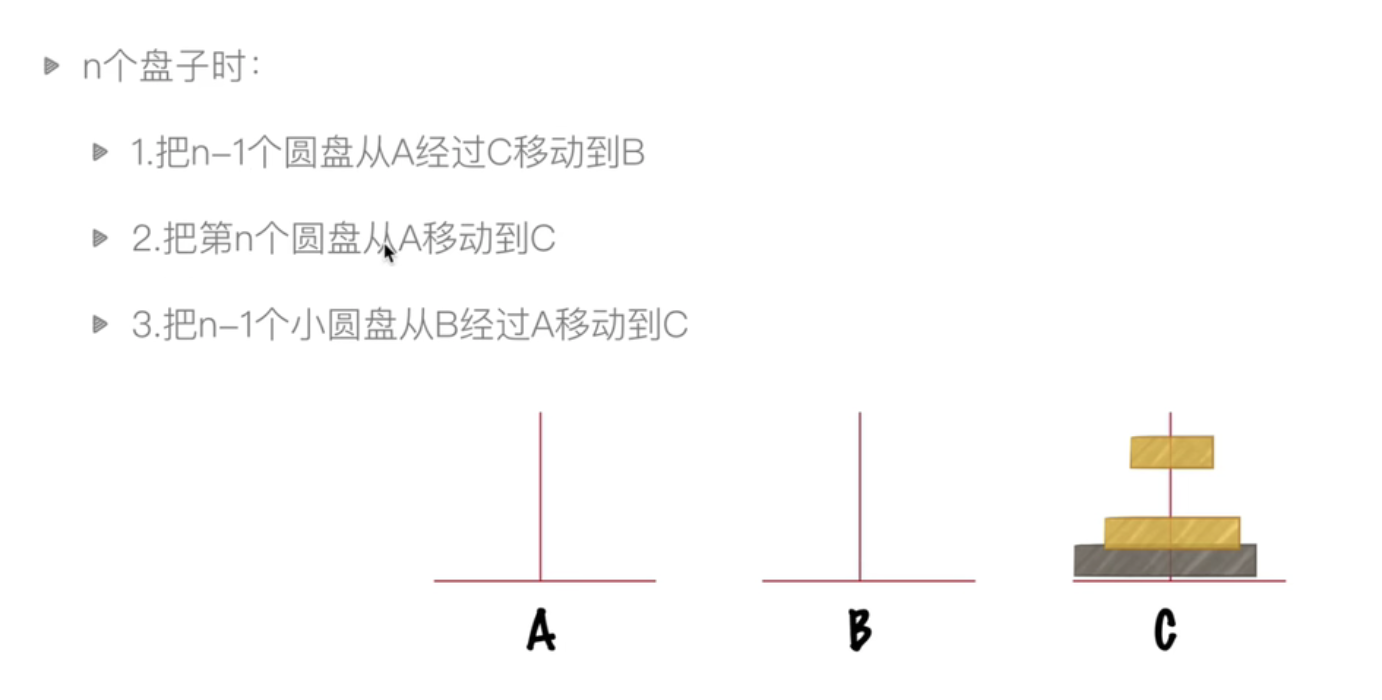

递推式：h（x) = h(x-1) + 1

def hanoi(n,a,b,c): # n:盘子个数 abc三个柱子，从a经过b移动到c
    if n>0:
        hanoi(n-1,a,c,b) ## n-1个盘子，从a经过c移动到b，因为下一步是最后一个盘子，由a移动到c
        print('moving for %s to %s' % (a,c))
        hanoi(n-1,b,a,c) ## n-1个盘子，从b经过a移动到c
hanoi(3,'A','B','C')

列表查找问题

1. 顺序查找

def linear_search(li,val):
    for ind,v in enumerate(li):
        if v == val:
            return ind
    else:
        return None

ps: enumerate() 函数用于将一个可遍历的数据对象(如列表、元组或字符串)组合为一个索引序列，同时列出数据和数据下标，一般用在 for 循环当中。
二分查找 Binary Search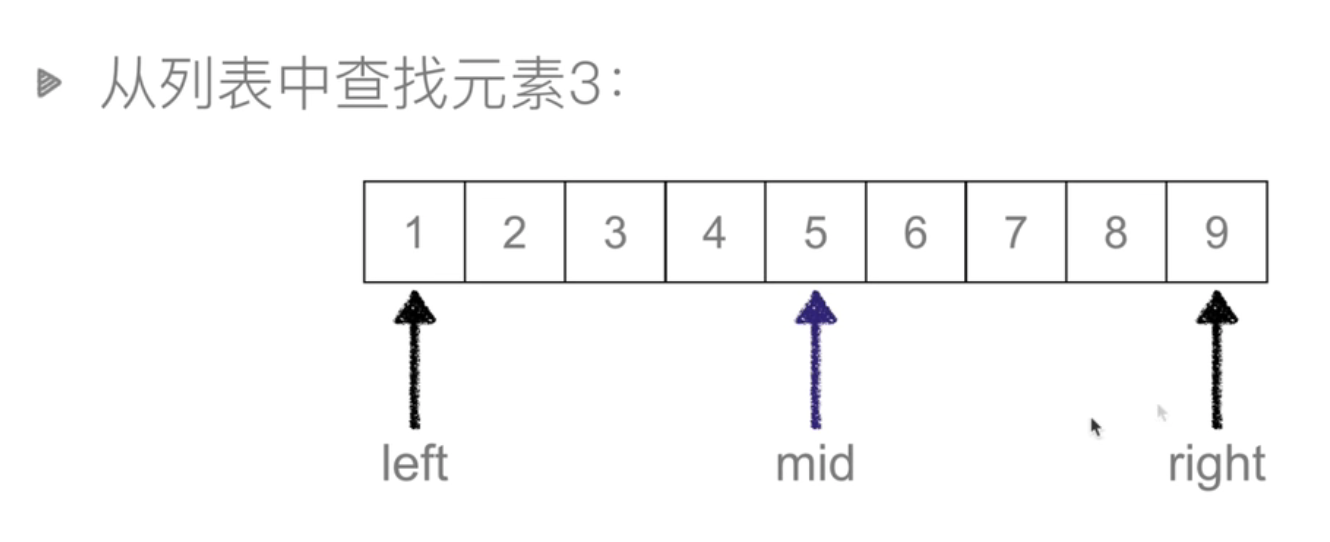

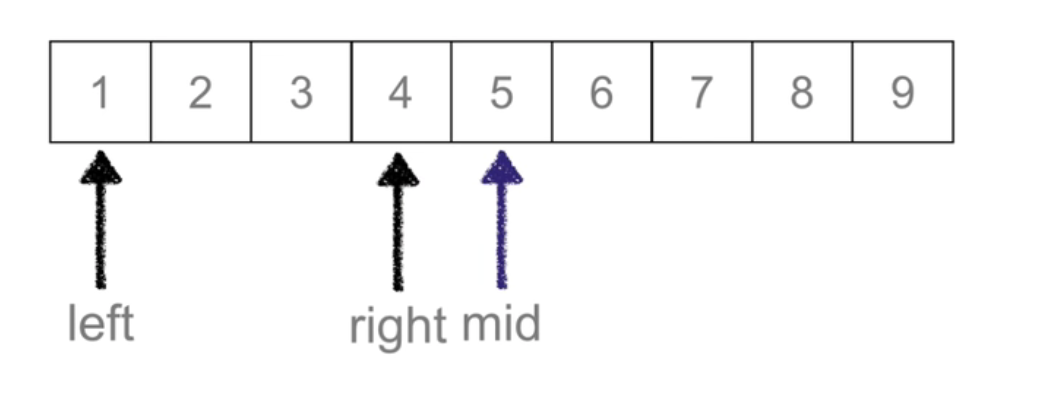
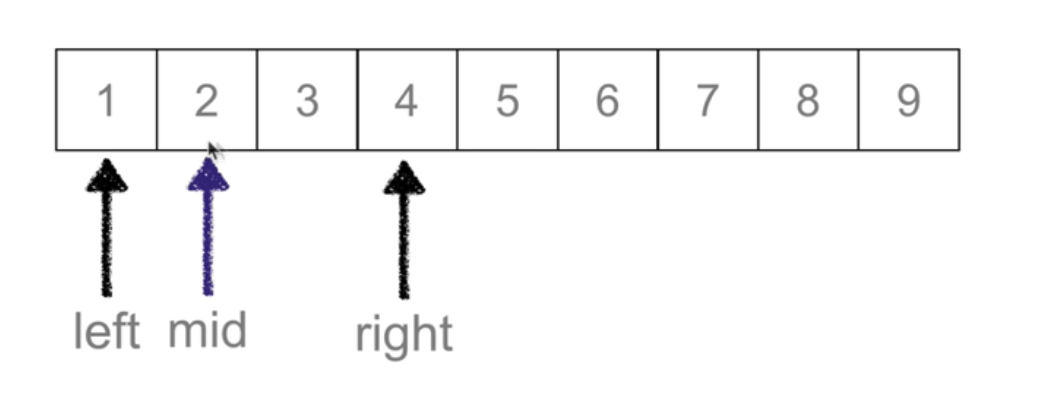
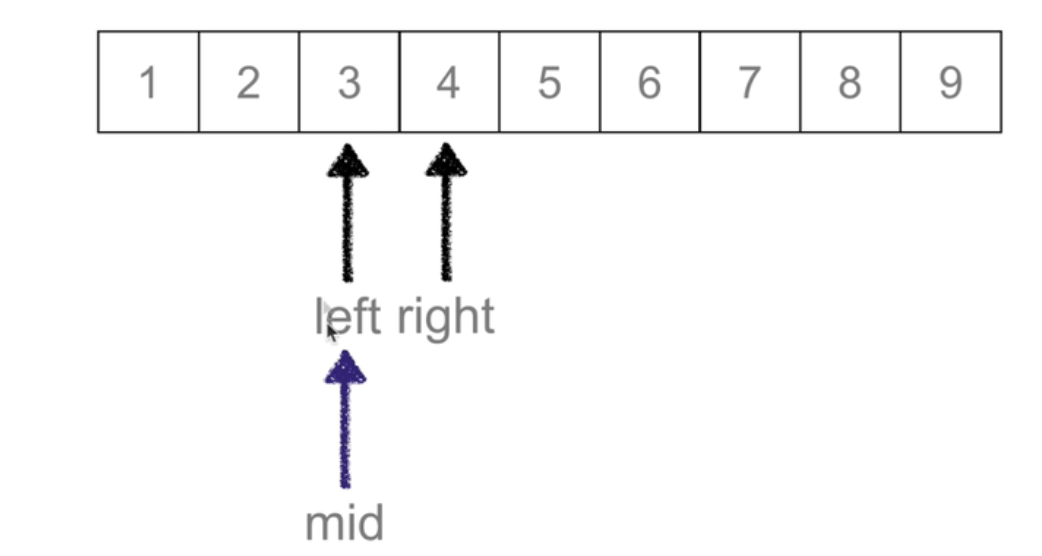
def binary_search(li,val):
    left =0
    right = len(li) - 1
    while left <= right: # 候选区有值
        mid =(left + right) //2
        if li[mid] == val:
            return mid
        elif li[mid] > val: ## 待查找值在mid左边
            right = mid-1
        elif li[mid] < val: #待查找值在mid右边
            left = mid +1
    else:
        return None
    ## keypoint： 不断移动左右边界，实现二分查找

时间复杂度： O(logn)
list 中的内置列表查找函数：index()是线性查找，因为列表不一定有序
排序的时间复杂度 大于O(n),所以自己权衡一下

排序

每蹚跳出一个无序区最大的数，跳入有序区
时间复杂度：O(n2), 原地排序

def bubble_sort(li):
    for i in range(len(li)-1): ## 第i趟
        for j in range(len(li)-i-1):
            if li[j] > li[j+1]:
                li[j],li[j+1] = li[j+1],li[j] ## list内部元组交换
import random
li = [random.randint(0,100) for i in range(100)]
print(li)
bubble_sort(li)
print(li)

改进：如果到第x趟时，已经排好了，就停止，不用跑完len(li)-1趟

def bubble_sort_de(li): ## 降序
    for i in range(len(li)-1):
        exchange = False
        for j in range(len(li)-i-1):
            if li[j] < li[j+1]:
                li[j], li[j + 1] = li[j + 1], li[j]
                exchange = True
        print(li)
        if not exchange:
            return
li = [6,5,4,3,2,1,7,8,9]
bubble_sort_de(li)
print(li)

1. 选择排序

没遍历一次，挑一个最大或最小值，排起来

def select_sort_simple(li):
    li_new=[]
    for i in range(len(li)):
        min_val = min(li)
        li_new.append(min_val)
        li.remove(min_val) 
        ## remove的操作，不是O1,而是On，因为要先找到，同理min，这两个此处是一个On 
    return li_new
## 生成了一个新list，废内存，占两个内存
## 复杂度 0（n2）
li = [3,2,4,1,5,6,8,9]
print(select_sort_simple(li))

改进：不新建list增加内存，采用交换

def slect_sort(li):
    for i in range(len(li)-1):
        min_loc = i # 无序区第一个数
        for j in range(i+1,len(li)): ## 能少算一个数就少算一个数
            if li[j] < li[min_loc]:
                min_loc = j
        li[i],li[min_loc] = li[min_loc],li[i]
        print(li)
li = [3,2,4,1,5,6,8,7,9]
print(li)
slect_sort(li)
## 复杂度：两层循环，O(n2)

插入排序：

对有序区不断排序

def insert_sort(li):
    for i in range(1,len(li)):  ## i表示摸到的牌的下标
        tmp = li[i]
        j = i -1 ## 手里的牌的细表
        while j >= 0 and li[j] > tmp:  # li[i]下表在变，所以要把值存起来
            li[j+1] = li[j] ## 手里的牌右移
            j -= 1 ## 指针左移
        li[j+1] = tmp
        print(li)
li = [3,2,4,1,5,6,8,7,9]
print(li)
insert_sort(li)
## 复杂度：两层循环，O(n2)

题外话：电脑一秒大约运算10**7