简介

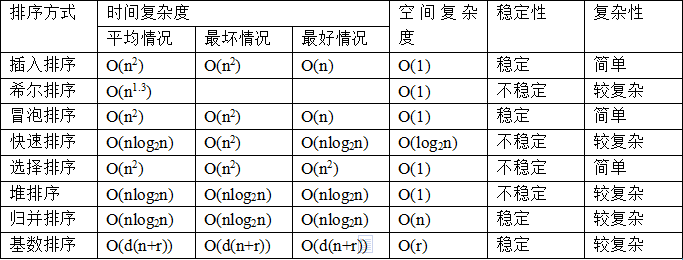
一、插入排序
　　每次将一个待排序的数据，跟前面已经有序的序列的数字一一比较找到自己合适的位置，插入到序列中，直到全部数据插入完成。

二、希尔排序
　　先将整个待排元素序列分割成若干个子序列（由相隔某个“增量”的元素组成的）分别进行直接插入排序，然后依次缩减增量再进行排序，待整个序列中的元素基本有序（增量足够小）时，再对全体元素进行一次直接插入排序。由于希尔排序是对相隔若干距离的数据进行直接插入排序，因此可以形象的称希尔排序为“跳着插”

三、冒泡排序
通过交换使相邻的两个数变成小数在前大数在后，这样每次遍历后，最大的数就“沉”到最后面了。重复N次即可以使数组有序。

冒泡排序改进1：在某次遍历中如果没有数据交换，说明整个数组已经有序。因此通过设置标志位来记录此次遍历有无数据交换就可以判断是否要继续循环。

冒泡排序改进2：记录某次遍历时最后发生数据交换的位置，这个位置之后的数据显然已经有序了。因此通过记录最后发生数据交换的位置就可以确定下次循环的范围了。

四、快速排序
“挖坑填数+分治法”，首先令i =L; j = R; 将a[i]挖出形成第一个坑，称a[i]为基准数。然后j—由后向前找比基准数小的数，找到后挖出此数填入前一个坑a[i]中，再i++由前向后找比基准数大的数，找到后也挖出此数填到前一个坑a[j]中。重复进行这种“挖坑填数”直到i==j。再将基准数填入a[i]中，这样i之前的数都比基准数小，i之后的数都比基准数大。因此将数组分成二部分再分别重复上述步骤就完成了排序。

五、选择排序
数组分成有序区和无序区，初始时整个数组都是无序区，然后每次从无序区选一个最小的元素直接放到有序区的最后，直到整个数组变有序区。

六、堆排序
图: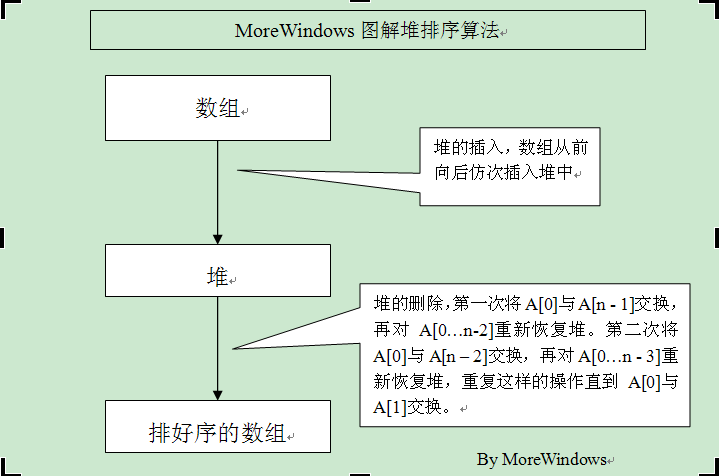


堆的插入就是——每次插入都是将新数据放在数组最后，而从这个新数据的父结点到根结点必定是一个有序的数列，因此只要将这个新数据插入到这个有序数列中即可。
堆的删除就是——堆的删除就是将最后一个数据的值赋给根结点，然后再从根结点开始进行一次从上向下的调整。调整时先在左右儿子结点中找最小的，如果父结点比这个最小的子结点还小说明不需要调整了，反之将父结点和它交换后再考虑后面的结点。相当于从根结点开始将一个数据在有序数列中进行“下沉”。
因此，堆的插入和删除非常类似直接插入排序，只不是在二叉树上进行插入过程。所以可以将堆排序形容为“树上插”

七、归并排序
归并排序主要分为两步：分数列（divide），每次把数列一分为二，然后分到只有两个元素的小数列；合数列（Merge），合并两个已经内部有序的子序列，直至所有数字有序。用递归可以实现。

八、基数排序（桶排序）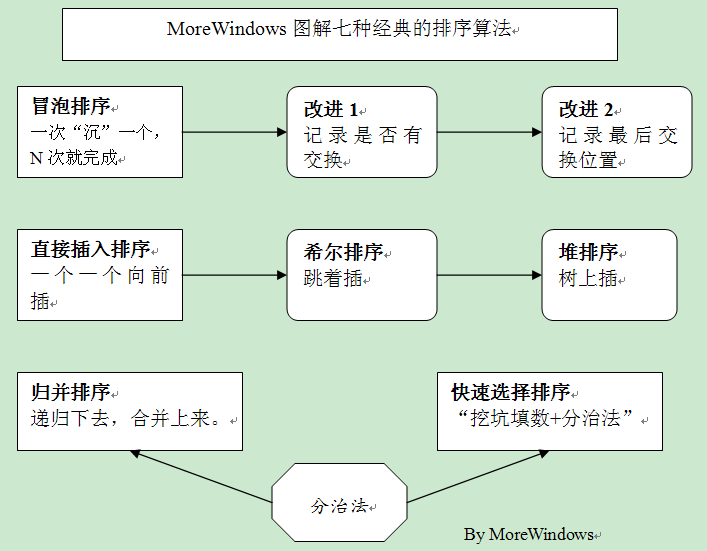

基数排序，第一步根据数字的个位分配到每个桶里，在桶内部排序，然后将数字再输出（串起来）；然后根据十位分桶，继续排序，再串起来。直至所有位被比较完，所有数字已经有序。

冒泡排序

package com.cheung.sort;
public class BubbleSorting {
    public static void main(String[] args) {
        int[] arr = new int[]{3,5,1,4,2,2,4};
        System.out.println("排序前");
        sout(arr);
        int[] sort = sort(arr);
        System.out.println("\n排序后");
        sout(sort);
    }
    public static int[] sort(int[] arr){
        for(int i = 0; i < arr.length; i++){
            Boolean flag = false;
            for(int j = 0; j < arr.length - i - 1; j++){
                if(arr[j] > arr[j+1]){
                    int temp = arr[j];
                    arr[j] = arr[j+1];
                    arr[j+1] = temp;
                    flag = true;
                }
            }
            if(flag == false){
                return arr;
            }
        }
        return arr;
    }
    public static void sout(int[] arr){
        for(int i = 0; i < arr.length; i++){
            System.out.printf("%d\t",arr[i]);
        }
    }
}

选择排序

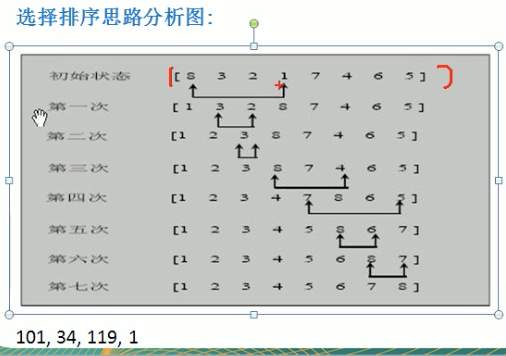
我直接开始写

package com.cheung.sort;

import java.util.Arrays;

public class SelectSorting {
    public static void main(String[] args) {
        int[] arr = new int[]{1,1,2,5,7};
        System.out.println("排序前");
        System.out.println(Arrays.toString(arr));
        int[] sort = SelectSort(arr);
        System.out.println("\n排序后");
        System.out.println(Arrays.toString(sort));

    }

    /**
     * 选择排序，第一次从数组选出最小值，交换到【0】 再从【1】-【n】选出最小值，交换。。
     * @param arr
     * @return
     */
    public static int[] SelectSort(int[] arr){
        for(int i = 0; i < arr.length - 1; i++){
            //通过一个循环找到从i开始到n的最小值
            int min = arr[i];//默认第一个最小
            int minSub = i;
            for(int j = i + 1; j < arr.length; j++){
                if(arr[j] < min){ //如果后后面的元素比我这个最小元素还小，min就是这个元素
                    min = arr[j];
                    minSub = j;
                }
            }
            //上面循环结束的时候，min就是最小值了
            arr[minSub] = arr[i];
            arr[i] = min;
        }
        return arr;
    }


}

插入排序

我们用逐步推倒的方式来学

package com.cheung.sort;

import java.util.Arrays;

public class InsertionSorting {
    public static void main(String[] args) {
        int[] arr = new int[]{101, 34, 119, 1};
        System.out.println("排序前");
        System.out.println(Arrays.toString(arr));
        int[] sort = InsertSort(arr);
        System.out.println("\n排序后");
        System.out.println(Arrays.toString(sort));
    }

    public static int[] InsertSort(int[] arr) {
        if(arr.length == 1){
            return arr;
        }
        //{101, 34, 119, 1}; ==》 {34, 101, 119, 1};

        for(int i = 1; i < arr.length; i++){
            //定义待插入待数
            int insertVal = arr[i];
            int insertIndex = i - 1; //待插入序列的索引

            //给切片找插入位置
            //1 insertIndex >= 0保证再给insertVal切片找插入位置的时候不越界
            //2.insertVal < arr[insertIndex] 待插入的数，还没有找到插入位置
            //3.就需要将arr[insertIndex]后移
            while(insertIndex >= 0 && insertVal < arr[insertIndex]){
                arr[insertIndex + 1] = arr[insertIndex];
                insertIndex--;
            }
            //当退出while循环时，说明插入的位置找到，insertIndex + 1
            arr[insertIndex + 1] = insertVal;
        }
        return arr;
    }
}

希尔排序

快速排序

归并排序

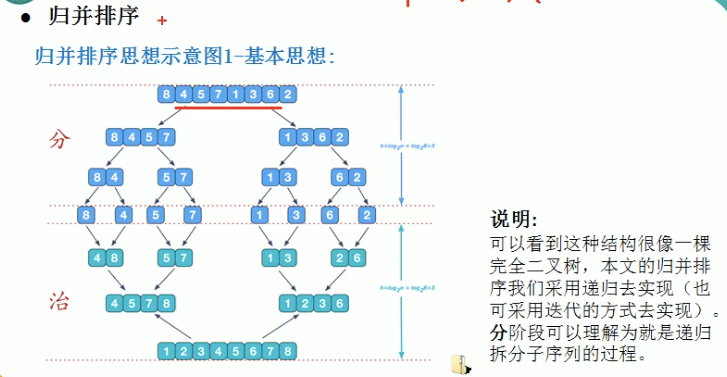
package com.cheung.sort;

import java.util.Arrays;

public class MergeSorting {
    public static void main(String[] args) {
        int[] arr = new int[]{8, 4, 5, 7, 1, 3, 6, 2};
        int[] temp = new int[arr.length]; //归并排序需要一个额外的空间
        System.out.println("并归排序前");
        System.out.println(Arrays.toString(arr));
        mergeSort(arr,0,arr.length - 1,temp);
        System.out.println("并归排序后");
        System.out.println(Arrays.toString(arr));
    }

    //分 + 合 方法
    public static void mergeSort(int[] arr, int left, int right, int[] temp){
        if(left < right){
            int mid = (left + right) / 2; //中间索引
            //向左递归进行分解
            mergeSort(arr,left,mid,temp);
            //向右递归进行分解
            mergeSort(arr,mid+1,right,temp);
            //到合并
            merge(arr,left,mid,right,temp);
        }
    }

    //合并的方法
    /**
     *
     * @param arr  待排序的原始数组
     * @param left 左边有序序列的初始索引
     * @param mid 中间索引
     * @param right 右边索引
     * @param temp 做中转的索引
     */
    public static void merge(int[] arr,int left, int mid, int right, int[] temp){
        int i = left; //初始化i，左边有序序列的初始索引
        int j = mid + 1;  //初始化j，右边有序序列的初始索引
        int t = 0; //指向temp数组的当前索引

        //（一）
        //先把左右两边（有序）的数据按照规则填充到temp数组
        //直到左右两边的有序序列，有一边处理完毕为止
        while(i <= mid  && j <= right){  //继续
            if(arr[i] <= arr[j]){   //左边当前元素小于等于右边有序序列的当前元素
                temp[t] = arr[i];
                t += 1;
                i += 1;
            }else { //右边小
                temp[t] = arr[j];
                t += 1;
                j += 1;
            }
        }

        //（二）
        //把有剩余的数据的一边的数据依次全部填充到temp去
        while(i <= mid){
            temp[t] = arr[i];
            t += 1;
            i += 1;
        }
        while(j <= right){
            temp[t] = arr[j];
            t += 1;
            j += 1;
        }

        //（三）
        //将temp数组的元素拷贝到arr
        //注意，并不是每一次都拷贝所有
        t = 0;
        int tempLeft = left; //
        while(tempLeft <= right){ //第一次合并tempLeft = 0, right = 1 | 第二次合并tempLeft = 2, right = 3 | 第三次合并 0 3 ｜
            // 最后一次0 7
            arr[tempLeft] = temp[t];
            t += 1;
            tempLeft += 1;
        }
    }
}