树

树是一种数据结构，它是n(n>=0)个节点的有限集。n=0时称为空树。n>0时，有限集的元素构成一个具有层次感的数据结构
[

](https://www.pdai.tech/md/algorithm/alg-basic-tree.html)
区别于线性表一对一的元素关系，树中的节点是一对多的关系。树具有以下特点:

n>0时，根节点是唯一的，不可能存在多个根节点。
每个节点有零个至多个子节点；除了根节点外，每个节点有且仅有一个父节点。根节点没有父节点。

树的相关概念

子树：除了根节点外，每个子节点都可以分为多个不相交的子树
孩子和双亲：若一个结点有子树，那么该结点称为子树根的”双亲”，子树的根是该结点的”孩子”。在图一中，B、H是A的孩子，A是B、H的双亲
兄弟: 具有相同双亲的节点互为兄弟，例如B与H互为兄弟。
节点的度: 一个节点拥有子树的数目。例如A的度为2，B的度为1，C的度为3.
叶子: 没有子树，也即是度为0的节点。
分支节点: 除了叶子节点之外的节点，也即是度不为0的节点。
内部节点: 除了根节点之外的分支节点。
层次: 根节点为第一层，其余节点的层次等于其双亲节点的层次加1.
树的高度: 也称为树的深度，树中节点的最大层次。
有序树: 树中节点各子树之间的次序是重要的，不可以随意交换位置。
无序树: 树种节点各子树之间的次序是不重要的。可以随意交换位置。
森林: 0或多棵互不相交的树的集合。例如图二中的两棵树为森林

二叉树

最多有两棵子树的树被称为二叉树

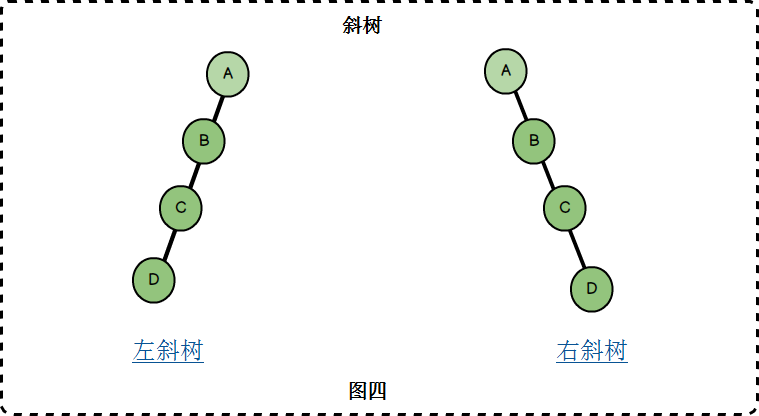
斜树:

所有节点都只有左子树的二叉树叫做左斜树，所有节点都只有右子树的二叉树叫做右斜树。(本质就是链表)

满二叉树

二叉树中所有非叶子结点的度都是2，且叶子结点都在同一层次上

完全二叉树

如果一个二叉树与满二叉树前m个节点的结构相同，这样的二叉树被称为完全二叉树

二叉查找树 - BST

二叉查找树(Binary Search Tree)是指一棵空树或者具有下列性质的二叉树:
若任意节点的左子树不空，则左子树上所有节点的值均小于它的根节点的值；
若任意节点的右子树不空，则右子树上所有节点的值均大于它的根节点的值；
任意节点的左、右子树也分别为二叉查找树；
没有键值相等的节点。