目录
三、神经网络
- 定义网络

作者：Soumith Chintala

原文翻译自：https://pytorch.org/tutorials/beginner/deep_learning_60min_blitz.html

中文翻译、注释制作：黄海广

github：https://github.com/fengdu78

代码全部测试通过。

配置环境：PyTorch 1.0，python 3.6，

主机：显卡：一块1080ti；内存：32g（注：绝大部分代码不需要GPU）

三、神经网络

可以使用torch.nn包来构建神经网络.

你已知道autograd包,nn包依赖autograd包来定义模型并求导.一个nn.Module包含各个层和一个forward(input)方法,该方法返回output.

例如,我们来看一下下面这个分类数字图像的网络.

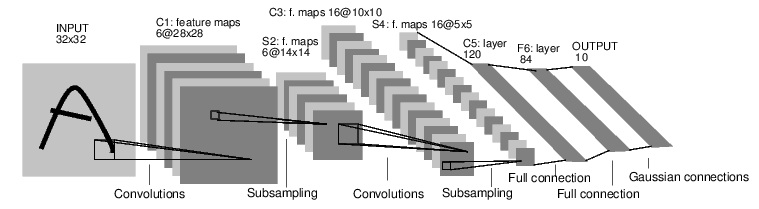
他是一个简单的前馈神经网络,它接受一个输入,然后一层接着一层的输入,直到最后得到结果。

神经网络的典型训练过程如下:

定义神经网络模型,它有一些可学习的参数(或者权重);
在数据集上迭代;
通过神经网络处理输入;
计算损失(输出结果和正确值的差距大小)
将梯度反向传播会网络的参数;
更新网络的参数,主要使用如下简单的更新原则:weight = weight - learning_rate * gradient

定义网络

我们先定义一个网络：

import torch
import torch.nn as nn
import torch.nn.functional as F
class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        # 1 input image channel, 6 output channels, 5x5 square convolution
        # kernel
        self.conv1 = nn.Conv2d(1, 6, 5)
        self.conv2 = nn.Conv2d(6, 16, 5)
        # an affine operation: y = Wx + b
        self.fc1 = nn.Linear(16 * 5 * 5, 120)
        self.fc2 = nn.Linear(120, 84)
        self.fc3 = nn.Linear(84, 10)
    def forward(self, x):
        # Max pooling over a (2, 2) window
        x = F.max_pool2d(F.relu(self.conv1(x)), (2, 2))
        # If the size is a square you can only specify a single number
        x = F.max_pool2d(F.relu(self.conv2(x)), 2)
        x = x.view(-1, self.num_flat_features(x))
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        x = self.fc3(x)
        return x
    def num_flat_features(self, x):
        size = x.size()[1:]  # all dimensions except the batch dimension
        num_features = 1
        for s in size:
            num_features *= s
        return num_features
net = Net()
print(net)

Net(
  (conv1): Conv2d(1, 6, kernel_size=(5, 5), stride=(1, 1))
  (conv2): Conv2d(6, 16, kernel_size=(5, 5), stride=(1, 1))
  (fc1): Linear(in_features=400, out_features=120, bias=True)
  (fc2): Linear(in_features=120, out_features=84, bias=True)
  (fc3): Linear(in_features=84, out_features=10, bias=True)
)

你只需定义forward函数,backward函数(计算梯度)在使用autograd时自动为你创建.你可以在forward函数中使用Tensor的任何操作。

net.parameters()返回模型需要学习的参数。

params = list(net.parameters())
print(len(params))
print(params[0].size())

10
torch.Size([6, 1, 5, 5])

forward的输入和输出都是autograd.Variable.注意:这个网络(LeNet)期望的输入大小是3232.如果使用MNIST数据集来训练这个网络,请把图片大小重新调整到3232.

input = torch.randn(1, 1, 32, 32)
out = net(input)
print(out)

tensor([[-0.1217,  0.0449, -0.0392, -0.1103, -0.0534, -0.1108, -0.0565,  0.0116,
          0.0867,  0.0102]], grad_fn=<AddmmBackward>)

将所有参数的梯度缓存清零,然后进行随机梯度的的反向传播.

net.zero_grad()
out.backward(torch.randn(1, 10))

注意
torch.nn 只支持小批量输入,整个torch.nn包都只支持小批量样本,而不支持单个样本
例如,nn.Conv2d将接受一个4维的张量,每一维分别是 $60分钟入门深度学习工具-PyTorch(三、神经网络) - 图2$ (样本数通道数高*宽).
如果你有单个样本,只需使用input.unsqueeze(0)来添加其它的维数.

在继续之前,我们回顾一下到目前为止见过的所有类.

回顾

torch.Tensor-支持自动编程操作（如backward()）的多维数组。同时保持梯度的张量。
nn.Module-神经网络模块.封装参数,移动到GPU上运行,导出,加载等
nn.Parameter-一种张量,当把它赋值给一个Module时,被自动的注册为参数.
autograd.Function-实现一个自动求导操作的前向和反向定义, 每个张量操作都会创建至少一个Function节点，该节点连接到创建张量并对其历史进行编码的函数。

现在,我们包含了如下内容:

定义一个神经网络
处理输入和调用backward

剩下的内容:

计算损失值
更新神经网络的权值

损失函数

一个损失函数接受一对(output, target)作为输入(output为网络的输出,target为实际值),计算一个值来估计网络的输出和目标值相差多少。

在nn包中有几种不同的损失函数.一个简单的损失函数是:nn.MSELoss,它计算输入和目标之间的均方误差。

例如:

output = net(input)
target = torch.randn(10)  # a dummy target, for example
target = target.view(1, -1)  # make it the same shape as output
criterion = nn.MSELoss()
loss = criterion(output, target)
print(loss)

tensor(0.5663, grad_fn=<MseLossBackward>)

现在,你反向跟踪loss,使用它的.grad_fn属性,你会看到向下面这样的一个计算图:

input -> conv2d -> relu -> maxpool2d -> conv2d -> relu -> maxpool2d
-> view -> linear -> relu -> linear -> relu -> linear
-> MSELoss
-> loss

所以, 当你调用loss.backward(),整个图被区分为损失以及图中所有具有requires_grad = True的张量，并且其.grad 张量的梯度累积。

为了说明,我们反向跟踪几步:

print(loss.grad_fn)  # MSELoss
print(loss.grad_fn.next_functions[0][0])  # Linear
print(loss.grad_fn.next_functions[0][0].next_functions[0][0])

<MseLossBackward object at 0x0000029E54C509B0>
<AddmmBackward object at 0x0000029E54C50898>
<AccumulateGrad object at 0x0000029E54C509B0>

反向传播

为了反向传播误差,我们所需做的是调用loss.backward().你需要清除已存在的梯度,否则梯度将被累加到已存在的梯度。

现在,我们将调用loss.backward(),并查看conv1层的偏置项在反向传播前后的梯度。

net.zero_grad()     # zeroes the gradient buffers of all parameters
print('conv1.bias.grad before backward')
print(net.conv1.bias.grad)
loss.backward()
print('conv1.bias.grad after backward')
print(net.conv1.bias.grad)

conv1.bias.grad before backward
tensor([0., 0., 0., 0., 0., 0.])
conv1.bias.grad after backward
tensor([ 0.0006, -0.0164,  0.0122, -0.0060, -0.0056, -0.0052])

稍后阅读:

神经网络包包含了各种用来构成深度神经网络构建块的模块和损失函数,一份完整的文档查看这里

唯一剩下的内容:

更新网络的权重

更新权重

实践中最简单的更新规则是随机梯度下降(SGD)．

weight=weight−learning_rate∗gradient

我们可以使用简单的Python代码实现这个规则。

learning_rate = 0.01
for f in net.parameters():
    f.data.sub_(f.grad.data * learning_rate)

然而,当你使用神经网络是,你想要使用各种不同的更新规则,比如SGD,Nesterov-SGD,Adam, RMSPROP等.为了能做到这一点,我们构建了一个包torch.optim实现了所有的这些规则.使用他们非常简单:

import torch.optim as optim
# create your optimizer
optimizer = optim.SGD(net.parameters(), lr=0.01)
# in your training loop:
optimizer.zero_grad()   # zero the gradient buffers
output = net(input)
loss = criterion(output, target)
loss.backward()
optimizer.step()    # Does the update

注意

观察如何使用optimizer.zero_grad()手动将梯度缓冲区设置为零。这是因为梯度是反向传播部分中的说明那样是累积的。

本章的官方代码：

Python：neural_networks_tutorial.py
Jupyter notebook:neural_networks_tutorial.ipynb

60分钟入门深度学习工具-PyTorch(三、神经网络)

目录