傅里叶基础知识

从数学角度来讲：傅里叶变换将一个任意的周期函数分解成为无穷个正弦函数的和的形式。
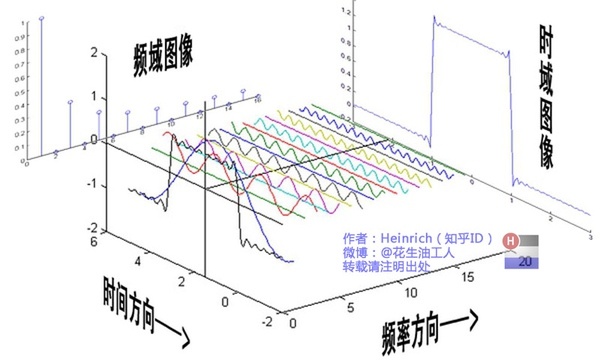
从物理角度来讲：傅里叶变换实现了将信号从空间域到频率域的转换。时域和频域的表述是互逆的
法国数学家吉恩·巴普提斯特·约瑟夫·傅里叶被世人铭记的最大的贡献是：他指出任何周期函数都可以表示为不同频率的正弦和/或余弦之和的形式，每个正弦项和/或余弦项乘以不同的系数（现在称该和为傅里叶级数）。无论函数多么复杂，只要它是周期的，并且满足某些适度的数学条件，都可以用这样的和来表示。即一个复杂的函数可以表示为简单的正弦和余弦之和。甚至非周期函数（单该曲线下的面积是有限的）也可以用正弦和/或许·余弦乘以加权函数的积分来表示。在这种情况下的公式就是傅里叶公式。

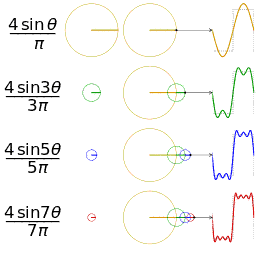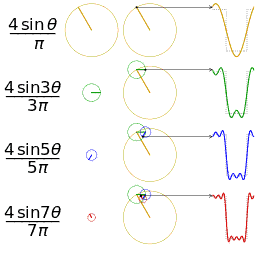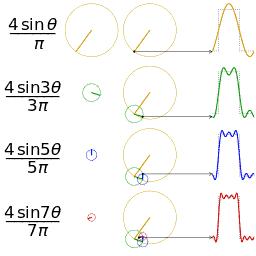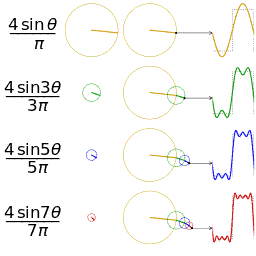
傅里叶基础numpy实现

• 傅里叶得到低频、高频信息，针对低频、高频处理能够实现不同的 目的。
• 傅里叶过程是可逆的，图像经过傅里叶变换、逆傅里叶变换后，能 够恢复到原始图像
• 在频域对图像进行处理，在频域的处理会反映在逆变换图像上

img = cv2.imread('image\\lena.bmp',0)
f = np.fft.fft2(img)
fshift = np.fft.fftshift(f)
result = 20*np.log(np.abs(fshift))

关键函数：
傅里叶变换：numpy.fft.ifft2
傅里叶逆变换：numpy.fft.ifftshift

高通低通滤波

低频对应图像内变化缓慢的灰度分量。例如，在一幅大草原的图像中，低频对应着广袤的颜色趋于一致的草原。
高频对应图像内变化越来越快的灰度分量，是由灰度的尖锐过渡造成的。例如，在一幅大草原的图像中，其中狮子的边缘等信息。
滤波就是过滤掉不需要的部分。
通过低频的滤波器称为低通滤波器。
通过高频的滤波器称为高通滤波器

修改傅里叶变换以达到特殊目的，然后计算IDFT返回到图像域。比如我们可以利用傅里叶变换进行，图像增强、图像去噪、边缘检测、特征提取、图像压缩、图像加密等。
衰减高频而通过低频，低通滤波器，将模糊一幅图像。
衰减低频而通过高频，高通滤波器，将增强尖锐的细节，但是会导致图像的对比度降低

那么我们只需要再滤波中来一个掩膜操作，用高通滤波器去掉了低频，可以把边缘描绘得很完整，但对比度降低