获取图像->去噪（滤波、阈值化之类）->边缘检测->提取固定区域->给出目标点坐标

在图像的模糊中，滤波分为线性滤波、非线性滤波和形态学滤波。
图像处理中的操作步骤——先模糊、再锐化，模糊是为了提高信噪比，而锐化是为了突出图像边缘、 便于最后提取目标区域。

关于图像滤波

一般图像的能量主要集中在其低频部分，而图像的边缘部分以及噪声主要分布在高频部分。
图像的“模糊”就是对图像进行平滑处理，削弱其高频部分（目的是去除高频部分中的噪声），但是这同时也会模糊图像的边缘信息；而图像的“锐化”则是为了使图像的边缘、轮廓变得清晰，便于提取图像中需要的特征。我们进行图像的模糊与锐化的目的就是——提高信噪比，便于最后的特征提取的处理

通常所说的“滤波”指的是对图像的平滑处理（就是图像的模糊），也就是低通滤波；如果指的是图像的锐化，一般来说会强调是“高通”滤波。

邻域运算

是指当输出图象中每个像素是由对应的输入像素及其一个邻域内的像素共同决定时的图像运算。即 输出图像中的像素点由输入图像中的相应位置的像素点及其周围的像素点进行一些奇奇怪怪的运算得到。
而线性运算就是算子做加权求和的运算，用到的运算方式就是加减乘除之类；而非线性运算则不止使用简单的基本运算，还包括逻辑运算（比如位运算）、求最大值最小值、中值操作等等不能通过简单的基本运算法则而得到的运算。

线性邻域运算包括相关运算与卷积运算两种
相关运算就是将输入图像的对应像素点与掩膜作“加权求和”运算，并将运算结果填入输出图像中的”锚点“中。在OpenCV的几乎所有函数中，让你填锚点的地方，如果锚点填写负值，则表示锚点取卷积核的中央（这也很容易理解嘛，就是以输入图像中对应位置的那个像素点为中心，取邻域算子的范围）；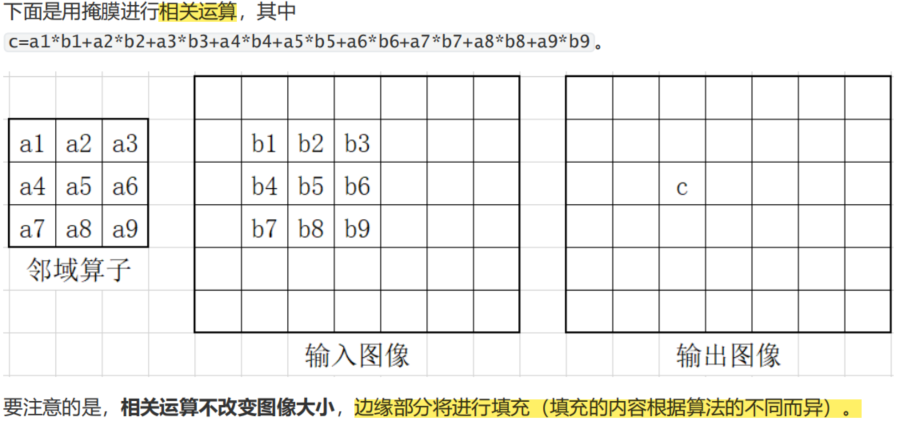
image.png

卷积运算则要稍微复杂一些，先要将卷积核进行180°的旋转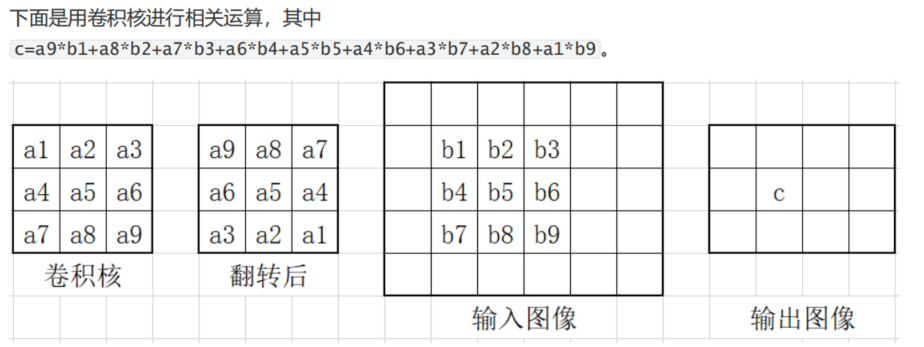
image.png
可以看到，卷积运算会改变图像大小，因为卷积运算不会对图像的边缘部分进行填充——但是图像处理中进行的卷积运算一般都是先进行填充再进行卷积的，因此如果你调用OpenCV中的相关函数，你会发现图像大小并没有改变。

线性滤波

方框滤波

主要函数：boxFilter。
⚽️运行结果=cv2. boxFilter(原始图像，目标图像深度，核大小，normalize属性)，
⚽️其中原始图像都理解，⚽️目标图像深度通常设置成-1，表示与原始图像相同，
⚽️normalize属性表示是否对图像进行归一化处理，如果进行归一化处理就设置成ture，不设置就为false。
⚽️那么如果设置归一化处理的结果就是与均值滤波完全一致，如果不设置归一化处理，那么就表示核函数之间相加。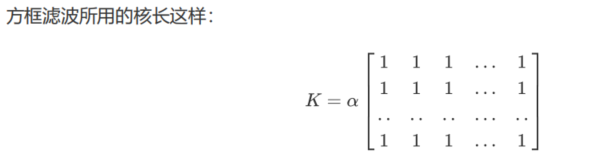


image.png
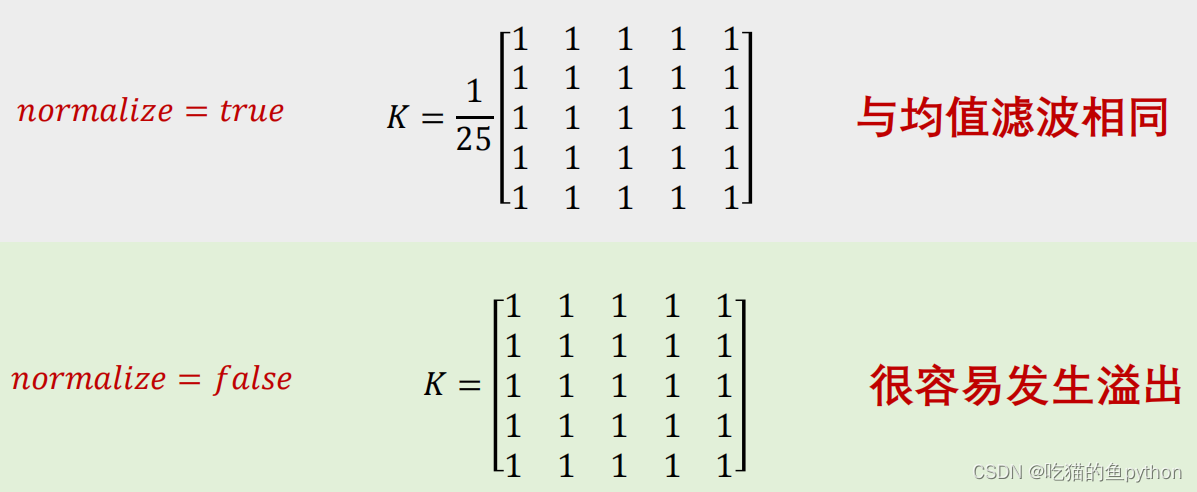
bec725c659804ed48913c2eb1481ca10.png
normalize=1就表示进行归一化处理，和不设置一样，也就是说默认就是进行归一化处理。如果设置为0，就表示不进行归一化处理。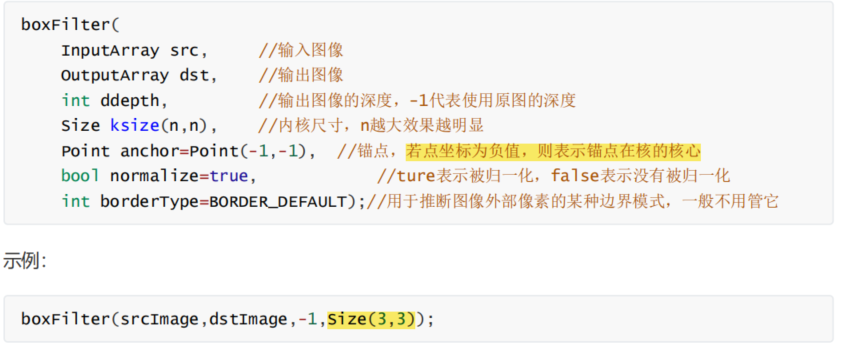
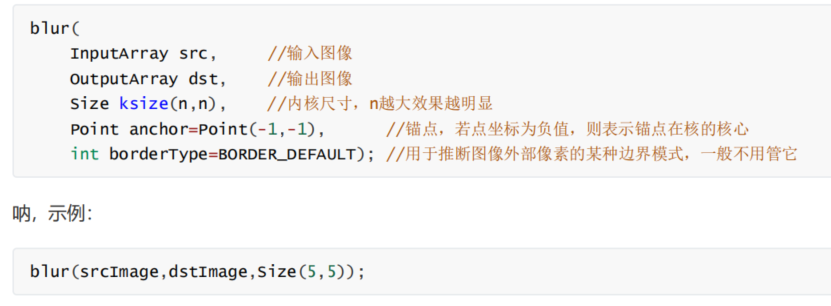
image.png

均值滤波

均值滤波也称为线性滤波，其主要的方法理念是建立一个滤波模板，该滤波模板取数字图像中的一个点的像素值，以该点为中心点，对该点周围的一个 33或者 55 的邻域矩阵做矩阵所有元素的均值替换中心值操作，这样求得的值更接近像素的真实值，从而消除图像中的噪声点。均值滤波对线性噪声的抑制效果比较好，但对非线性噪点影响不大，因为在修复噪点的同时会使图像分辨率降低，从而使图像过于模糊，使其噪点复原不够彻底。因为椒盐噪点是非线性的噪点，所以均值滤波对低密度椒盐噪点的滤波效果还可以，但对高密度椒盐噪点的滤波效果就不太理想了。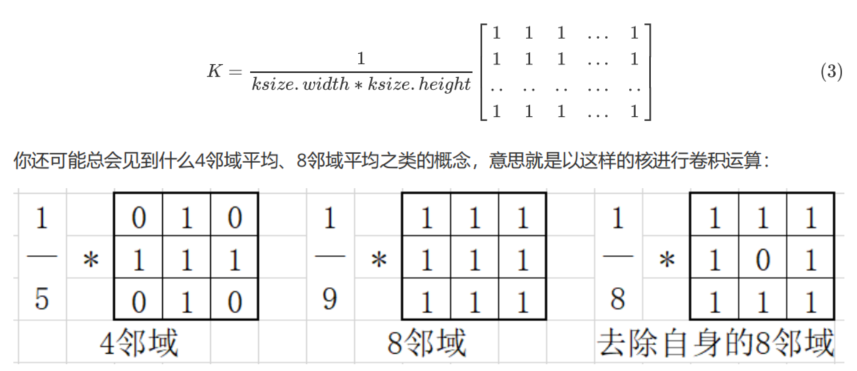
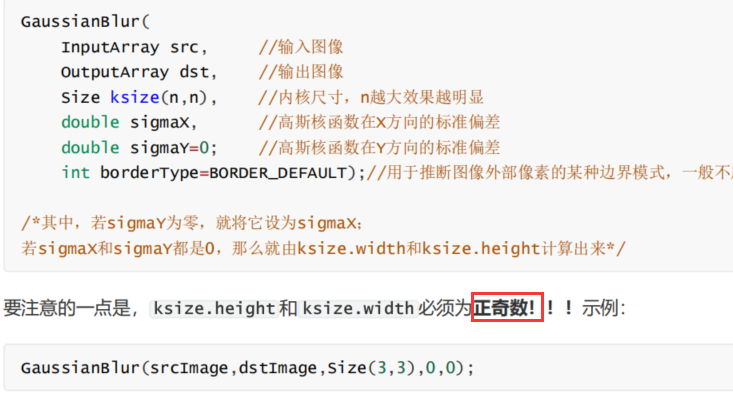
image.png
image.png

高斯滤波

高斯滤波就是利用正态分布的算子和图像进行卷积的过程，也称高斯模糊。
原理就是谁离我目标点越近，我就跟谁越好，给他的东西越多，对应官方的话就是给予权重越大。让临近的像素值有更高的重要度。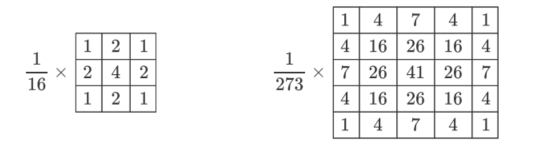
image.pngimage.png

非线性滤波

如果图像中的噪声不是高斯噪声，而是散粒噪声（意思就是存在一些像素点的值远远高于或低于周围像素点的值），这个时候线性滤波的弊端就体现出来了——线性滤波无法排除“极端值”对于图像的影响，即图像中的散粒噪声无法通过线性滤波而去除。

中值滤波

我们取了核函数的大小，然后把核函数中的像素值进行排序，然后取中值替换到现在的值。
在图像处理中，如果在邻域运算中采用“中值滤波”操作，能够排除极端值的干扰，也就是能够消除散粒噪声。不仅如此，中值滤波还能够克服线性滤波模糊图像边缘的缺点，能够比较好的保留图像边缘信息。
缺点是慢，需要内排序
image.png
ksize 只能填大于1的奇数

双边滤波

引入双边滤波里的两个权重域的概念：空间域（spatial domain S）和像素范围域（range domain R），分别受空间权重与相似权重的影响。
空间权重与像素位置有关，为像素之间的距离（欧式距离，空间度量）；相似权重与像素值大小有关，为像素值之间的距离（辐射距离，相似性度量）。意思就是，从两个不同的角度来分析——一个是像素点之间隔得多远，一个是邻域像素之间相差有多大。
双边滤波就是由空间域与像素范围域共同影响所得到的滤波效果——当空间权重远大于相似权重时（也就是邻域内基本只受空间距离的影响下），双边滤波的效果就基本类似于高斯滤波，都由高斯函数主要决定算子的权值，这样就能有效去除低频噪声；
但在图像的边缘地区，这时候相似权重的比重加大（因为像素点之间的差异大了嘛），因此能够很好地保留图像的边缘信息，不至于使在高斯滤波中一样将边缘模糊掉。
但是因为双边滤波会很好地保留图像的边缘信息——因此，随之带来的缺点就是，高频噪声无法被有效消除（毕竟边缘信息与高频噪声都处于高频段）。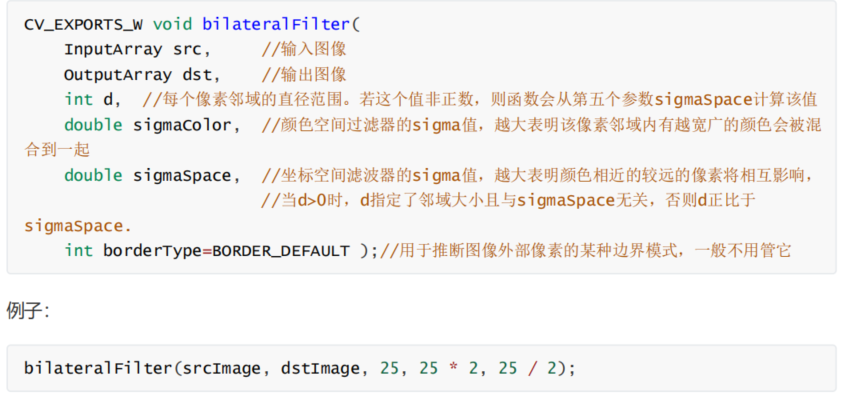
image.png

太慢了，最慢的滤波