神经元细胞模型
神经网络由基本的神经元组成，而每个神经元的具体结构是我们所需要关心的。一个简单的神经元结构如下图所示：<br />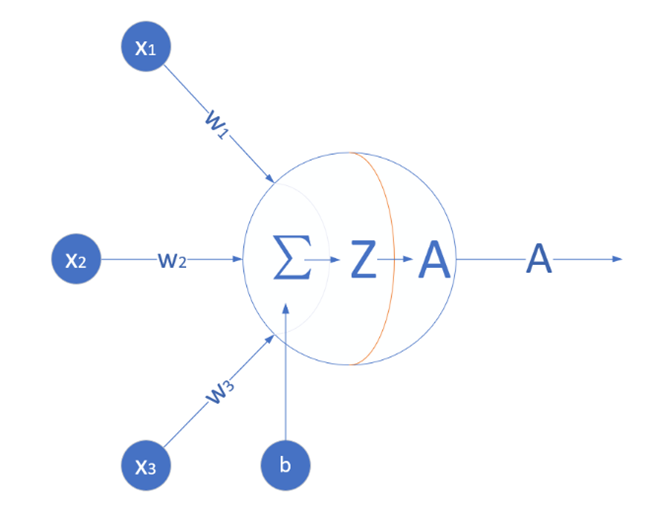<br />神经元的基本结构可分成5个基本部分：
输入
(x1,x2,x3) :外界输入信号，一般是一个训练数据样本的多个属性
权重
(w1,w2,w3):每个输入信号的权重值
偏移-b 使得神经元兴奋的临界值
- 求和计算
Z = W ⋅ X + b
- 激活函数
A=σ(Z)：阶跃信号，表示神经元向后传递信号的强度。用于将线性方程非线性化
由此，可对神经元的结构特点总结如下：
- 一个神经元可以有多个输入。
- 一个神经元只能有一个输出，这个输出可以同时输入给多个神经元。
- 一个神经元的w的数量和输入的数量一致。
- 一个神经元只有一个b。
- w和b有人为的初始值，在训练过程中被不断修改。
- A可以等于Z，即激活函数不是必须有的。
-
神经网络训练过程
一个简单的神经网络的训练过程可由下图进行描述：
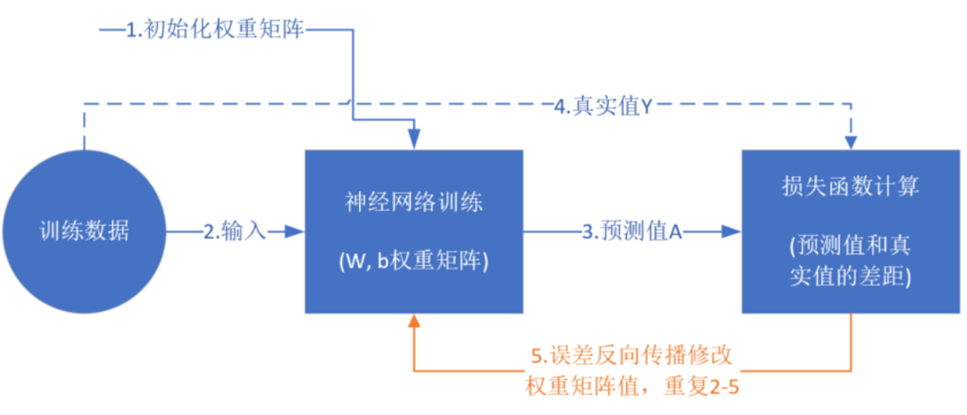
首先，对神经网络的权重矩阵进行初始化。之后，将训练数据或经处理的训练数据输入到神经网络当中。通过运算得出当前神经网络下的预测值，并与真实值进行比对，计算损失函数。最后将误差反向传播，对神经网络中的权重矩阵进行修正。神经网络主要功能
神经网络的主要功能大体上可分为如下两类：
回归/拟合：给出输入值，得出输出值的过程
- 分类：在数据中，根据类别划定分界线
激活函数
如果将一个神经网络类比于人的身体构造的话，那么激活函数类比于人体的关节就再合适不过了。激活函数本身是用来表示神经元向后传递信号的强度的，它的存在使得神经网络富有了极强的灵活性。激活函数的主要作用是使得神经网络原有的线性结构变为更加适合解决复杂问题的非线性结构。
若有收获，就点个赞吧
0 人点赞
