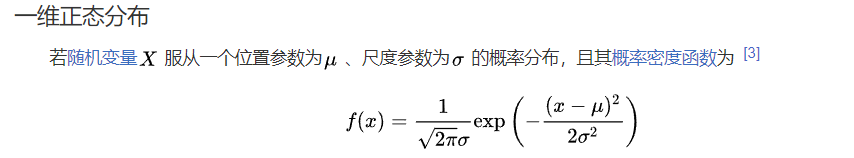前置数学背景：

image.png
参数重整化这个操作的好处说白了点就是 如果直接采样，会导致梯度不可导，这在神经网络中不利于梯度传播
所以可以用上述操作
KL散度详解可参见： https://zhuanlan.zhihu.com/p/365400000
高斯分布的KL散度可参见：https://blog.csdn.net/hegsns/article/details/104857277

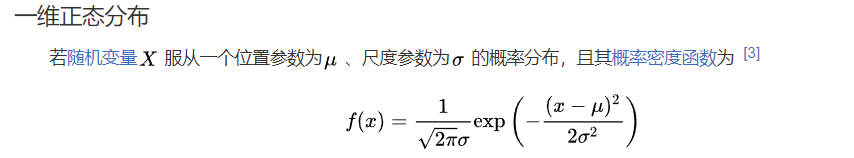
image.png

与Diffusion model有关的工作：

  1. Ho,(2020),Denoising diffusion peobabilistic models
  2. Sohi,(2015), Deep unsupervised learning using nonequilibruim thermodynamics

两篇引入作，尤其是2020的工作，引用上百

扩散模型是受非平衡热力学的启发。它们定义一个扩散步骤的马尔可夫链，逐渐向数据添加随机噪声，然后学习逆扩散过程，从噪声中构建所需的数据样本。
现有的生成模型可以根据如何表示概率分布分为以下两类：

  1. 基于似然的模型，通过（近似）最大似然直接学习分布的概率密度（或质量）函数。典型的基于似然的模型包括自回归模型，归一化流模型, 基于能量的模型 (EBM)和变分自动编码器 (VAE)。
  2. 隐式生成模型，其概率分布由其采样过程的模型隐式表示。最突出的例子是生成对抗网络（GAN），其中来自数据分布的新样本是通过用神经网络转换随机高斯向量来合成的。

然而，基于似然的模型和隐性生成模型都有很大的局限性。基于似然的模型要么需要对模型结构进行严格的限制，以确保似然计算有一个可操作的归一化常数，要么必须依靠代理目标（surrogate objectives）来接近最大似然训练。另一方面，隐式生成模型往往需要对抗性训练，这是众所周知的不稳定，可能导致模式崩溃.

其关键思想是对对数概率密度函数的梯度进行建模，这个量通常被称为（Stein）score function。

一些基于扩散的生成模型被提出，其下有类似的想法，包括扩散概率模型（diffusion probabilistic modelsSohl-Dickstein et al., 2015），噪声条件得分网络（NCSNYang & Ermon, 2019），以及去噪扩散概率模型（DDPMHo et al. 2020）。

image.png