概念理解：

熵（entropy）指的是体系的混乱的程度；
我这里图像熵应该是属于一种信息熵；
信息熵：信息熵简单来说就是把信息进行了量化。通过熵的大小表示信息的混乱程度。一般情况下，图像中包涵的信息量多，熵值越大。

代码实现：

计算一维向量的信息熵：

  1. def entropy(signal):
  2.     '''
  3.     function returns entropy of a signal
  4.     signal must be a 1-D numpy array
  5.     '''
  6.     lensig = signal.size
  7.     symset = list(set(signal))
  8.     numsym = len(symset)
  9.     propab = [np.size(signal[signal == i]) / (1.0 * lensig) for i in symset]
  10.     ent = np.sum([p * np.log2(1.0 / p) for p in propab])
  11.     return ent

读取图片并转变为灰度图（ 建议图片不要太大，不然会运行很久，调整为256左右大小比较好）：

  1. colorIm=Image.open('mo.JPG')
  2. greyIm=colorIm.convert('L')
  3. colorIm=np.array(colorIm)
  4. greyIm=np.array(greyIm)

参数N表示计算熵的区域的大小。
对于N=5，区域包含10*10=100像素值。
在下面的循环中，对每个像素位置提取对应的邻域。
二维的邻域被扁平化为一维的numpy数组并传递给熵函数。
熵值被插入到熵阵E中。

  1. N = 5
  2. S = greyIm.shape
  3. E = np.array(greyIm)
  4. for row in range(S[0]):
  5.     for col in range(S[1]):
  6.         Lx = np.max([0, col - N])
  7.         Ux = np.min([S[1], col + N])
  8.         Ly = np.max([0, row - N])
  9.         Uy = np.min([S[0], row + N])
  10.         region = greyIm[Ly:Uy, Lx:Ux].flatten()
  11.         E[row, col] = entropy(region)

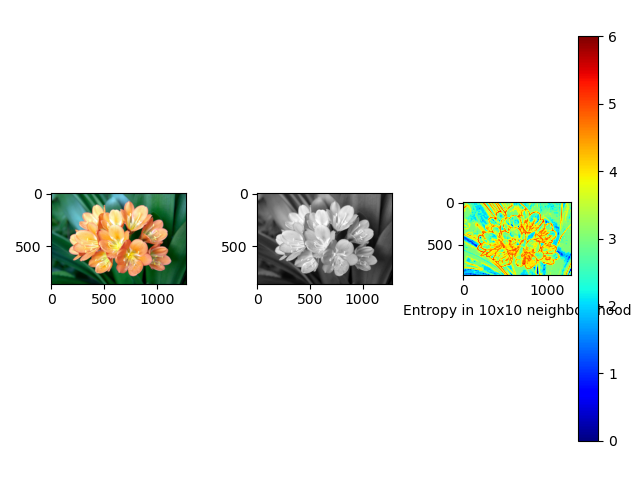
效果展示:

最后利用matplotlib的pyplot函数绘制出原始的RGB图像、对应的灰度图像和熵图像

  1. plt.subplot(1, 3, 1)
  2. plt.imshow(colorIm)
  4. plt.subplot(1, 3, 2)
  5. plt.imshow(greyIm, cmap=plt.cm.gray)
  7. plt.subplot(1, 3, 3)
  8. plt.imshow(E, cmap=plt.cm.jet)
  9. plt.xlabel('Entropy in 10x10 neighbourhood')
  10. plt.colorbar()
  11. plt.show()

image.png

计算图像整体的信息熵

  1. def get_entropy(img):
  2. #输入img 灰度矩阵
  3. #输出图像整体的信息熵
  4.     tmp = []
  5.     val = 0
  6.     k = 0
  7.     res = 0
  8.     for i in range(256):
  9.         tmp.append(0)
  10.     for i in range(len(img)):
  11.         for j in range(len(img[i])):
  12.             val = img[i][j]
  13.             tmp[val] = float(tmp[val] + 1)
  14.             k =  float(k + 1)
  15.     for i in range(len(tmp)):
  16.         tmp[i] = float(tmp[i] / k)
  17.     for i in range(len(tmp)):
  18.         if(tmp[i] == 0):
  19.             res = res
  20.         else:
  21.             res = float(res - tmp[i] * (math.log(tmp[i]) / math.log(2.0)))
  22.     return res