题目描述

  1. 剑指 Offer 16. 数值的整数次方
  2. 实现 pow(x, n) ，即计算 x 的 n 次幂函数（即，xn）。不得使用库函数，同时不需要考虑大数问题。
  6. 示例 1：
  7.     输入：x = 2.00000, n = 10
  8.     输出：1024.00000
  10. 示例 2：
  12.     输入：x = 2.10000, n = 3
  13.     输出：9.26100
  15. 示例 3：
  17.     输入：x = 2.00000, n = -2
  18.     输出：0.25000
  19.     解释：2-2 = 1/22 = 1/4 = 0.25
  22.     提示：
  24.     -100.0 < x < 100.0
  25.     -2^31 <= n <= 2^31-1
  26.     -104 <= x^n <= 104

解题分析

实现幂运算，其实最直接的思路就直接连着乘

  1.     ans = x;   
  2.     while(i<n){
  3.             i++;
  4.             ans = ans*x; 
  5.         }

但是这样显然会有一个问题：注意看题目下方的提示 -2^31 <= n <= 2^31-1
那么当n可能是一个非常大的数字时，采用O(n) 时间复杂度的算法必然会很大
那么有没有更优化的解决方法呢？
就，比如说我 n 这里给的很大，例如 2^64 , 那么我们其实可以发现，这个求解的过程中有很多值我们没有利用起来，2^64 = 2^32 2^32 ; 2^32 = 2^16 2^16 ……. 2^2 = 2*2 那么就可以以一种树状的递归求解方式来求得我们的答案，这种类似树状空间的复杂度为O(logn)级别。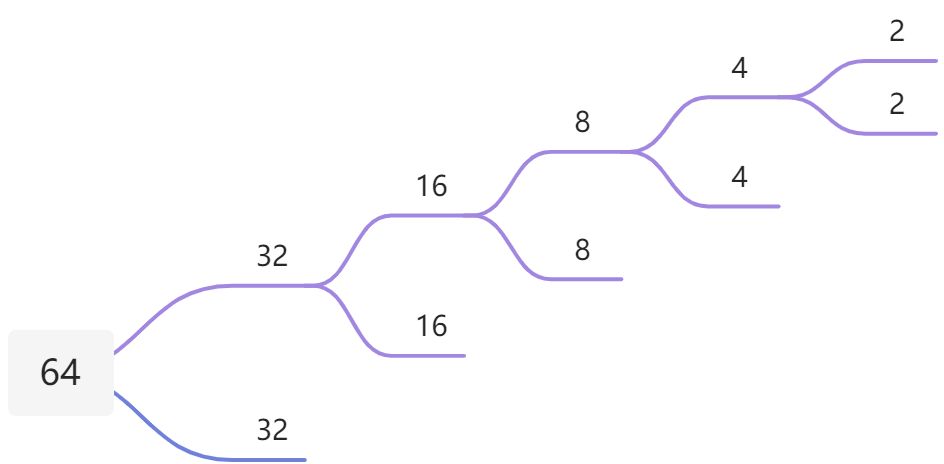
剑指 Offer 16. 数值的整数次方 - 图1
但是这是一种理想的情况，每次都能很好的划分，然后重复利用，那么遇到一个不那么特殊的数怎么办呢？

假设当前数字为 63 ，对吧，你现在一开始就不能直接除二，
那我可以这样：63 = 31+31+1 对吧，就找个比我小但是能二分的数字，然后再乘上一个或者若干个x

那么这种算法的思想其实可以概括为分治法，那么如何具体将这个算法思想转变为代码呢？
lets try! 首先尝试一下递归解法
见3.2
ok,尝试成功，然后去学习一下最优解
由于递归需要使用额外的栈空间，我们试着将递归转写为迭代。
image.png
参考来源：https://leetcode.cn/problems/shu-zhi-de-zheng-shu-ci-fang-lcof/solution/shu-zhi-de-zheng-shu-ci-fang-by-leetcode-yoqr/

其实就是二进制表示的思想，一个数字转化为二进制后的位数上的1 就可以表示这个数字是如何由2的各个多次幂叠加得到，这也就提供了一种拆分计算的快速指示。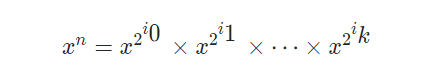
image.png
可以快速的根据n的二进制数上的1来看出，由低到高，哪个等级的x^(2^k)贡献了，需要我们去乘起来

代码实现

笨方法，直接循环

  1. class Solution {
  2. public:
  3.     double myPow(double x, int n) {
  4.         double ans = x;
  5.         int i=1;
  6.         bool flag = true;
  7.         if(n==0) return 1;
  8.         if(x==1) return 1;
  9.         if(x==0) return 0;
  10.         if(n<0) {
  11.             flag = false;
  12.             n = -n;
  13.         }
  14.         while(i<n){
  15.             i++;
  16.             ans = ans*x; 
  17.         }
  18.         if(flag){
  19.             return ans;
  20.         }else{
  21.             ans = 1/ans;
  22.             return ans;
  23.         }
  24.     }
  25. };

递归+矩阵快速幂

  1. class Solution {
  2. public:
  3.     double myPow(double x, int n) {
  4.         //先写递归终止条件
  5.         bool flag = true;
  6.         if(n==0) return 1;
  7.         else if(n==1) return x;
  8.         else if(n<0){
  9.             flag = false;
  10.             n = -n;
  11.         }
  12.         //再写递归规则
  13.         double ans = x;
  14.         int new_n = n/2;
  15.         int rest = n-2*new_n;
  16.         double tmp_ans = myPow(x, new_n);
  17.         ans = tmp_ans*tmp_ans*myPow(x, rest);
  18.         if(flag)    return ans;
  19.         else return 1/ans;
  20.         //好，目前为止这些处理的情况都是n>0，要是n<0怎么办呢？
  21.     }
  22. };

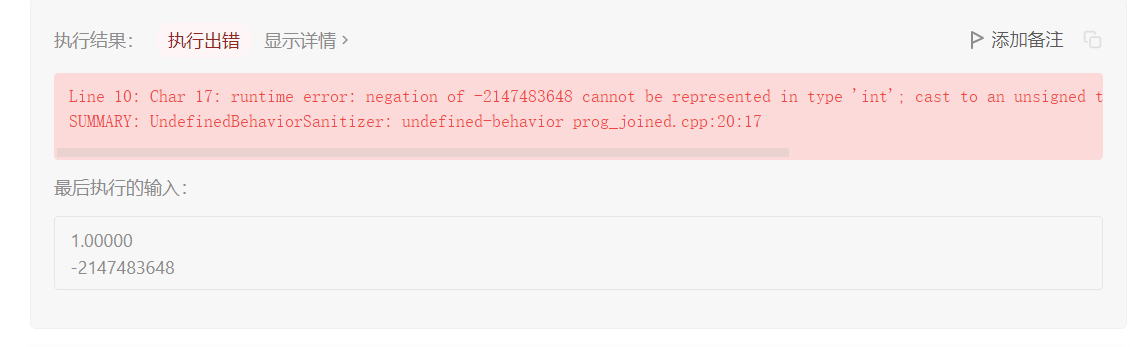
image.png
好吧，有些边界条件要考虑一下：
当 INT_MIN 出现时，n = -n 这个操作会导致 n 变号后直接溢出，那只能特殊处理一下了

  1. class Solution {
  2. public:
  3.     double myPow(double x, int n) {
  4.         //先写递归终止条件
  5.         bool flag = true;
  6.         if(n==0) return 1;
  7.         else if(n==1) return x;
  8.         else if(n<0&&n!=INT_MIN){
  9.             flag = false;
  10.             n = -n;
  11.         }else if(n==INT_MIN){
  12.             n = INT_MAX;
  13.             double ans = x;
  14.             int new_n = n/2;
  15.             int rest = n-2*new_n+1;
  16.             double tmp_ans = myPow(x, new_n);
  17.             ans = tmp_ans*tmp_ans*myPow(x, rest);
  18.             return 1/ans;
  19.         }
  20.         //再写递归规则
  21.         double ans = x;
  22.         int new_n = n/2;
  23.         int rest = n-2*new_n;
  24.         double tmp_ans = myPow(x, new_n);
  25.         ans = tmp_ans*tmp_ans*myPow(x, rest);
  26.         if(flag)    return ans;
  27.         else return 1/ans;
  28.     }
  29. };

image.png

官方最快方法(迭代+矩阵快速幂)

  1. class Solution {
  2. public:
  3.     double quickMul(double x, long long N) {
  4.         double ans = 1.0;
  5.         // 贡献的初始值为 x
  6.         double x_contribute = x;
  7.         // 在对 N 进行二进制拆分的同时计算答案
  8.         while (N > 0) {
  9.             if (N % 2 == 1) {
  10.                 // 如果 N 二进制表示的最低位为 1，那么需要计入贡献
  11.                 ans *= x_contribute;
  12.             }
  13.             // 将贡献不断地平方
  14.             x_contribute *= x_contribute;
  15.             // 舍弃 N 二进制表示的最低位，这样我们每次只要判断最低位即可
  16.             N /= 2;
  17.         }
  18.         return ans;
  19.     }
  21.     double myPow(double x, int n) {
  22.         long long N = n;
  23.         return N >= 0 ? quickMul(x, N) : 1.0 / quickMul(x, -N);
  24.     }
  25. };