题目描述

  1. 给你一个字符串 s，找到 s 中最长的回文子串。
  5. 示例 1：
  7. 输入：s = "babad"
  8. 输出："bab"
  9. 解释："aba" 同样是符合题意的答案。
  10. 示例 2：
  12. 输入：s = "cbbd"
  13. 输出："bb"
  16. 提示：
  18. 1 <= s.length <= 1000
  19. s 仅由数字和英文字母组成
  21. 来源：力扣（LeetCode）
  22. 链接：https://leetcode.cn/problems/longest-palindromic-substring
  23. 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

题目分析

思路一：中心扩散法 O(n^2)

对于字符串中的每一个字母，我们可以按照两种规则来判断是否存在回文串，同时来判断长度

第一种情况：奇数个

以该字母为中心，采用两个下标x，y来移动，x每次-1直到减小为0，y每次+1直到增加为length - 1
每次移动后判断：x,y下标对应的字符是否相同，如果相同的话，那说明以该字母为中心的回文长度+2
如果不同的话，那说明判断结束，记录当前长度L，ans = max(L)

第二种情况：偶数个

以该字母和该字母右边的字母为中心（如果有，而且这两个字母相同的话开始，否则为0）
x y两个坐标开始更新,如果相同的话，那说明以该字母为中心的回文长度+2
如果不同的话，那说明判断结束，记录当前长度L，ans = max(L)
时间复杂度： O(n*n)
可以优化的点：可以先从中间位置开始搜索每个字母，如果出现当前的max/2 > i 或者 max/2 < len-i 的话说明已经找到最大的了，可以减少搜索次数

思路二： Manacher 算法O(n)

这个算法不是我想出来的，参考官方题解才得知，所以这里先不实现
只先学习理解
确实在中心扩散法的算法中，有信息被浪费了，没有充分利用，我们可不可以在一次遍历的过程中，去帮助其他位置进行判断？或者换种想法，我们在判断当前某一位置的过程中，能不能利用之前遍历过的信息，快速的得到结论呢？

那么我们看一下这种算法是怎么利用好遍历过程中的信息的

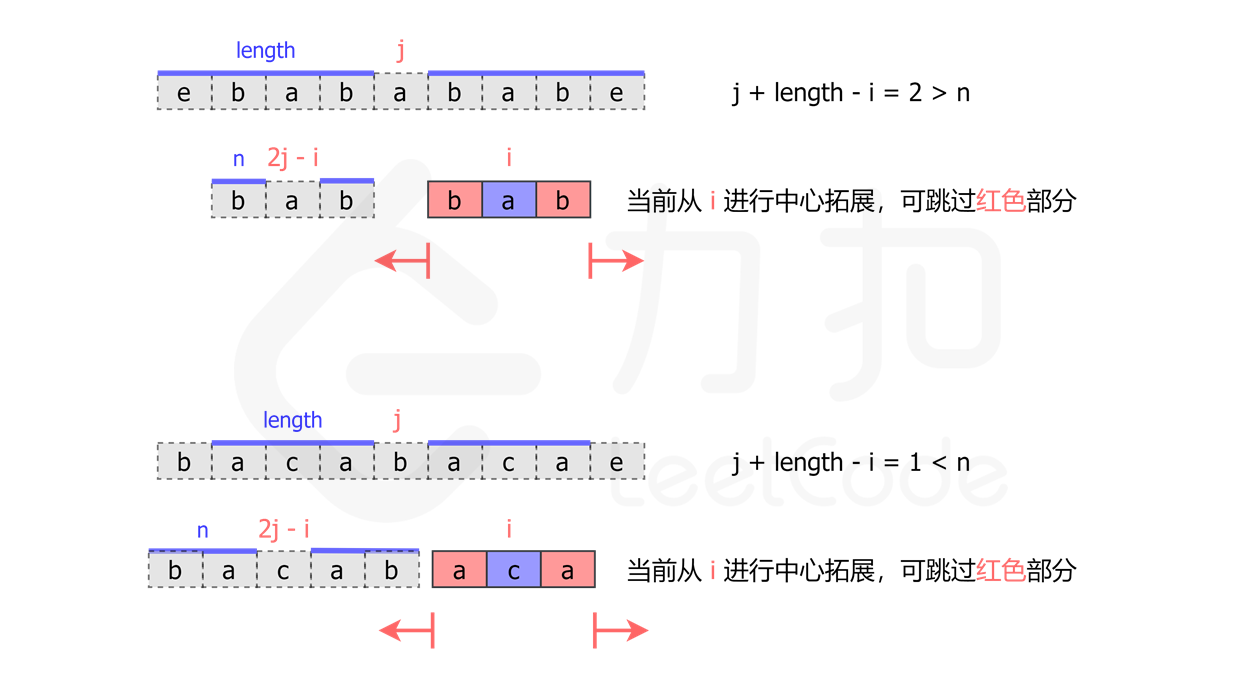
image.png

当在位置 i 开始进行中心拓展时，我们可以先找到 i 关于 j 的对称点 2 j - i。那么如果点 2 j - i 的臂长等于 n，我们就可以知道，点 i 的臂长至少为 min(j + length - i, n)。那么我们就可以直接跳过 i 到 i + min(j + length - i, n) 这部分，从 i + min(j + length - i, n) + 1 开始拓展。

光靠这个讲解没看懂。。。。所以算作一个坑吧，以后来看

思路三：DP+信息利用O(n)

这个问题有最优子结构，我可以用一个DP数组来记录当前以位置为最右端的最长回文串的长度，
baaaab
我可以用Dp1 Dp2两个动归数组来，DP1全部初始化为1，DP2全部初始化为0
DP1用于维护以当前数字为最右端的奇数最长回文串长度，1+2+2…
DP2用于维护以当前数字为最右端的偶数最长回文串长度，0+2+2+…
每次检索到一个新的位置，就用这个位置和DP1和DP2中前一位置最长回文串另外一头的元素去对比，这个找到对应位置只用O(1)，而遍历需要O(n)，所以综合下来是O(n)

代码实现

  1. class Solution {
  2. public:
  3.     string longestPalindrome(string s) {
  4.         int len = s.length();
  5.         int max = 1;
  6.         int max_start = 0;
  7.         if(len==1) return s;
  8.         vector<int> dp1(len,1);
  9.         vector<int> dp2(len,0);
  10.         for(int i=1;i<len;i++){
  11.             //dp1
  12.             int k = i-1-dp1[i-1];
  13.             if(k>=0){
  14.                 if(s[k]==s[i]){
  15.                     dp1[i]=dp1[i-1]+2;
  16.                     if(dp1[i]>max){
  17.                         max = dp1[i];
  18.                         max_start = i-max+1;
  19.                     }
  20.                 }
  21.             }else if(dp2[i-1]){
  22.                 dp1[i-1]-=2;
  23.             }
  25.             //dp2
  26.             k = i-1-dp2[i-1];
  27.             if(k>=0){
  28.                 if(s[k]==s[i]){
  29.                     dp2[i]=dp2[i-1]+2;
  30.                     if(dp2[i]>max){
  31.                         max = dp2[i];
  32.                         max_start = i-max+1;
  33.                     }
  34.                 }
  35.                 else if(s[i]==s[i-1])   dp2[i]=2;
  37.             }else if(s[i]==s[i-1])   dp2[i]=2;
  38.         }
  39.         return s.substr(max_start, max);
  41.     }
  42. };