Kmeans聚类算法 - 《sklearn》

概念：聚类算法又叫做“无监督分类”，是聚类算法中最简单的一种，其目的是将数据划分成有意义或有用的组（或簇）。聚类算法虽然强大，但是它有一个很大的缺点：时间复杂度十分之大。
使用情景：比如在商业中，如果我们手头有大量的当前和潜在客户的信息，我们可以使用聚类将客户划分为若干组，以便进一步分析和开展营销活动，最有名的客户价值判断模型RFM，就常常和聚类分析共同使用。
簇与质心：

在Kmeans中，超参数就为想要分成的簇数K

Kmeans是如何迭代的：

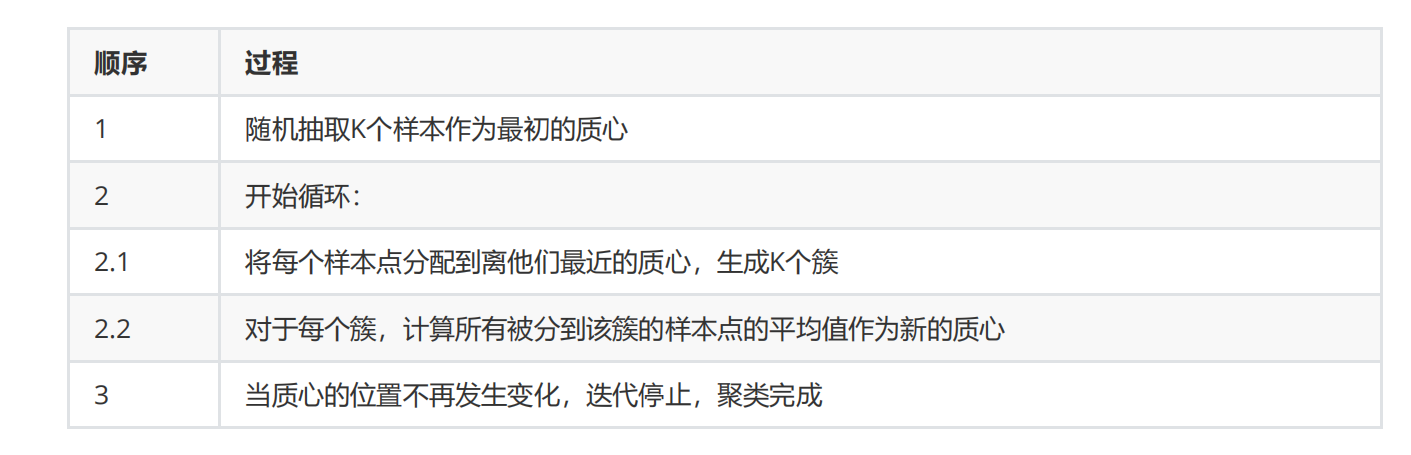
图解：

个人理解：给出一个需要分类的图像，输入要分出的簇数K，然后Kmeans会在图像中先随机生成K个质心，然后计算每个点到四个质心的距离，进行初步分类，分类完重新再从K个簇中取质心，再继续进行进一步划分，重新生成K个簇，再继续从K个簇中找出新的质心，反复迭代，直到质心不再变化。

簇内误差平方和

聚类算法追求“簇内差异小，簇外差异大”。而这个“差异”，由样本点到其所在簇的质心的距离来衡量。而簇内误差平方和就是这个距离的衡量指标（有点类似于数学中的两点距离），该样本点
到质心的距离可以由以下距离来度量**
x表示簇中的一个样本点，u 表示该簇中的质心，n表示每个样本点中的特征数目，i表示组
成点的每个特征，假如我们采用欧几里得距离，则一个簇中所有样本点到质心的距离的平方和为：

这个公式被称为簇内平方和（cluster Sum of Square），而将一个数据集中的所有簇的簇内平方和相加，就得到了整体平方和（Total Cluster Sum of Square），又叫做total inertia。Total Inertia越小，代表着每个簇内样本越相似，聚类的效果就越好。因此 KMeans追求的是，求解能够让Inertia最小化的质心。来到最值问题的时候，我们第一时间就会想到我们的最优化问题了。

提到最优化问题，肯定就是我们的梯度下降了，某种意义上，我们可以把簇内平方和/整体平方和看成是KMeans的损失函数。（不严谨，详细见文末），值得一提的是，在sklearn当中，我们无法选择使用的距离，只能使用欧式距离。而且就像开头说的，簇类算法时间复杂度十分大，因为要计算每一个点到质心的欧式距离，并且不断迭代。

轮廓系数先抛出一个问题：
有说会立刻就说，Inertia最小化，但实际并不完全是这样子的，首先Kmeans聚类算法是无监督学习算法，我们要根据实际问题实际分析，其次如果数据特征太多，一次次的计算最小Inertia会使计算量爆炸，所以我们就引进了一个新的参数：轮廓系数，它可以评价簇内的稠密程度（簇内差异小）和簇间的离散程度（簇外差异大）来评估聚类的效果，具体为：**

s 越接近于1越好，越接近于-1越差，0表明表两个簇中的样本相似度一致，两个簇本应该是一个簇。

但轮廓系数也有缺陷，它在凸型的类上表现会虚高，比如基于密度进行的聚类，或通过DBSCAN获得的聚类结果，如果使用轮廓系数来衡量，则会表现出比真实聚类效果更高的分数。

在sklearn中，我们使用模块metrics中的类silhouette_score来计算轮廓系数，它返回的是一个数据集中，所有样本的轮廓系数的均值。但我们还有同在metrics模块中的silhouette_sample，它的参数与轮廓系数一致，但返回的是数据集中每个样本自己的轮廓系数。

from sklearn.metrics import silhouette_score
from sklearn.metrics import silhouette_samples
silhouette_score(X,y_pred)
silhouette_samples(X,y_pred)

calinski-Harabaz指数
与轮廓系数相比，还有一个我更喜欢的参数，有卡林斯基-哈拉巴斯指数（Calinski-Harabaz Index，简称CHI，也被称为方差比标准），因为它比轮廓系数的运行速度快很多。

calinski-Harabaz指数没有界，在凸型的数据上的聚类也会表现虚高。

from sklearn.metrics import calinski_harabaz_score
calinski_harabaz_score(X, y_pred)

**重要参数

n_clusters：超参数，簇数k