最近在深入接触区块链后，发现有太多密码学知识没有了解过，特整理一些文章补补课。

    椭圆加密算法（英语：Elliptic curve cryptography，缩写为ECC）是一种公钥加密体制，最初由 Koblitz 和 Miller 两人于1985年提出，其数学基础是利用椭圆曲线上的有理点构成 Abel 加法群上椭圆离散对数的计算困难性。

    ECC 是一种目前非常场景的加密算法，最著名的 TLS（传输层安全协议）就是用了 ECC 作为其加密算法部分；包括大部分加密货币（包括比特币）都借助 ECC 来实现其密码学证明部分。

    相比于 RSA（另一种更加常用的非对称加密算法，用于很多场景比如 ssh 等），ECC 越来越趋于主流，能够用更短的密钥长度（ECC 256 位、RSA 2048 位）来获得更高的性能、更高的效率和更强的抗攻击性。

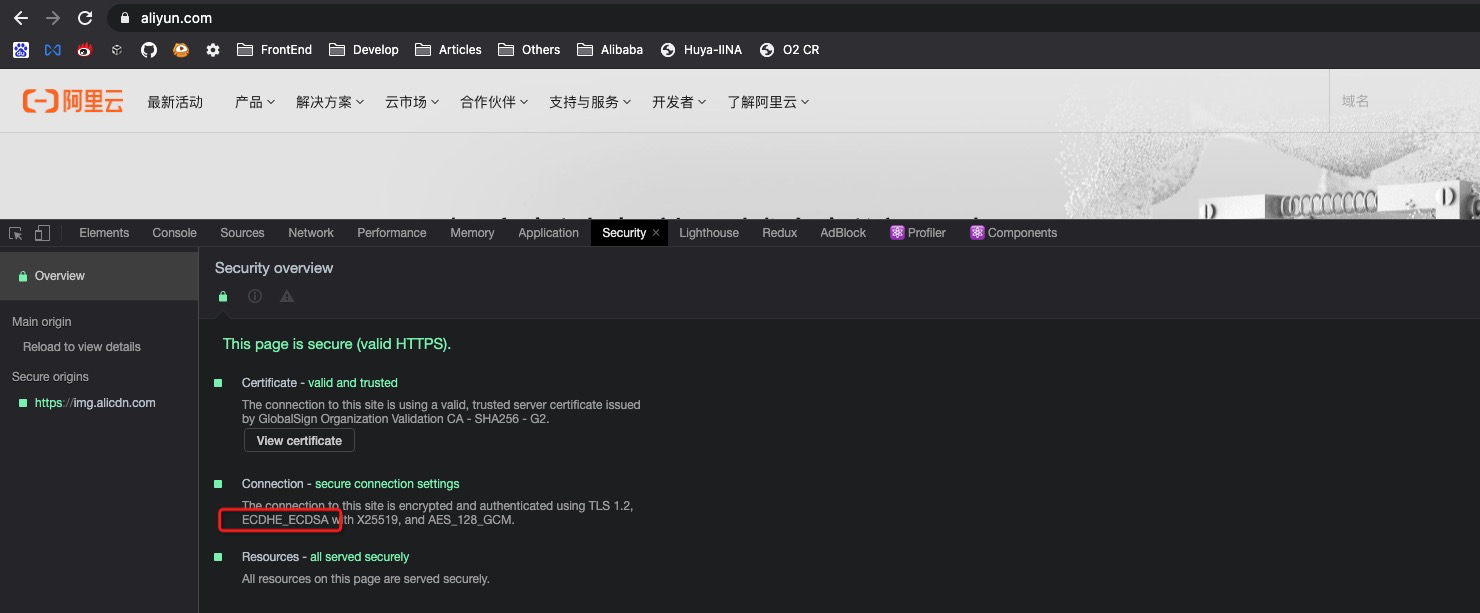
    image.png
    阿里云官网 TLS 证书可以看到用了 ECC 加密算法

    公钥加密体制（Public-key cryptography）：与「公开密钥密码体系」、「非对称加密（Asymmetric cryptography）」在密码学上是同一个概念。

    它由公钥和私钥组成，公钥用来将明文加密，私钥用来将密文解密。相比于「对称加密」的只有一个密钥，加解密都是用相同的一个密钥，这就存在「如何将密钥在两方之间安全的传输」的问题，而「非对称加密」可以很好的解决这个问题（公钥可以安全的对外透出）。

    在加密/数字签名场景，如何区分什么时候要用公钥，什么时候要用私钥？ 加密场景：既然是加密，那一定不希望别人能够解密我的内容，所以只有我自己（私钥）才可以解密； 签名场景：签名一定是希望只有我才能发出签名，别人无法模仿，只能验证，所以要用私钥签名，公钥验证；

    群（Group）是一个类似于「集合」的数学概念，但比「集合」的概念要前沿不少，也可以简单理解为一种特殊的集合：椭圆加密算法（ECC） - 图2，群内一种与次序有关的二元运算我们定义为「群乘」。

    群一般满足如下四个条件：
    1、封闭性（群内任意两元素的群乘后得到的元素还在这个群中） 椭圆加密算法（ECC） - 图3
    2、结合律（群乘必须满足结合律） 椭圆加密算法（ECC） - 图4
    3、群中存在单位元（元素 0） 椭圆加密算法（ECC） - 图5
    4、逆元（元素 -n，群中存在任一元素的逆元） 椭圆加密算法（ECC） - 图6

    有理点指的是在「数轴」上表示有理数（正整数、负整数、正分数、负分数以及零的统称）的点，同样的在一个多维坐标系中，一个点的坐标可以用 椭圆加密算法（ECC） - 图7 来表示，如果坐标都是有理数，那么这个点也是有理点。

    结合椭圆曲线的定义，可以很好的理解什么是「椭圆曲线上的有理点」。

    Abel 加法群：我们一般称为「阿贝尔群」或者是「可交换群」：

    • 通俗的讲，满足「交换律」的群就是「Abel 群」 椭圆加密算法（ECC） - 图8
    • 群内定义的运算为「加法」的群为「加法群」
    • 综上可解释什么是 Abel 加法群

    「加法」和「乘法」是 Abel 群上最主要的两种运算方式：

    约定 运算 单位元 幂 逆元
    加法运算 x+y 0 nx −x
    乘法运算 x*y或xy e或1 x^n x^-1

    椭圆曲线在数学上定义比较宽泛，基本可以认为符合如下方程定义的平面代数曲线就是椭圆曲线：
    椭圆加密算法（ECC） - 图9

    虽然叫做「椭圆曲线」，但图像和「椭圆」不沾边，主要是因为其曲线方程跟利用微积分计算椭圆周长的共识相似。他们一般有下面两个特点：

    1. 关于 x 轴对称
    2. 直线与椭圆曲线的交点最多有 3 个

    下图是公式 椭圆加密算法（ECC） - 图10对应的曲线：

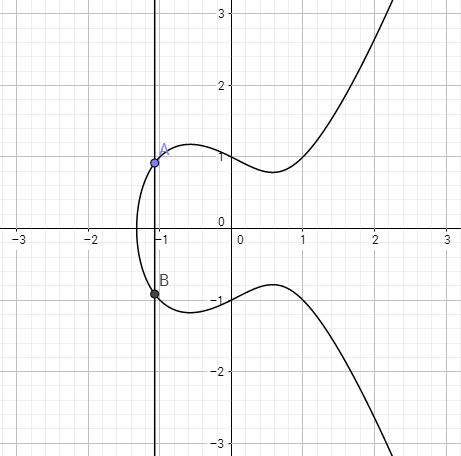
    image.png

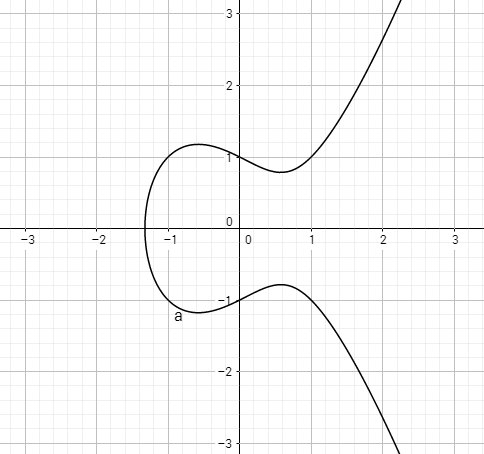
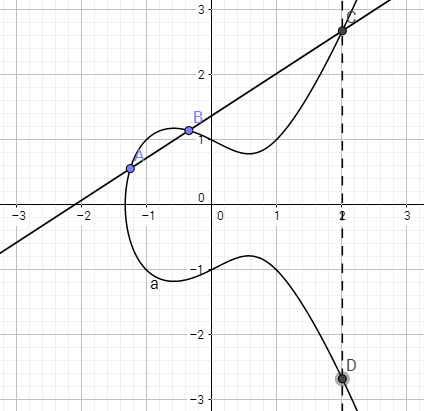
    我们定义在「椭圆曲线上有理点」的「加法」运算：假设曲线上两个点 A 和 B，所确定的直线与曲线相交于第三点 C，C 关于 x 轴对称的点为 D。我们定义 D 为 A 与 B 的加法运算结果，记作 椭圆加密算法（ECC） - 图12
    可以看到两个点做「加法」运算的结果点一定还在「椭圆曲线」上，这也就满足我们上面说过的「群的封闭性」。

    image.png

    当两点重合时，我们使用这个曲线在 A 点的切线，与曲线相交与第二点 B，B 关于 x 轴对称的点为 C。根据上面的结论可以得出：椭圆加密算法（ECC） - 图14

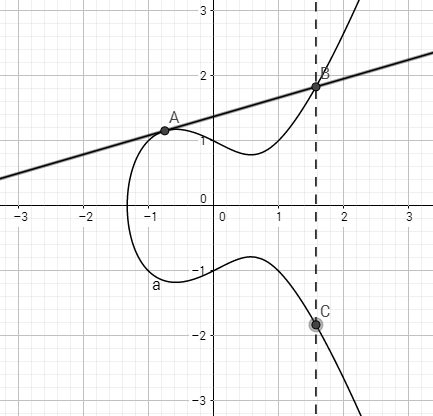
    image.png

    结合上面两个图，我们可以分析出两个结论：

    1. 曲线上的点满足「Abel 群的交换律」椭圆加密算法（ECC） - 图16 。两点确定的直线没有方向，很简单可以理解
    2. 满足「群的结合律」椭圆加密算法（ECC） - 图17 我花了些时间做了下图，可以验证。官方验证可以参考这篇论文：http://www.andrew.cmu.edu/user/tnayak/papers/EllipticCurves.pdf

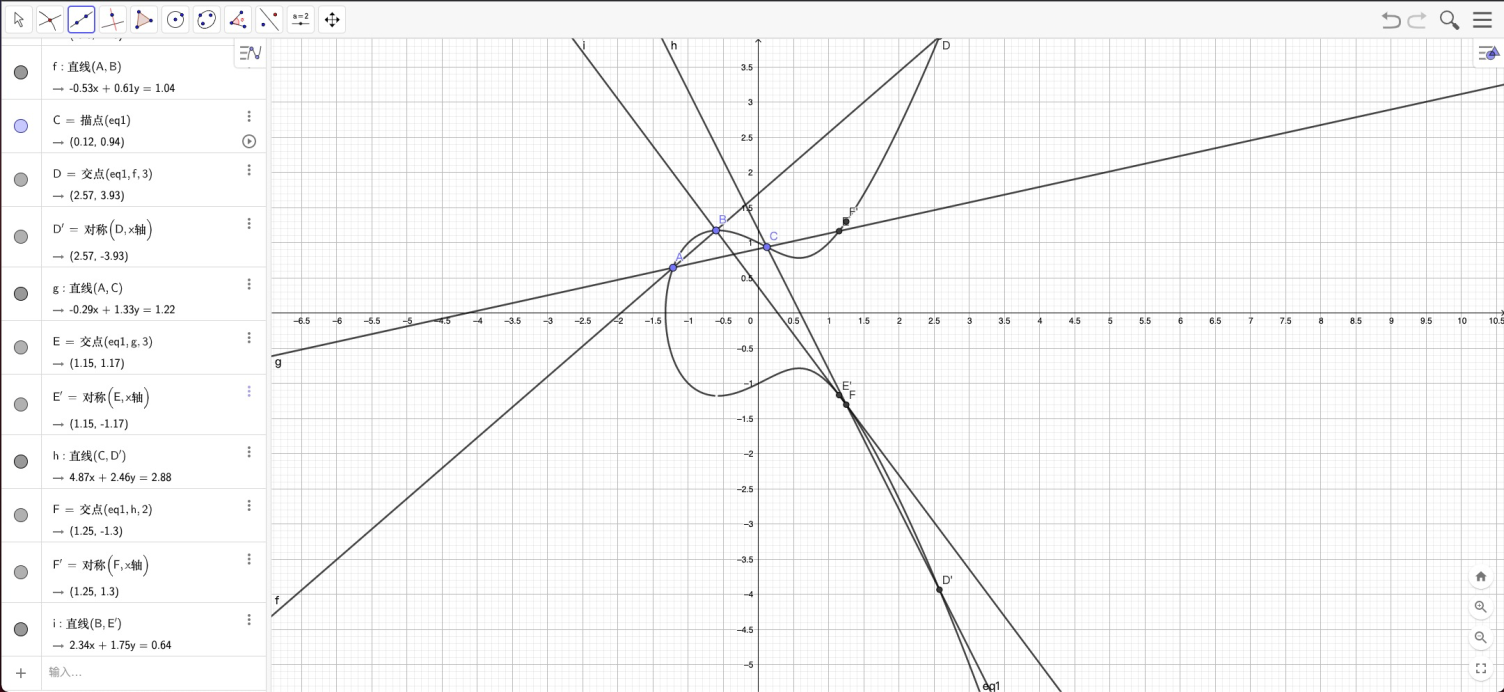
    image.png
    当两个点 A、B 所形成的曲线与 x 轴恰好垂直时，两点形成的直线与椭圆曲线只能有两个交点，所以我们定义距离 x 轴无穷远的点也在椭圆曲线上，任意与 x 轴垂直的线都经过这个点，这个特殊点我们称为「零点」。紧接着可以得出以下几个结论：

    1. 对于椭圆曲线上任意一点 A，都存在一点 B 使得 椭圆加密算法（ECC） - 图19 （满足群上的单位元特性）
    2. 符合群上的逆元特性：椭圆加密算法（ECC） - 图20
    3. 椭圆曲线中的「负数」：椭圆加密算法（ECC） - 图21

    image.png

    经过验证，我们重新定义的在椭圆曲线上的 0、加法、减法 完全可以构成新的「加法运算体系」，同时也支持交换律和结合律。

    下面我们尝试理解「椭圆曲线上的乘法」，它与常见乘法的推导一致，假定正整数 n 乘椭圆曲线上的点 A：

    • 椭圆加密算法（ECC） - 图23
    • 椭圆加密算法（ECC） - 图24
    • 椭圆加密算法（ECC） - 图25
    • 椭圆加密算法（ECC） - 图26
    • 椭圆加密算法（ECC） - 图27

    再从程序实现上来看，我们定义一个函数用来实现椭圆曲线上的加法（只是定义）：

    1. /**
    2.  * add 定义了椭圆曲线上的加法
    3.  * 返回值为加法结果的点
    4.  */
    5. function add(A: Point, B: Point): Point;

    那么可以用这个方法实现椭圆曲线上的乘法：

    1. /**
    2.  * add 实现了椭圆曲线上的乘法
    3.  * 返回值为乘法结果的点
    4.  */
    5. function multip(n: number, A: Point): Point {
    6.     let result: Point;
    7.   for (let i = 0; i < n - 1; i += 1) {
    8.       result = add(result, A);
    9.   }
    10.   return result;
    11. }

    对于任意正整数 m、n，可以证明在椭圆曲线上的点乘公式：椭圆加密算法（ECC） - 图28 ，所以使用「快速幂算法」可以显著减少加法运算次数，这也是 ECC 比 RSA 要更高效的原因之一。

    什么是快速幂算法：

    • 椭圆加密算法（ECC） - 图29
    • 椭圆加密算法（ECC） - 图30
    • 椭圆加密算法（ECC） - 图31
    • 椭圆加密算法（ECC） - 图32 注意这里计算 23P 只进行了 7 次加法

    可以看到，使用这种方法计算 椭圆加密算法（ECC） - 图33 时，随着 n 变大时间复杂度是对数级的，但知道 椭圆加密算法（ECC） - 图34 和 椭圆加密算法（ECC） - 图35 反过来推导 n 的值是非常难的，基本上除了「暴力尝试」外没有更好的算法。
    这也就是文章一开始所提到的「椭圆曲线离散对数计算困难性」。

    但我们在尝试理解「椭圆曲线加密算法」时，要将数域限定到「有理数域」。

    引用：