前情提要
线性回归模型解决的预测值是连续值
分类问题的预测值是离散的
让人工智能学习分类是一个复杂的过程，需要优秀的模型、海量的数据和高性能的硬件支持
逻辑斯蒂分类
通过拟合线性函数进行回归分类，为了实现二分类，理想情况是一个单位阶跃函数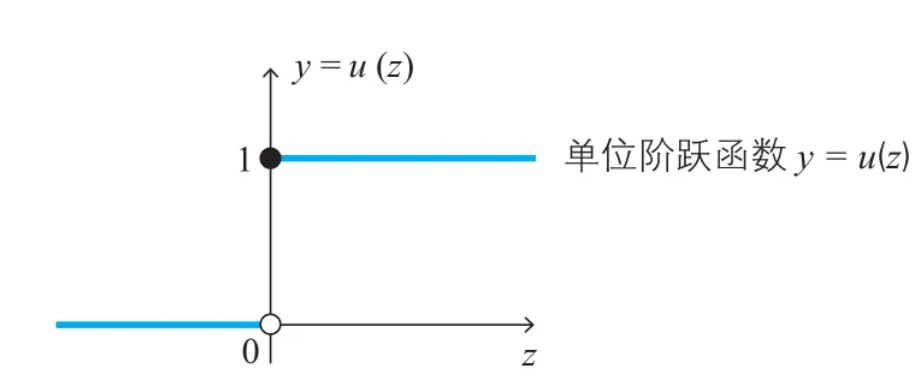
逻辑斯蒂函数的形式如图：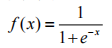
f(x)取值在0~1之间，x无限大时，y趋近于1，x无限小时，y趋近于0
虽然逻辑斯蒂函数是连续的，但却有二分类的特点
对于二分类问题，两个类分别用0和1表示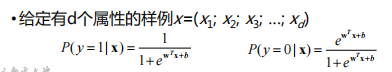
二分类逻辑斯蒂分类问题提出与分析
当逻辑斯蒂分类类别数量只有两个时（即y的取值
是0或1），是二分类逻辑斯蒂分类模型
目标是要找到一个最好的边界把两类分开
比如二维角度如果是可分的，可以找到一条斜线，把所有样本无交叉地分割在直线两端，同时保证这条线不是曲线，还是线性组合关系，wx+b
基于sklearn库求解双类别逻辑斯蒂分类
使用Scikit-learn库的LogisticRegression类解决逻辑斯蒂分类问题
from sklearn.linear_model import LogisiticRegressionmodel=LogisticRegression(penalty='l2', dual=False, tol=0.0001, C=1.0, ``fit_intercept=True, intercept_scaling=1, ``class_weight=None, ``random_state=None, solver='liblinear', max_iter=100, ``multi_class='ovr', verbose=0, warm_start=False, n_jobs=1)
主要参数：
• penalty：正则化参数，可选值为“L1”和“L2” • solver：优化算法选择参数 • liblinear：使用坐标轴下降法来迭代优化损失函数 • lbfgs：拟牛顿法的一种 • newton-cg：也是牛顿法家族的一种 • sag：随机平均梯度下降 • multi_class：分类方式选择参数 • class_weight：类别权重参数 • fit_intercept：是否存在截距 • max_iter：算法收敛的最大迭代次数
主要属性和方法
- 拟合函数fit ( X, y )通过训练数据x和训练数据标签y来拟合模型
- 预测函数predict ( X )通过拟合好的模型，对数据x预测y值
- 预测概率函数predict_proba(X),
- 评价分数值score ( X, y )
求解步骤
- 准备训练数据
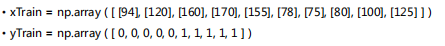
- 创建logisticRegression对象并执行拟合
先导入该类，在创建对象，定义一个优化算法
- 执行拟合
调用模型对象的fit()函数，传入xtrain和ytrain作为参数，进行模型拟合，获得拟合的模型参数
- 对新数据进行预测
梯度下降法
梯度下降法优化目标
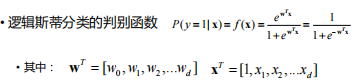
w是一个d+1维的向量，w0其实是截距b x是一个具有d个特征的样本，1和w0对应
训练数据中有m个样本，y(i)=0表示第i个样本的实际类别为第0类，y(i)=1表示该样本的实际类别为第1类。
•M0为实际类别为0的样本子集，M1为实际类别为1的样本子集
两类合并后，优化目标为：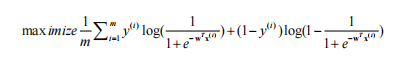
左半部分是用实际类别为1的训练样本进行优化，左半部分是用实际类别为0的训练样本进行优化
优化目标一般是进行最小化而不是最大化，L(w)也被称为损失函数（Loss Function）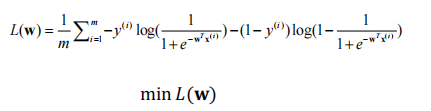
梯度计算
梯度下降法需要根据梯度更新参数
更新公式为：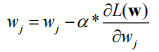
偏导数的求解推导过程：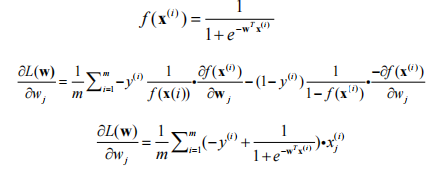
输出结果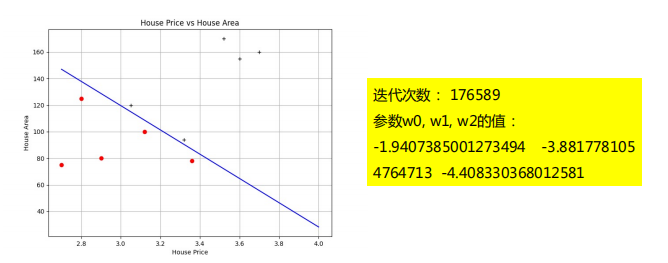
在样本数据传入
梯度下降函数进行训练之前先进行归一化操作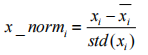
训练数据的两个属性分别对应优化参数w1和w2，由于参数向量也包含w0，而w0与1对应，因此为了便于向量运算，在训练数据属性向量中增加一个值为1的量，对应代码中的make_ext()函数。
整个过程：
- 问题建模
• 回归、分类 … 收集数据
• 回归：特征数据X，连续数据y• 分类：特征数据X，离散数据y
特征预处理
• 归一化
• 类别特征
• 时间特征
• 图像数据、序列数据、图结构数据- 构建模型
• 模型选择：线性回归、Logistic Regression
• 损失函数：均方误差 - 模型验证&参数调优
• 使用训练数据训练模型，使用验证数据进行参数调优
• 验证指标：回归（wmape、R2、均方误差）
模型上线/AB测试
• 在测试数据上进行模型测试（测试数据和训练数据来自于同一分布）
分类模型的评价
几个评价指标：
正确率、准确率、召回率、F1分数、ROC曲线真阳TP，预测结果是1，真实类别也是1的样本的数量，预测正确 假阳FP，预测结果是1，真实类别为0的样本的数量，预测错误 真阴TN，预测结果是0，真实类别也是0的样本的数量，预测正确 假阴FN，预测结果是0，真实类别是1的样本的数量，预测错误
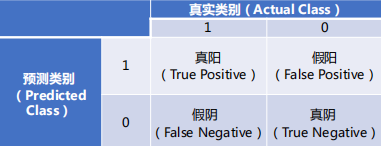
正确率反映了争取的样本数占总样本数的比重
准确率反映了“误报”的程度，准确率越高，误报越小
召回率反映了“漏报”的程度，召回率越高，漏报越小
P是Precision，R是Recall，F1-Score是对准确率和召回率的折中
运行结果说明
测试数据集中共有5个样本，并给出真实y值用于评价；计算预测y值前，先将属性值归一化，再根据分类模型预测y值。
语句“yTest_real_pred = yTestPredicted == yTest”是将预测值与真实值逐项比较，相同则对应的项为1，不相同则对应的项为0，注意正例和负例都进行了比较，此时预测值为[1, 1, 0, 1, 0]，真实值为[1, 0, 1, 1, 1]
逻辑斯蒂分类模型计算出来的是概率值，判定时需设定一个阈值K，当概率值大于等于K时判定为正例，小于K时判定为负例
ROC曲线
接受者操作特性曲线（receiver operating characteristic curve， 简称ROC曲线），也叫感受性曲线
横轴：TPR真阳性率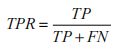
纵轴：FPR假阳性率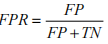
反映模型在选取不同阈值K的时候其真阳性率和假阳性率的趋势走向
理想的情况是：TPR越高越好，FPR越低越好
曲线下的面积被称为AUC （Area under curve）
取值范围为0~1
AUC固定阈值，允许中间状态的存在；有助于选择最佳的阈值。ROC曲线越靠近左上角，模型的准确性就越高
非线性分类问题
更多情况下，样本数据是线性不可分的，通过一个（多个）曲线或曲面才能分割
基于sklearn实现
要使用高阶曲线来区分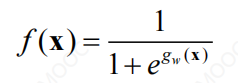
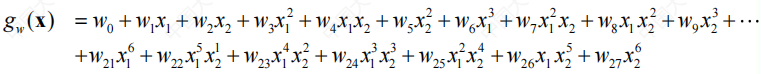
x1和x2是样本的两个属性，进行多种乘方组合变化，可以得到共28组不同的特征
正则化问题
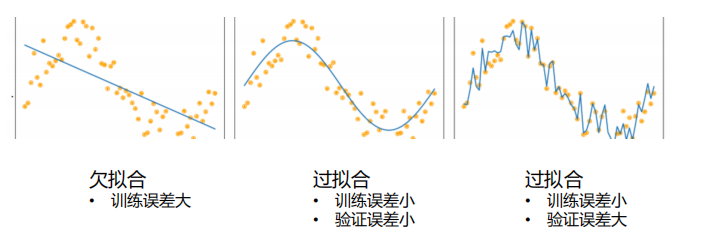
为了防止过拟合问题，正则化方法被提出来了
核心思想是：
由于特征数量维度多而造成权重参数也很多， 应尽可能使每个权重参数的值小， 以降低模型复杂度和不稳定程度， 从而避免过拟合的危险。
奥卡姆剃刀定律（Occam’s Razor）：如果有多个假设与观察一致，则选最简单的那个
采用的方法是在成本函数中加入一个惩罚项。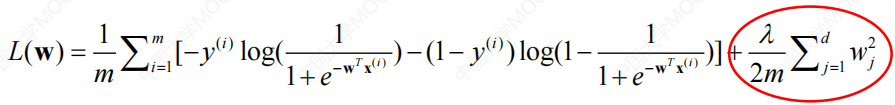
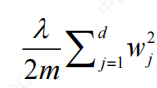是惩罚项，即penalty项，是对参数数量和大小的约束
惩罚项是有范式的，以上是二范式项；
也可以根据需要替换成零范式（要么有参数wj，要么没有参数wj）、一范式、三范式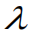
是超参数，用于调整惩罚项的权重
- 惩罚项的梯度是
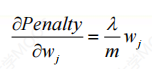
- 得到成本函数的梯度：
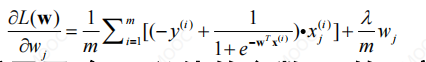
- 该式适用于w0以外的参数wj的更新
正则化问题的求解实现
只需要将其中创建模型对象的语句修改成如下语句即可model = LogisticRegression ( solver = "newton-cg", penalty = “l2" )#可选：l1, l3, l4等 等
由于数据的两个属性值取值范围相同，因此可以省去归一化（normalize）部分关于防止过拟合
过拟合发生的原因：
- 训练数据集样本单一，样本不足
- 训练数据中噪声干扰过大
- 模型过于复杂
常用防止过拟合的方法
使用更多的数据 控制模型复杂度 减少特征的数量 正则化
多类别逻辑斯蒂分类
- 准备训练数据
- 计算特征矩阵用于模型训练
若有收获，就点个赞吧
0 人点赞
