这一篇,我们来谈谈,为什么 MySQL 要用 B+ 树这种结构来存储索引,当然不会去过多的追溯 B+ 树的各种操作,还是以浅谈为主。
1. 能不能用数组或者哈希表
1.1 数组
首先先看看数组,数组属于典型的线性结构,其定义就是在内存中,开辟一块连续的内存空间,定义一个数组对象,创建对象后,就能获取到对应的内存起始地址,所以这种数据结构,在知道下标的前提下,可以非常方便的获取到该下标对应位置的元素,即时间复杂度为 O(1) 。
如果对于一个非下标的元素查询,可以使用二分查找,时间复杂度为 O(logn),因为数组存储是顺序的,所以范围查找等操作也非常友好,而更新删除等,在知道下标的前提下也非常容易。
但是对于插入操作,需要在两个元素之间 ”硬“ 挤进去一个元素,所以后面的元素都需要被迫向后移动,同时如果这个元素越靠前,或者插入位置后面的元素过多,就会导致这个操作越耗时,就从这个观点上看,数组也不合适作为索引的底层数据结构。同时二分查找的前提,整个数据都要事先在内存中,数据大的情况下,几乎不可能。
线性表:具有零个或多个(具有相同性质,属于同一元素的)数据元素的有限序列。
1.2 哈希表
在 Navicat 等可视化软件中,当你编辑表设计的时候,会发现索引其实除了默认的 B+ 树之外,还有 Hash 这种结构,这是怎么说呢?
首先,哈希表其实就是一种 key value 的数据结构,底层采用的是数组和链表,将 key 经过 hash 函数后,计算出下标作为数组的存储位置,如果不同元素计算出的下标一致,则属于哈希冲突,需要在同一位置存储两个元素,这个时候,这个元素的位置就变成了一个链表来依次存储这几个相同位置的元素。
而根据其特性,其实可以看出来,它对于增删改查其实都是非常方便的,因为只需要围绕 key 和 hash 函数,时间复杂度都是 O(1),速度很快。
但是如果我们需要在 MySQL 中查找范围查询,例如大于等于、小于等于,between 等等。就会遇到问题,因为经过 hash 存储后,数据已经变得无需了,范围查询就需要遍历全部的数据,当数据多的时候,这个过程会非常耗时。
所以,如果只有在业务场景确实属于 key value 这种结构的前提下,才可以考虑使用哈希结构,否则还是推荐 B+ 树。
2. 树的选择
下面的配图会大部分使用这个很有名的网站,来模拟各种树。贵在方便和可视化动态演示,图片质量比较一般。
地址:Data Structure Visualizations
2.1 二叉查找树
二叉查找树(Binary Search Tree)又称二叉排序树(Binary Sort Tree),亦称二叉搜索树。是数据结构中的一类。在一般情况下,查询效率比链表结构要高。
对于二叉查找树来说,有一个很重要的结论,”在一棵树中找到目标元素所需比较次数,等于元素所在树中的层级“,如果一棵树在满二叉树这样的理想状况下,查找的时间复杂度为 O(logn)。但是大部分时候,我们增删数据数据后,很难达到满二叉树的情况,甚至在某种极端情况下,它甚至会退化成链表,这样就会将查找的时间复杂度升级为 O(n)。
通常情况下,我们见到的树都是有高有低的,层次不齐的,如果一颗二叉树中,任意一层的结点个数都达到了最大值,这样的树称为满二叉树,一颗高度为 k 的二叉树具有 2k - 1 次个结点
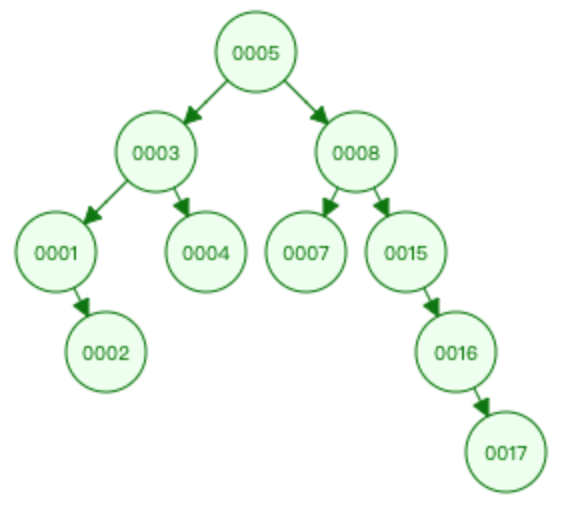
- 上图中,我们存储了 1、2、3、4、5、7、8、15、16、17 各元素,如果使用线性结构,例如查询 15 这个元素的位置,我们就需要遍历到第 8 个位置去,但是如果使用了二叉查找树,则只需要 3 次即可,即从 5-8-15(小的在左,大的在右)。
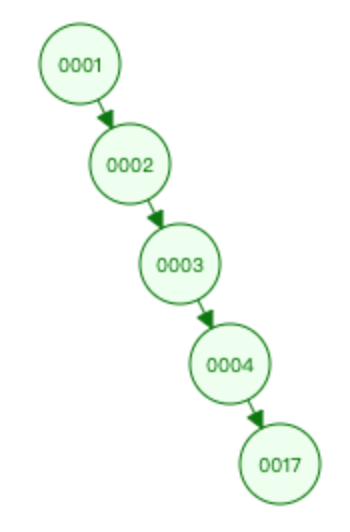
- 上图就是退化成链表的状态。
总之:225 = 33554432 大概 3000 多万的数据,如果通过线性结构遍历查询,那么平均也需要 1500 万次,但是如果通过二叉查找树(需要平衡,即满足二叉平衡树),最多也就 25 次,简直天壤之别。
2.2 二叉平衡树
二叉平衡树其实就是在二叉查找树的前提上,进行了约束,即左右子树高度差不能超过 1,保证了左右子树平衡。为了出现在二叉查找树中,树退化成链表的问题,二叉平衡树增删数据后需要进行额外的旋转操作,这也就意味着性能的损耗,但是其增删改查的复杂度都是 O(logn)。
上面我们就提到了,225 = 33554432 大概 3000 多万的数据,通过二叉查找树(需要平衡,即满足二叉平衡树),最多也就 25 次。
存在的问题?
看起来这么庞大的数据被压缩到了这个次数,确实很了不得,但是如果这 25 此操作是在内存中的,那么几乎时间可以忽略不计,几百,几千,几万 都不在话下,但是因为 MySQL 数据量很大,所以都会持久化在硬盘中,等需要的时候再加载需要的部分到内存中,这也就存在磁盘 IO 操作。
而对于一个应用来说,瓶颈一般都卡在了网络 IO(例如 Dubbo 调用),和磁盘 IO(数据库读写) 中,所以 25 次的 IO 操作还是较多。
2.3 B 树
如果考虑了 IO 的效率问题后,那么二叉平衡树也不算特别合适了,我们知道 25 是 225 的指数,那么是否可以通过增大底数,从而减少指数呢?
答案是肯定的,在值不变的前提下,225 的值,介于 315 和 316 之间,而 225 中的 2,其实代表了分的叉,2就代表二叉,如果增大这个 ”叉“,例如变成三叉,肯定会大幅减少指数的值。例如前面看到的,”三叉树“ 只需要 15 ~ 16 次 IO 操作。
所以得出结论,在增加 ”叉“ 的前提下,树的深度会大大降低,这也就是 B 树的来由。
所以例如三叉平衡树也可以叫做 “三阶B树”。
“N阶B树” 每个节点可以存 N-1 个数据(二叉平衡树每个节点只存1个数据),而且每个节点至多可以连接 N 个子节点。
这样的好处就是,每个节点存储的数据变多了,这样每次取出一个节点的数据,就能够带出多一些的数据,而这些数据已经加载到内存中了,就可以直接进行比较了。大大减少了 IO 次数。
如何存储 B树这种结构呢?例如下面一个三阶B树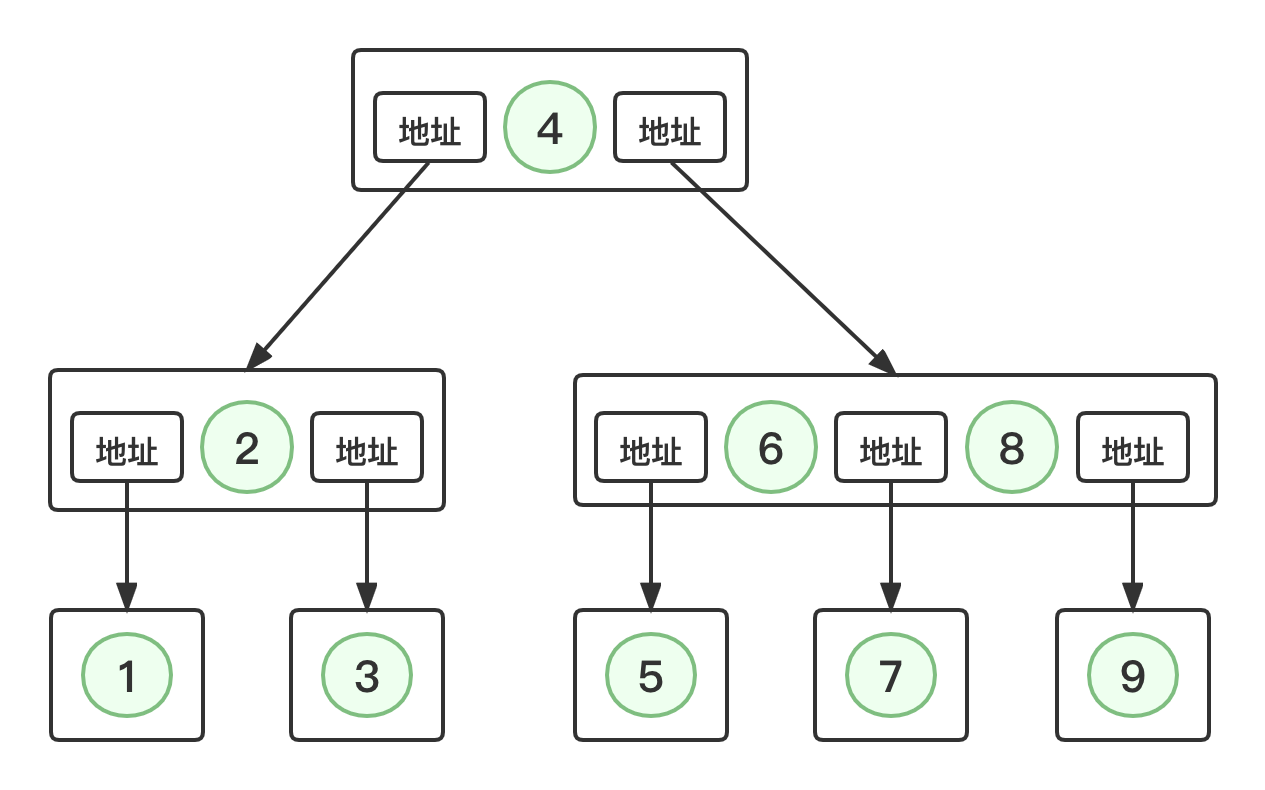
如上图所示,在每个节点中元素的左右两侧都会去存储地址,例如找 5 的时候,因为 5 > 4 ,所以会顺着 4 右侧的地址去找到右边含有 6 和 8 的节点,而 5 < 6 ,所以找到 6 左边的地址,从而顺着找到 5。
2.4 B+ 树
终于到 B+ 树了,可能大家会觉得,上面的 B 树已经不错了,那么为什么还要用 B+ 树。
首先我们先计算一下,一般来说,表中一行数据要占用多少字节。
前面的基础复习文章中,我已经讲过如何计算各种类型了。注:varchar(30) 代表最多能存储 30 个字符,中文字符的话,还需要乘以三,才能转换为字节。
整数类型
| 数据类型 | 占据空间 | 范围(有符号) | 范围(无符号) | 描述 |
|---|---|---|---|---|
| tinyint | 1 个字节 | -2^7 ~ 2^7-1 | 0 - 255 | 小整数值 |
| smallint | 2 个字节 | -2^15 ~ 2^15-1 | 0 - 65535 | 大整数值 |
| mediumint | 3 个字节 | -2^23 ~ 2^23-1 | 0 - 16777215 | 大整数值 |
| int | 4 个字节 | -2^31 ~ 2^31-1 | 0 - 4294967295 | 大整数值 |
| bigint | 8 个字节 | -2^63 ~ 2^63-1 | 0 - 18446744073709551615 | 极大整数值 |
小数类型
| 数据类型 | 占据空间 | 是够精确 |
|---|---|---|
| float | 4个字节 | 非精确 |
| double | 8 个字节 | 非精确 |
| decimal | 每4个字节存9个数字,小数点占一个字节 | 精确 |
时间类型
| 数据类型 | 占据空间 | 取值范围 |
|---|---|---|
| date | 3个字节 | 1000-01-01 ~ 9999-12-31 |
| time | 3~6个字节 | -838:59:59 ~ 838:59:59 |
| datetime | 5~8个字节 | 1000-01-01 00:00:00 ~ 9999-12-31 23:59:59 |
| timestamp | 4~7个字节 | 1970-01-01 00:00:01 ~ 2038-01-19 03:14:07 |
大家可以随便拟数据,结果可能不一致,我随便拟了一张,得到的结果大概 1000 多字节,我们统一按照 1000 计算。
而 MySQL 中和操作系统相似,也存在一个 “页” 的概念,简单的说,就是 B 树中每一个节点的空间,其大小为 16k。
而16k 除以 1k,也就意味着,我们一个节点最多能存储 16 行这样的数据。
所以二叉平衡树到 B树,在这种情况下,最多能每个节点多携带 15 个数据,但是这样看起来还是有限的,是不是可以继续优化呢?
为了尽可能多的在一个节点中塞入数据,从而使得整个树变矮,我们可以不在节点中存放全部数据,而是只存放数据的主键,例如一个 bigint 类型的主键占用 8 个字节 + 主键对应的地址指针占用 6 个字节,加起来就是 14。
16 * 1024 / 14 = 1170 个。
其实这就是 B 树到 B+ 树之间的优化。
小结:B+树,就是把原先B树中分散在各个节点的数据都写在最底层的叶子节点,非叶子节点只存储 “主键-地址” 形式的数据。

