进制
- 进制也就是进位制,是人们规定的一种进位方法
- 对于任何一种进制—X进制,就表示某一位置上的数运算时是逢X进一位
- 十进制是逢十进一,十六进制是逢十六进一,二进制就是逢二进一,以此类推,x进制就是逢x进位 | 十进制 | 二进制 | 八进制 | 十六进制 | | —- | —- | —- | —- | | 0 | 0 | 0 | 0 | | 1 | 1 | 1 | 1 | | 2 | 10 | 2 | 2 | | 3 | 11 | 3 | 3 | | 4 | 100 | 4 | 4 | | 5 | 101 | 5 | 5 | | 6 | 110 | 6 | 6 | | 7 | 111 | 7 | 7 | | 8 | 1000 | 10 | 8 | | 9 | 1001 | 11 | 9 | | 10 | 1010 | 12 | A | | 11 | 1011 | 13 | B | | 12 | 1100 | 14 | C | | 13 | 1101 | 15 | D | | 14 | 1110 | 16 | E | | 15 | 1111 | 17 | F | | 16 | 10000 | 20 | 10 |
二进制
- 二进制是计算技术中广泛采用的一种数制。二进制数据是用0和1两个数码来表示的数
- 它的基数为2,进位规则是“逢二进一”,借位规则是“借一当二”
- 当前的计算机系统使用的基本上是二进制系统,数据在计算机中主要是以补码的形式存储的
- 十进制转化二进制的方法:
- 用十进制数除以2,分别取余数和商数,商数为0的时候,将余数倒着数就是转化后的结果

口诀:除二取余,倒序排列法
八进制
- 八进制,Octal,缩写OCT或O,一种以8为基数的计数法,采用0,1,2,3,4,5,6,7八个数字,逢八进1
- 一些编程语言中常常以数字0开始表明该数字是八进制
- 八进制的数和二进制数可以按位对应(八进制一位对应二进制三位),因此常应用在计算机语言中
- 八进制和二进制互转:

- 十进制转化八进制的方法:
- 用十进制数除以8,分别取余数和商数,商数为0的时候,将余数倒着数就是转化后的结果

十六进制
- 十六进制(英文名称:Hexadecimal),同我们日常生活中的表示法不一样,它由0-9,A-F组成,字母不区分大小写
- 与10进制的对应关系是:0-9对应0-9,A-F(或a-f)对应10-15
- 十六进制的数和二进制数可以按位对应(十六进制一位对应二进制四位),因此常应用在计算机语言中
- 十六进制和二进制互转:

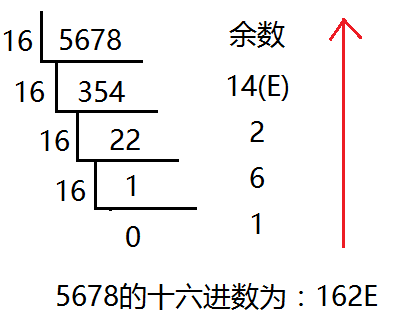
- 十进制转化十六进制的方法:
- 用十进制数除以16,分别取余数和商数,商数为0的时候,将余数倒着数就是转化后的结果
C语言如何表示相应进制数
| 十进制 | 以正常数字1-9开头,如15 |
|---|---|
| 八进制 | 以数字0开头,如017 |
| 十六进制 | 以0x或0X开头,如0xf |
| 二进制 | 以0b或0B开头,如0b1111 |
示例代码:
#include <stdio.h>int main() {// 十进制方式赋值int a = 15;// 八进制方式赋值int b = 017;// 十六进制方式赋值int c = 0xf;// 二进制方式赋值int d = 0b1111;printf("%d, %d, %d, %d\n", a, b, c, d);return 0;}
数值存储方式
计算机底层都是存储数据都是采用二进制,但二进制也有几种,比如:原码、反码、补码。接下来我们来看看他们之间的关系的意义作用。
原码
十进制数按照:除二取余、倒序排列,得到的就是原码。
- 10 -> 0000 1010
- -10 -> 1000 1010
- -1 -> 1000 0001
-
问题
原码在做计算的时候会出现一些问题,比如正负数的加法运算,以及零的问题。
正负数加法
- -1 + 1 = 0 ``` 1000 0001
+ 0000 0001
1000 0010 -> -2 ?
- 正负零- +0 和 -0- 十进制数字0,占了两个二进制;
0000 0000 1000 0000
<a name="qNFAT"></a>## 反码> 为了解决上面的问题,出现了反码,反码的计算规则如下:- 正数的反码就是原码本身;- 负数的反码是按位取反(但符号位不变);示例- 1 -> 0000 0001 -> 0000 0001- -1 -> 1000 0001 -> 1111 1110
0000 0001
+ 1111 1110
1111 1111
1111 1111 是运算完之后的结果,但要注意,这时还是**反码**,需要重新返回来:1000 0000 。<br />反码解决了**正负数加法**问题,但正负零的问题还是存在。<a name="usksS"></a>## 补码> 正数的补码就是原码本身;> 负数的补码就是在反码的基础上+1;- 1 -> 0000 0001 -> 0000 0001 -> 0000 0001- -1 -> 1000 0001 -> 1111 1110 -> 1111 1111
0000 0001
+ 1111 1111
0000 0000
补码在正负数加减法运算时没问题,也不会出现正负零占两个二进制。但 1000 0000 不表示为负零,用来表示什么呢?计算机其实默认把8位有符号二进制 1000 0000 表示为 -128 。```cint8_t e = 0b10000000;printf("%d\n", e);

