神经网络 [ANN]概述

感知器

首先神经网络是来自于人的思考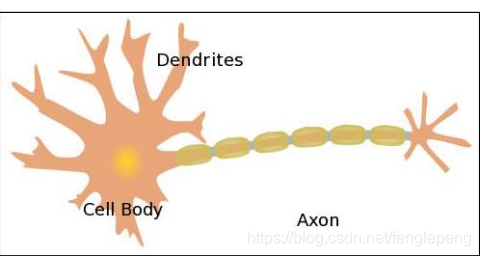
image.png
大脑是处理信息的神经元细胞和链接神经元之间的细胞进行信息传递的凸出构成的
树突【Dendrites】 这个是从神经元接受电信号的，信号在细胞核处理之后，通过轴突 将处理的信号传递给下一个神经元

那么我们可以将一个神经元看成一个或者多个处理成一个输出的计算单元，通过多个神经元之间的传递，最终大脑会得到这个消息，并且可以对于这个消息给出一个合适的反馈
那么我们模拟这个创建了一个简单的模型 来模式这个神经网络的模式

感知器【PLA】

感知器的模型：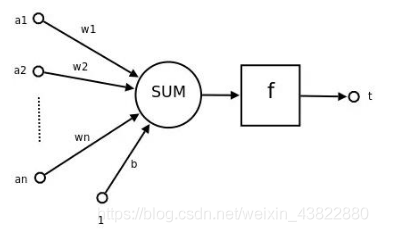
image.png
感知器的输出一般都是0或者1 这样可以实现对于矢量进行分类的目的
上面名词解释： n维向量的[a1,a2,a3—-an]的转置作为感知机的输入，[w1,w2—-wn]作为输入分类 连接到感知器的权重中，b 是偏置 【bias】 f() 是激活函数 , t 就是感知器的输出， 表达式如下：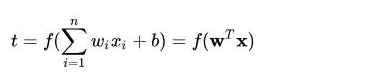
image.png
这里的f 其实是一个符号函数 : 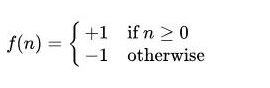image.png
那么我们可以化简更为 f(x) = sign(w*x + b)

激活函数

激活函数的作用主要是提供网络的非线性的建模能力，如果没有激活函数，那么该网络仅能表达线性映射，此时即便有再多的隐藏层，其中整个网络跟单层的神经网络也是等价的，因此，只有加入激活函数，深度神经网络才具备了分层的线性映射学习的能力，激活函数的主要特征： 可微性，单调性，输出值的范围。
详细可以看看这一片 关于激活函数的介绍 特别详细了： 激活函数

建立损失函数

我们神经网络训练的目的就是得到一个能够将训练集中正负实例完全分开的超平面， 那么如何找到这个超平面呢？ =》 确定超平面就是需要确定感知模型中的w以及b , 那么我们就需要定义一个损失函数通过这个函数的最小化来求w 以及b
这里选择失分点到分类超平面的总距离， 那么输入空间中任意一个点 x0到超平面S的距离就是: 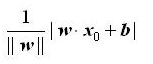image.png
其中 |||w|| 是w 的L2范数 也就是w 中每一个元素去平方然后相加开根号 也就是
image.png
对于失分点 (xi,yi) 到达超平面S 的距离就是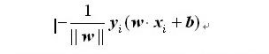
image.png
那么最终 我们的式子可以演化成为 这样：
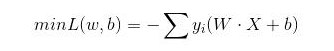
image.png
那么我们训练的过程就是不断的调整入参和出参以达到最终我们想要的结果
如此我们最后可以得出一个 e = t - a 如果t表示目标输出，a表示实际输出 训练的目标就是让 t - > a ; tips :: 只要网络表达的函数是线性可分的，那么函数经过有限次迭代之后，将收敛得到正确的权值和阈值， 这样就使得e=0

权重和阈值调整算法

image.png 其中p 时训练的输入向量和输出向量对来构成的， n 个训练的结果就是 {{p1,t1},{p2,t2},{p3,t3}….{pn.tn}}
参数解释： 其中w 就是权值向量，b 就是阈值向量，p 就是输入向量，k 就是第k步学习的过程
如果输入的向量的取值范围比较大一点，导致一些输入的值过大，而一些输入的值过小，按照上面这些式子训练的时间会比较久 为此阈值的调整我们可以使用上面的调整，而权值的调整我们可以采用归一化的方法也就是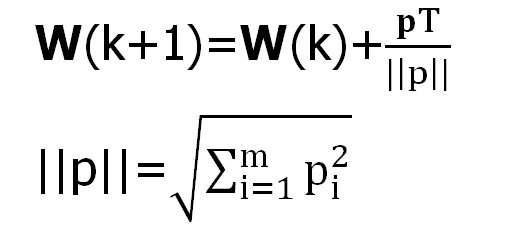： image.png tips: 这个训练方法可以通过函数 learnpin来实现

梯度下降

如果按照上述的训练方式 我们还可以对于我们训练完成的结果集进行优化 也就是梯度下降 【个人理解： 训练出来的点距离超平面的距离肯定是有大有小的 为此我们需要降低那些梯度比较高的地方 】
定义： 函数在某一点的梯度就是这样一个向量： 它的方向和取得最大方向一致，而它模的方向导数的最大值。 那么以山举例子，这里就是坡度最陡的地方，梯度值就是描述坡度有多陡
导数在直角坐标系中 就是一个函数的切点
偏导数就是n 维平面中一个平面对应在一个方向坐标系中对应的导数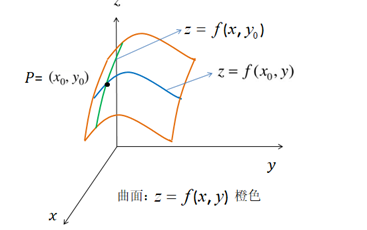
image.png
方向导数 因为偏导数是无法确定任意平面上其导数的方程 为此方向导数就是结合方向坐标系和偏导数得以求出该函数在任意平面上的导数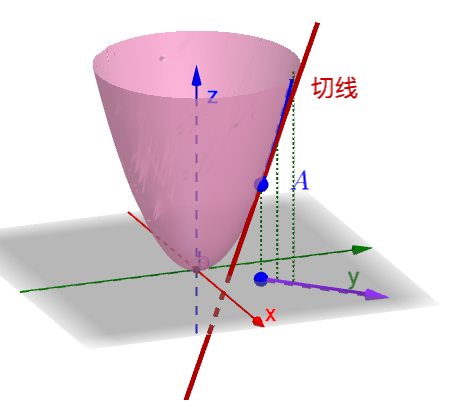
image.png

可以看看原文 ： 导数 偏导数 方向导数
那么梯度下降的方向就是梯度的反方向 也就是最小化损失函数L(w,b) 就是先求出函数在w 以及b 两个变量轴上的偏导数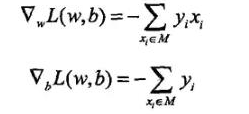image.png
可是我们更新一次参数都需要遍历整个的数据集，如果数据集非常大，那么肯定是不合适的，为了解决这个问题 我们只能随机选取一个误分的点来进行参数更新，这个就是随机梯度下降

随机梯度下降

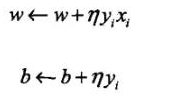
image.png
参数设置：
η 这里指学习率
η 太小函数拟合（收敛） 的过程就会 比较慢
η 太大容易在最低点的方向震荡 ， 进入死循环

算法总结

image.png

小例子

感知器可以看作是根据权重来做出决定的一个设备/单元，只要我们可以给定一个比较适合的权重以及阈值，那么感知器应该是能够对数据进行判断/分类预测的。
假定你现在在考虑是否换工作，也许你会考虑一下三个方面的因素：

  • 新工作的待遇会提高吗？ 权重w1
  • 你家庭经济压力大吗？ 权重w2
  • 新工作稳定吗？ 权重w3

结果：w1x1 + w2x2 + w3*x3 比较 阈值

那么感知神经元直观的逻辑与：
image.png
单个神经元的或的功能：
image.png

小例子

我们需要将不同两个颜色的点划分到统一区域 那么最简单的就是任意画一条对角线来分隔两组数据点，定义一个阈值以确定每个数据点属于哪一个组。
为此我们可以使用这样一个式子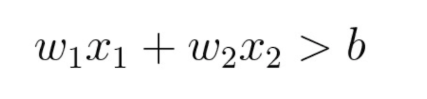： image.png 其中 b 是确定线的位置的阈值。通过分别为 x1 和 x2 赋予权重 w1 和 w2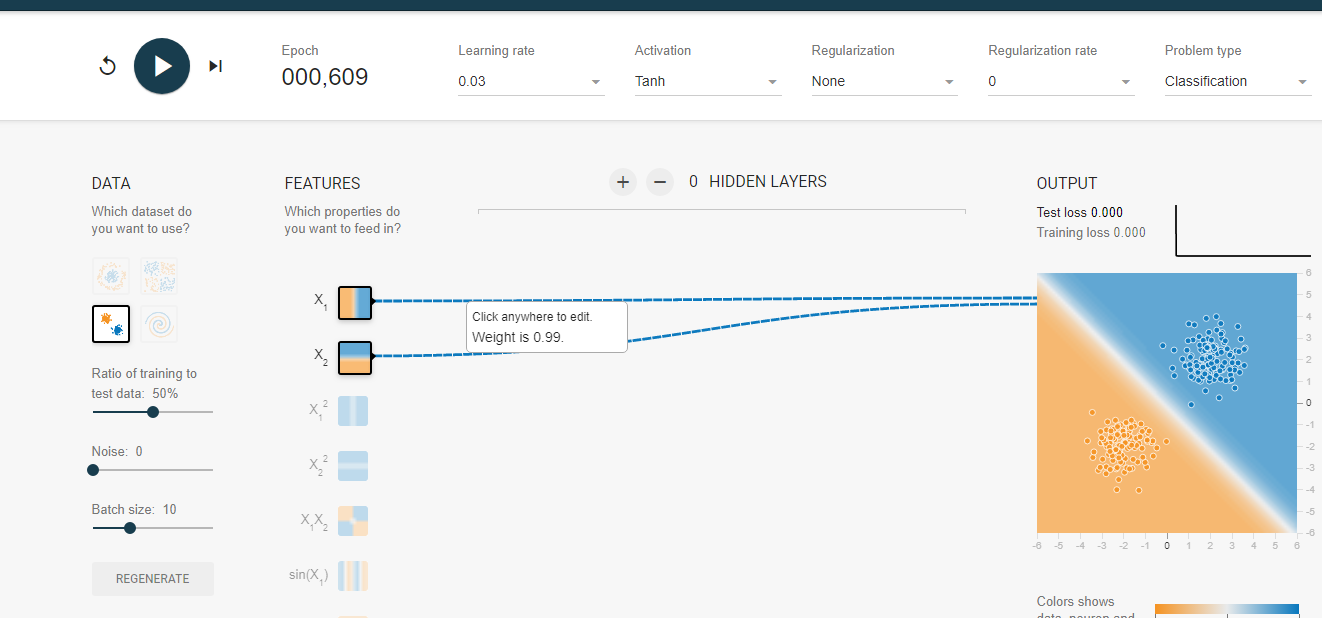
image.png

那么如果需要实现划分异或的点集呢？ 可以使用逻辑回归的方式来学习吗？
异或的点集以及训练结果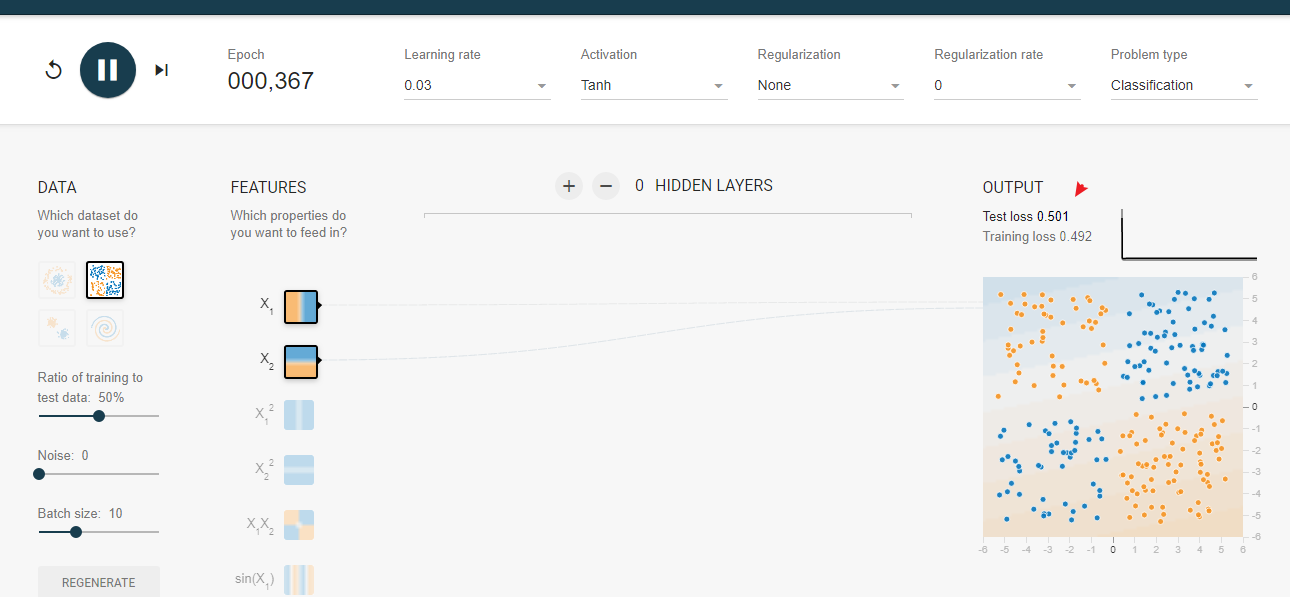
image.png 发现我们无法确立一个异或模型的输出
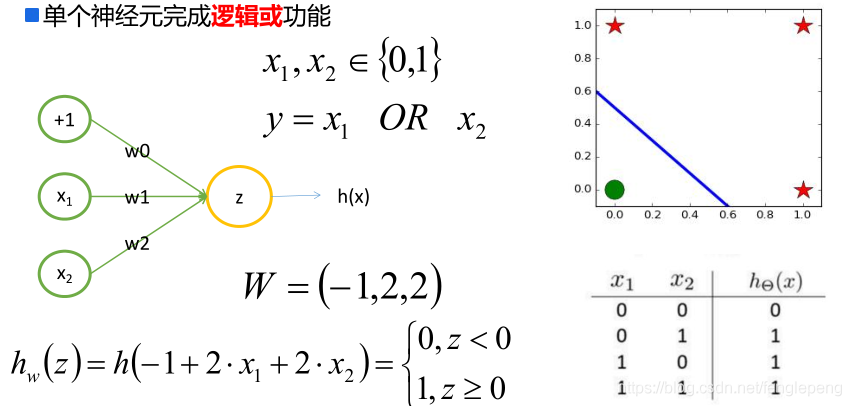
逻辑证明： 左上角点：x1=0，x2=1输出z=1 右上角点：x2=1，x2=1输出z=0 左下角点：x1=0，x2=0输出z=0 右下角点：x1=1，x2=0输出z=1
观察异或运算我们来看下面结果：
如果当X2=0， 将X1的取值从0到1，使得Z的结果也从0到1，意味着Z的变化时与X1正相关，需要设置A为正数
如果当X2=1， 将X1的取值从0到1，使得Z的结果也从1到0，意味着Z的变化时与X1负相关，需要设置A为负数
发现得到的结果居然是相悖的！！
解决方法： 其实只需要再加几层 就可以了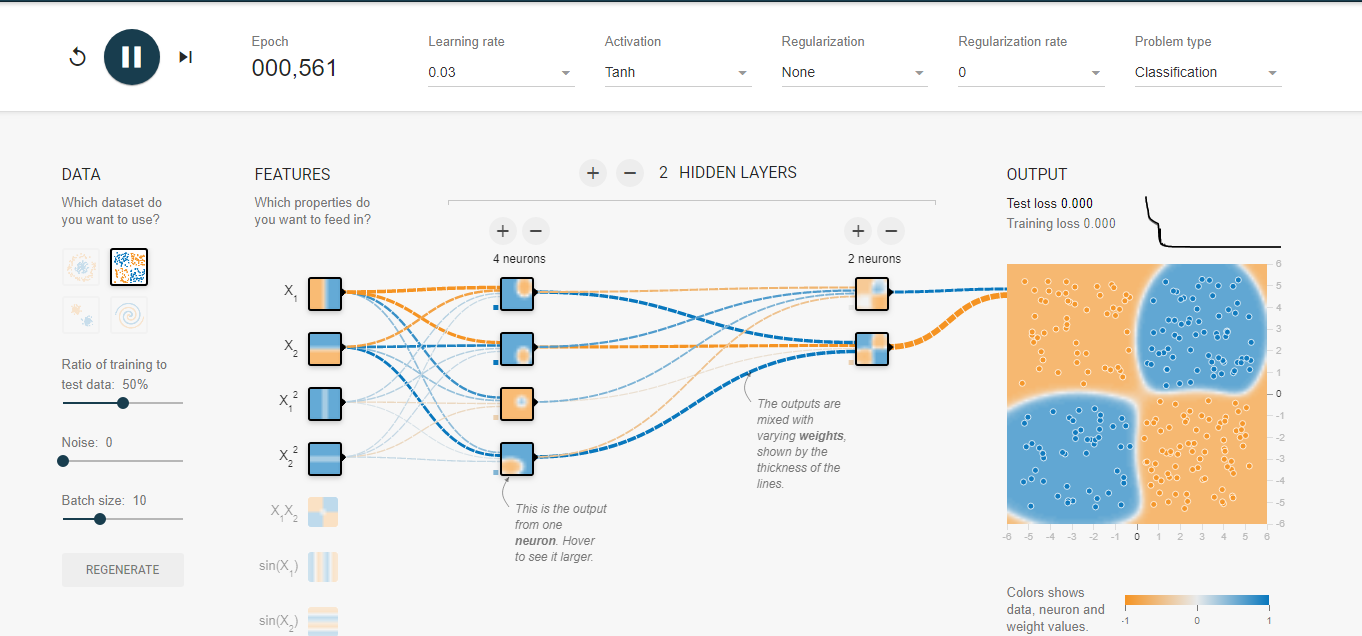
image.png

S型神经网络

对于感知器网络这样的问题，我们导入S型神经元来替换感知器，为此感知器模型+非连续激活函数来让网络服务非线性的因数方法就诞生了
在感知器模型中，我们可以把单个神经元的计算过程看成两个步骤：

  • 先计算权重w 以及 输入值x 以及偏置项b之间的线性结果值： z : z=wx+b
  • 然后对于结果z 进行一个数据的 sign 函数(变种) 转化得到了一个离散的0/1 的值y = int(sign(z) + 1)/2

image.png

神经网络

可以使用这个链接来查看训练的过程： playground
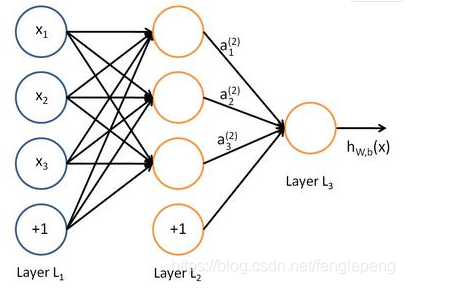
我们知道了前置知识之后来看神经网络的结构：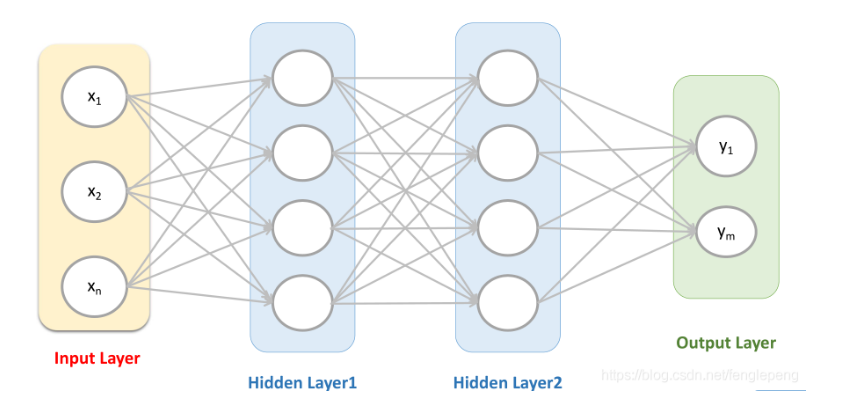
image.png
神经网络的组成部分：

  • 输入层：神经网络的第一层，原始的样本数据
  • 输出层：神经网络的最后一层，最终的计算结果
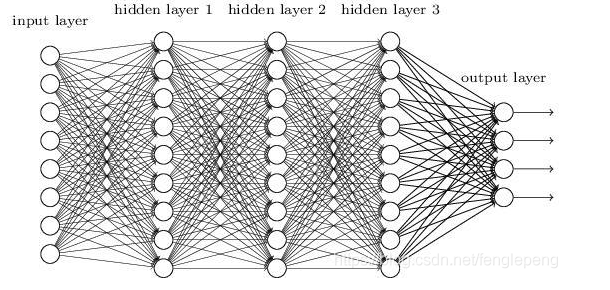
  • 隐藏层：其余的中间层都被称为隐藏层（hidden layer）
  • 权重（weight）：就是之前所说的参数，这里被称为一个神经节点的权重。
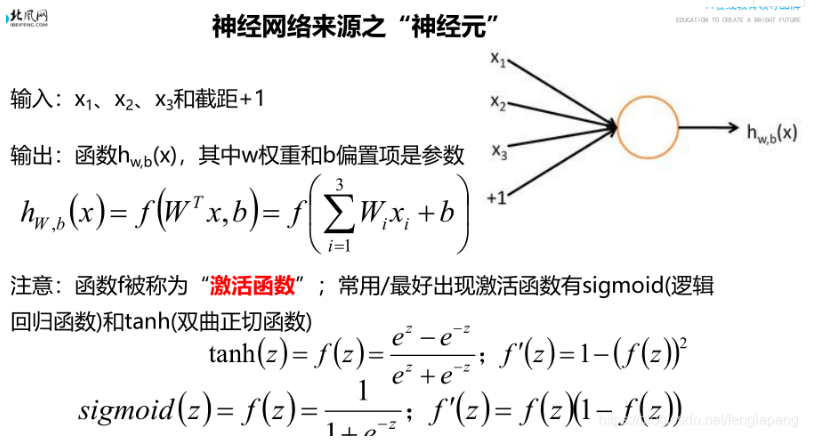
  • 激活函数（activation function）：激活函数是两层神经元之间的映射函数，是一种输出到输入的转换，一般是非线性的，而且是单调可微函数（因为优化方法是基于梯度的）。常见的激活函数有：sigmoid,tanh

神经网络又可以分为两种的类型

  1. 前馈型神经网络【Feedforward Neutral Networks】 这个是最常见的神经网络类型，一般定义是有向无环图，信号只能沿着最终输出的哪一个方向传播
  2. 反馈神经网络【Feedback Netural Networks】 这个是称为递归神经网络，或者网络中环

    浅层神经网络

    定义： 添加少量隐层的神经网络就是浅层神经网络，也是传统的神经网络
    image.png

    深度神经网络

    增多中间层【隐层】 的神经网络就是深度神经网络(DNN)
    image.png