本篇文章只作为对于图的知识点和图的方法做介绍。
图的基本概念
首先,了解一下图的一些定义的基本概念。
- 图的术语:顶点、边、邻接、关联、度、回路、路径、联通构件、生成树;
- 图的类型:无向图、有向图、加权图;
图
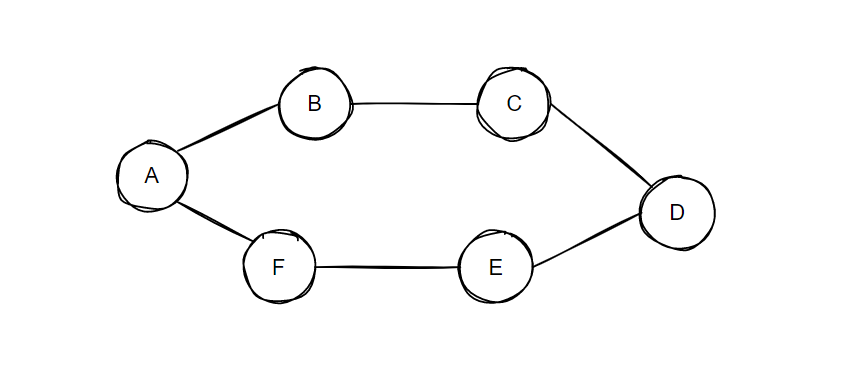<br />图是一个用线或者边连接在一起的**顶点**或者**节点**的集合,用以下公式表示:<br /><br />其中: <br />**V** (vertex)表示元素的**顶点**(也称为 **节点 ** 或者 **点**)。如上图所示,A B C都称为 **顶点**;<br />**E **(edge)表示元素的**边**(也称为 **弧** 或者 **线**)。每一条边连接两个不同的顶点,用元组表示,其中** _i _**和_ _**_j_**_ _是边所连接的两个顶点。如上图所示,边表示为(A, B);
在边 ( i, j ) 中,顶点 i 和 j 是 邻接 的, 边(i,j)关联 于顶点 i 和顶点 j。
图的类型
从边的方向看,图分为:
- 有向图;
- 无向图;
从边的权重看,图分为:
- 加权图;
- 无权图;
顾名思义,全部由 无向边 构成的图,称为 无向图,全部由 有向边 构成的图,称为 有向图;如下图所示,左侧的无向图可以看出,各个顶点相互连接的边都是没有方向的。右侧的有向图可以看出,各个顶点相互连接的边是有方向的。
在目标搜索中,无向图表示在图中的所有顶点,只要边是存在的,则两个点之间必是可以通行的;而有向图表示,在图中的所有顶点,两个点之间是否可以通行,还取决于边的方向。在下图的有向图中,顶点A不能到达顶点B,而顶点B可以到达顶点A;顶点B和顶点C可以双向通行。

在图的应用中,有些可能需要给边加上一些成本的计算,称之为 权 。边(A, B) 的权表示从顶点A到达顶点B需要的成本,例如时间成本2min。
上图所示的无向图和有向图,亦可称之为无权的无向图和有向图。下图所示的便是 加权无向图 和 加权有向图。无权的有向或者无向图可以看成是特殊形式的加权图,只是每个边的权重是一样的。
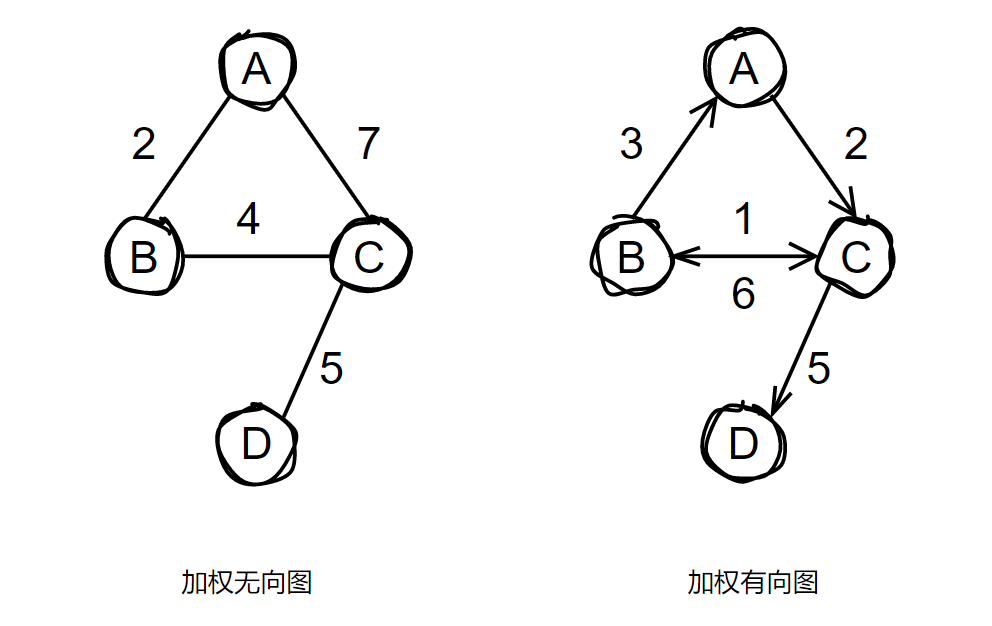
对于有向图,邻接和关联有更加精确的定义。
在无向图中,我们称边 ( i, j ) ,顶点 i 和 j 是 邻接 的, 边(i,j)关联 于顶点 i 和顶点 j。而在有向图中,有向边 ( i,j ) 是 关联至 顶点 j 而 关联于 顶点 i。 顶点 i 邻接至 顶点 j , 顶点 j 邻接于 顶点 i。
无论是有向图还是无向图,一个图中,不能有重复的边。在上图无向图中,顶点B 和顶点 C有且只有一条边,而在有向图中,B 和 C 表示的是两个不同的边,分别是 (B, C)和(C, B)。
一个图中不能出现 自连边 ,即(i,i)。自连边也称为 环 。
度
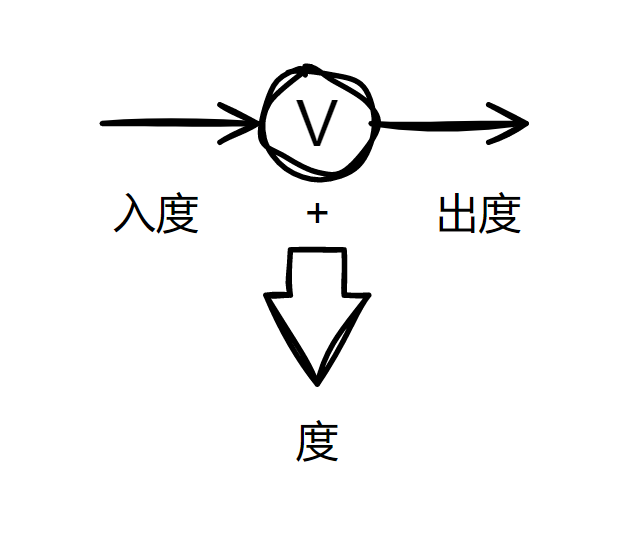
度是对于一个顶点边的描述。度是出度和入度的和。
- 度:指的是与该顶点相连接的边的个数;
- 出度:出度是针对于有向图顶点的描述。在有向图中,以该顶点出发的边的条数总和,称为该顶点的出度;
入度:入读是指向该顶点的边的条数总和。
生成树
连通:在一个图中,每个顶点之间或是直接、或者间接的与每个顶点相互连通,则称为该图是连通的;
我们称下面的图是连通的。顶点A,B,C之间直接相通,而顶点B和顶点D可以通过 B -> C -> D 的方式相通。

- 环路:一条起点和终点相同的简单路径称为环路;
树:没有环路的连通无向图是一棵树;
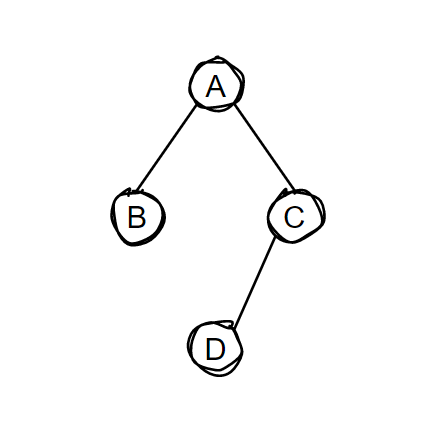
子图:如果图 H 的顶点和边的集合分别是图 G 的顶点和边的集合的子集,那么称图 H 是图 G 的子图;
在下图中,图 G 的两个子图 图 H 和 图 F .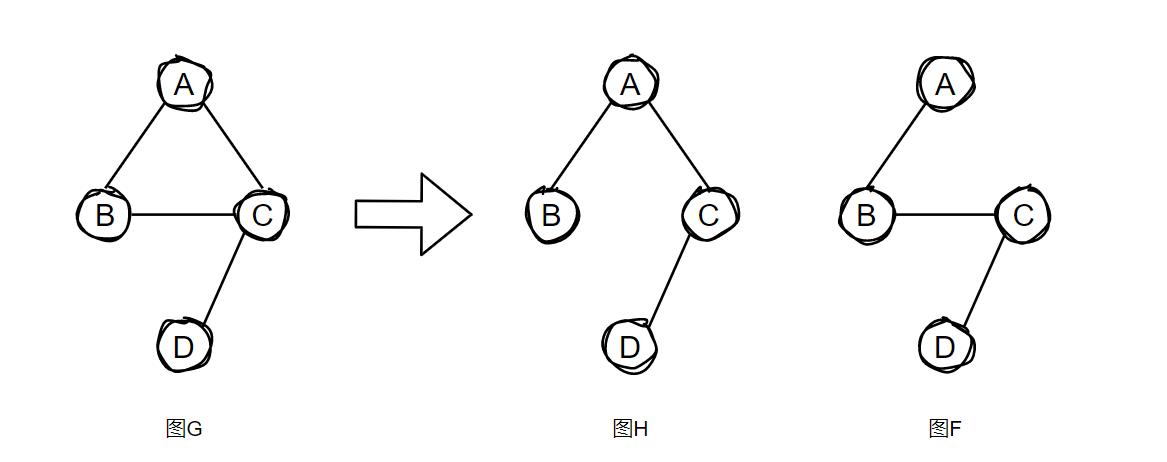
对于图 G 的描述为:
对于图 H 的描述为:
对于图 F 的描述为:
- 生成树:一个树的子图,如果包含图 G 的所有顶点,且是一棵树,则称为 G 的生成树。
图的描述
图分为无权图和加权图。
- 无权图的描述:
- 邻接矩阵;
- 邻接链表;
- 邻接数组;
- 加权图的描述:
- 成本邻接矩阵;
无权图的描述
邻接矩阵
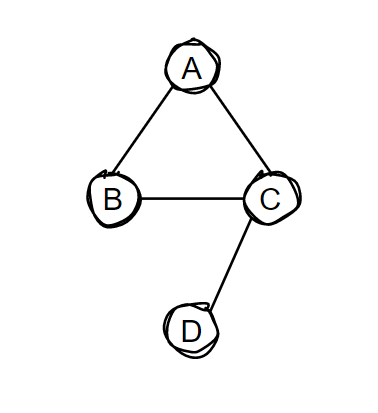<br />对于上面的图,记为图G。图 G 有4 个顶点,则描述该图的矩阵是一个 4 x 4 的矩阵,记为矩阵A。在矩阵A中,存在顶点之前直接连通的元素值为1,否则为0。因此,矩阵元素的定义如下:<br /> 
邻接矩阵的形式如下:
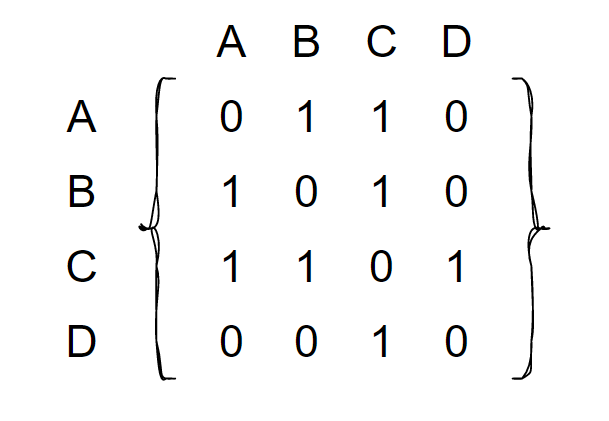
观察上面的邻接矩阵,可以发现,邻接矩阵是对称的,因此只需要存储上三角或者下三角的元素,所需的空间是 个字节,可以减少 50% 的存储空间。
邻接链表
邻接链表的形式,是先将图中所有的顶点先存入到一个线性的邻接表中,再把邻接表中的顶点作为每一个新的邻接表,用来链接与顶点相邻接的点。

还是这个图G。定义每个顶点为一个链表的节点。其中节点中包含了顶点的编号以及指向下一个节点的指针。

图G的邻接链表的表现形式如下图所示。
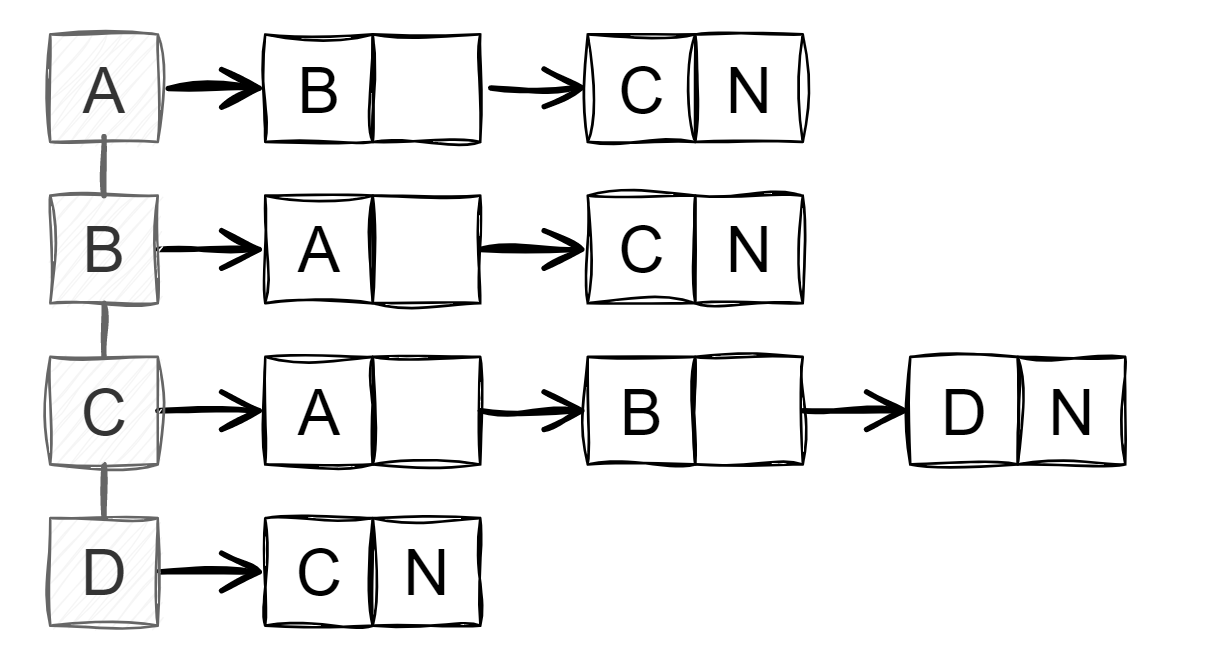
邻接数组
加权图的描述
邻接矩阵
相比于无权的矩阵元素值 0 和 1,加权的矩阵元素值就是边的权重,而对于不邻接的两个顶点,元素值用 “ - ”表示。

现有如上所示的加权无向图,图 G 。用边的权重作为矩阵元素的元素值,其矩阵的表示如下所示。
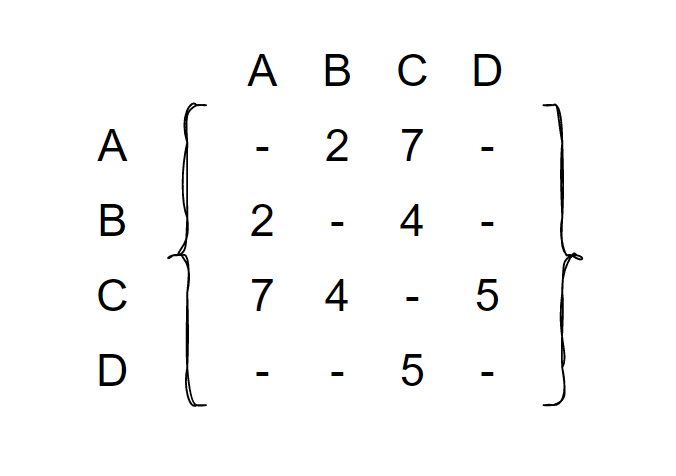
另有如下所示的加权有向图,其邻接矩阵的表示如下:

邻接链表
无权无向图的链表节点多了个元素,代表了当前邻接的边的权重。
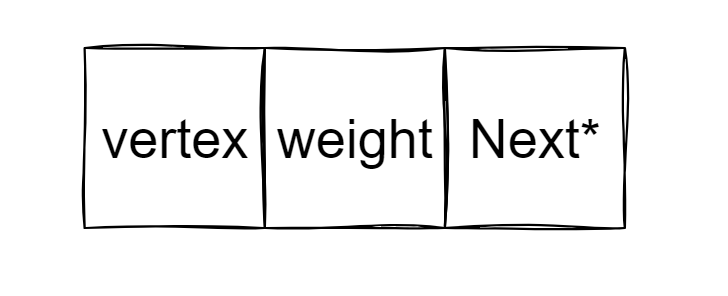

图的遍历
图的遍历有广度优先和深度优先算法。
移步至 广度和深度搜索算法。

