介绍

广度优先搜索算法（Breadth-First Search，BFS）会以相关联的节点展开的方式，系统性的遍历所有的节点，直到找到目标节点为止。

广度优先搜索是一种盲目的搜索算法，但是仍能找出两点间最短的路径。

搜索流程

有图如上所示，图的顶点 A B C D E F G。现在假设以顶点 A 作为起点，顶点 D 作为终点，算法的搜索步骤如下：

起点 A 扩展出两个邻接的顶点，分别是顶点 B 和顶点 G。标记已扩展节点。在扩展出的顶点里，没有目标顶点；
继续扩展刚扩展出的顶点。
1. 顶点 B 扩展出邻接的顶点 C 和顶点 F；
2. 顶点 G 扩展出邻接的顶点 E 和顶点 F；
3. 顶点 F 会在第一次被扩展后标记为已扩展，所以 B 或者 G 理论上只有一个顶点能扩展到 F，由扩展顺序决定；
4. 在扩展出的顶点里，仍没有目标顶点；
此时，顶点 F 没有未扩展节点，顶点 C 和顶点 E 能扩展到顶点 D，扩展得到顶点 D 就是此次搜索的目标顶点。得到路径 A -> B -> C -> D 或 A -> G -> E -> D 。

队列

我们要遍历的是与顶点邻接的顶点，要求遍历完当前顶点的邻接顶点后马上就遍历邻接顶点的新的邻接顶点。因此，队列（Queue）是最符合当前运用场景的。

队列是一种特殊的线性表。队列的操作方式为从队列尾部插入，从队列的头部弹出。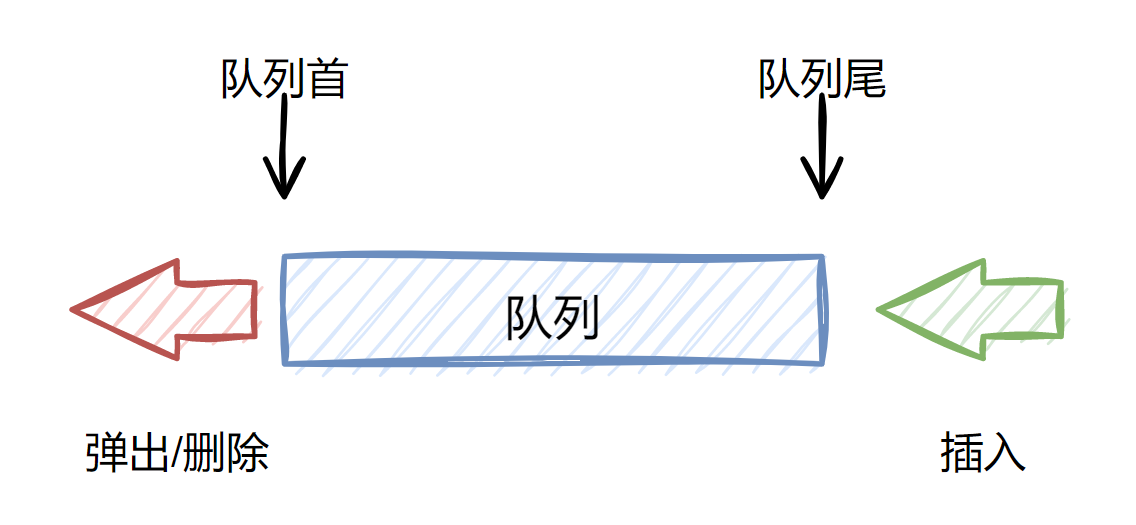

可以使用 C++ STL 库提供的 queue 实现。

伪代码

以下伪代码的实现遍历图上所有的顶点。

广度优先搜索算法(起点v)
{
    标记起点v为已遍历;
      初始化队列Q;
    将起点v插入到队列里;
    while(Q非空)
    {
            从队列中弹出顶点w;
        获取顶点w的邻接顶点u;
        while(u != NULL)
        {
                if (顶点u未被遍历)
            {
                    添加u到队列中;
                标记u已遍历;
            }
            获取顶点w的另一个邻接顶点u;
        }
    }
}

以下稍作修改，利用广度优先搜索算法寻找终点。

广度优先搜索算法(起点v, 终点u)
{
    标记起点v为已遍历;
      初始化队列Q;
    将起点v插入到队列里;
    while(Q非空)
    {
        从队列中弹出顶点w;
        获取顶点w的邻接顶点n;
        设置n的父节点为w；
        if (顶点n 是 终点u)
        {
            结束获取，返回终点;
        }
        while(n != NULL)
        {
            if (顶点n未被遍历)
            {
                添加n到队列中;
                标记n已遍历;
            }
            获取顶点w的另一个邻接顶点n;
        }
    }
}
获取路径(起点v, 终点u)
{
    定义并初始化一个队列Q；
    将终点u插入到队列里;
    将终点u设置为当前顶点；
    while(当前顶点的父顶点 != nullptr)
    {
        将当前顶点的父顶点插入到队列里;
        设置父顶点为当前的顶点;
    }
    返回队列Q为当前的最佳路径;
}

代码

以一个 10 x 10 的栅格地图为例。

#include <iostream>
#include <queue>
#include <cstring>
/* 0:不可通行 */
/* 1:可通行 */
uint8_t map[10][10]
{
    {1, 1, 1, 1, 1, 1, 1, 1, 1, 1},
    {1, 1, 1, 1, 1, 1, 1, 1, 1, 1},
    {1, 1, 1, 1, 1, 1, 1, 1, 1, 1},
    {1, 1, 1, 1, 1, 1, 1, 1, 1, 1},
    {1, 1, 1, 1, 1, 1, 1, 1, 1, 1},
    {1, 1, 1, 1, 1, 1, 1, 1, 1, 1},
    {1, 1, 1, 1, 1, 1, 1, 1, 1, 1},
    {1, 1, 1, 1, 1, 1, 1, 1, 1, 1},
    {1, 1, 1, 1, 1, 1, 1, 1, 1, 1},
    {1, 1, 1, 1, 1, 1, 1, 1, 1, 1},
};
struct Vertex
{
    uint8_t x, y;
    uint16_t pre;
    bool reached;
}; 
uint8_t * closeMap = nullptr;
bool breadthFirstSearch(Vertex start, Vertex end)
{
    std::queue<Vertex> mList;
    mList.push(start);
    int index = start.y * 10 + start.x;
    closeMap[index] = 1;
    while(mList.empty() == false)
    {
        Vertex w = mList.front();
        mList.pop();
        for (int i = -1; i <= 1; i ++)
        {
            int ii = w.x + i;
            for (int j = -1; j <= 1; j ++)
            {
                int jj = w.y + j;
                int ww = jj * 10 + ii;
                if (ii >= 0 && jj >= 0 && ii < 10 && jj < 10)
                {
                    if (map[ii][jj] == 1)
                    {
                        if (closeMap != nullptr)
                        {
                            if (closeMap[ww] == 0)
                            {
                                Vertex n;
                                n.x = ii;
                                n.y = jj;
                                n.pre = (uint16_t)((ii << 4) | (jj));
                                mList.push(n);
                                closeMap[ww] = 1;
                            }
                        }
                    }
                    if (ii == end.x && jj == end.y)
                    {
                        return true;
                    }
                }                
            }
        }
    }
    return false;
}
int main(int argc, char * argv[])
{
    printf("hello world\r\n");
    closeMap = new uint8_t[100];
    memset(closeMap, 0, sizeof(uint8_t) * 100);
    Vertex start_p;
    start_p.x = 1;
    start_p.y = 1;
    Vertex end_p;
    end_p.x = 8;
    end_p.y = 8;
    if (breadthFirstSearch(start_p, end_p))
    {
        printf("bfs success\r\n");
    }
    else
    {
        printf("bfs failed\r\n");
    }
    delete [] closeMap;
    return 1;
}