路径规划之A*的启发函数

关于A的介绍，可以移步到这里。
本文参考[Amit`s A Pages](http://theory.stanford.edu/~amitp/GameProgramming/Heuristics.html)。

在 A 的介绍中，我们提到A是通过计算节点的代价成本来寻找当前的最佳路径。而A优于其他搜索算法的原因就是A的启发函数。

启发函数计算的是从当前节点到目标节点的一个预估成本。其实也就是从当前位置到目标位置的移动距离，预估的距离越准确，A搜索的路径就越优，因此启发函数的结果对A路径规划的结果也起了重要的影响。

启发函数计算值	函数	搜索结果
%3C%2Ftitle%3E%0A%3Cdefs%20aria-hidden%3D%22true%22%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-68%22%20d%3D%22M137%20683Q138%20683%20209%20688T282%20694Q294%20694%20294%20685Q294%20674%20258%20534Q220%20386%20220%20383Q220%20381%20227%20388Q288%20442%20357%20442Q411%20442%20444%20415T478%20336Q478%20285%20440%20178T402%2050Q403%2036%20407%2031T422%2026Q450%2026%20474%2056T513%20138Q516%20149%20519%20151T535%20153Q555%20153%20555%20145Q555%20144%20551%20130Q535%2071%20500%2033Q466%20-10%20419%20-10H414Q367%20-10%20346%2017T325%2074Q325%2090%20361%20192T398%20345Q398%20404%20354%20404H349Q266%20404%20205%20306L198%20293L164%20158Q132%2028%20127%2016Q114%20-11%2083%20-11Q69%20-11%2059%20-2T48%2016Q48%2030%20121%20320L195%20616Q195%20629%20188%20632T149%20637H128Q122%20643%20122%20645T124%20664Q129%20683%20137%20683Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-28%22%20d%3D%22M94%20250Q94%20319%20104%20381T127%20488T164%20576T202%20643T244%20695T277%20729T302%20750H315H319Q333%20750%20333%20741Q333%20738%20316%20720T275%20667T226%20581T184%20443T167%20250T184%2058T225%20-81T274%20-167T316%20-220T333%20-241Q333%20-250%20318%20-250H315H302L274%20-226Q180%20-141%20137%20-14T94%20250Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-6E%22%20d%3D%22M21%20287Q22%20293%2024%20303T36%20341T56%20388T89%20425T135%20442Q171%20442%20195%20424T225%20390T231%20369Q231%20367%20232%20367L243%20378Q304%20442%20382%20442Q436%20442%20469%20415T503%20336T465%20179T427%2052Q427%2026%20444%2026Q450%2026%20453%2027Q482%2032%20505%2065T540%20145Q542%20153%20560%20153Q580%20153%20580%20145Q580%20144%20576%20130Q568%20101%20554%2073T508%2017T439%20-10Q392%20-10%20371%2017T350%2073Q350%2092%20386%20193T423%20345Q423%20404%20379%20404H374Q288%20404%20229%20303L222%20291L189%20157Q156%2026%20151%2016Q138%20-11%20108%20-11Q95%20-11%2087%20-5T76%207T74%2017Q74%2030%20112%20180T152%20343Q153%20348%20153%20366Q153%20405%20129%20405Q91%20405%2066%20305Q60%20285%2060%20284Q58%20278%2041%20278H27Q21%20284%2021%20287Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-29%22%20d%3D%22M60%20749L64%20750Q69%20750%2074%20750H86L114%20726Q208%20641%20251%20514T294%20250Q294%20182%20284%20119T261%2012T224%20-76T186%20-143T145%20-194T113%20-227T90%20-246Q87%20-249%2086%20-250H74Q66%20-250%2063%20-250T58%20-247T55%20-238Q56%20-237%2066%20-225Q221%20-64%20221%20250T66%20725Q56%20737%2055%20738Q55%20746%2060%20749Z%22%3E%3C%2Fpath%3E%0A%3C%2Fdefs%3E%0A%3Cg%20stroke%3D%22currentColor%22%20fill%3D%22currentColor%22%20stroke-width%3D%220%22%20transform%3D%22matrix(1%200%200%20-1%200%200)%22%20aria-hidden%3D%22true%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-68%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-28%22%20x%3D%22576%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-6E%22%20x%3D%22966%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-29%22%20x%3D%221566%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3C%2Fsvg%3E#card=math&code=h%28n%29&id=RD2EY) = 0	A*算法退化成Dijkstra	仅能保证可以找到一条最优路径
<= 实际代价	越小，A*扩展的节点越多，运行的速度越慢	保证能找到一条最优路径
= 实际代价	最优状态，仅寻找最佳路径，不扩展别的任何节点	保证能找到一条最优路径，而且运算速度很快
>= 实际代价	容易扩展到其他节点	不能保证找到一条最佳路径，但是运算最快
	此时只有影响结果，A*变成BFS

因此，我们需要根据不同的使用场景，来设计不同的启发函数。如果你想要有更快的运行速度，那就设计一个更大的启发函数，但是你就得牺牲结果，A找到的可能就不是一条最短的路径；如果你想要最短的路径，那就设计一个小点的启发函数，但是你就得牺牲运行时间。最佳的效果是无限的逼近实际的代价，这样A就既能得到一个最佳路径，又不会浪费过多时间。

栅格地图中的启发函数

在栅格地图中，有几个广为人知的启发函数可以使用。

在栅格地图中，不同的移动方式应该匹配不同的启发函数：

• 如果移动方向是四邻域的，那应该使用曼哈顿距离去计算启发函数；
• 如果移动方向是八邻域的，那应该使用对角线距离去计算启发函数；
• 如果是在正方形网格上任意方向移动的，则可能需要欧几里得距离，但是如果在网格上找路径，但不在网格上移动，那就得需要考虑其他的计算方式了；
• 如果是在六边形网格上移动，具有6个方向，则可以用适合六边形网格的曼哈顿距离；

在计算的时候，必须保证和计算的单位是一致的。例如，如果是以米为单位进行测量的，距离为3个方格，每个方格10米，则启发函数的预估成本应该是 米。如果是以分钟为单位进行测量的，距离3个方格，每个方格移动需要5分钟，则启发函数的预估成本应该是 分钟。

曼哈顿距离

欧几里得距离标明两个点在标准的坐标系上的绝对轴的距离总和，即：

                                                      ![](https://cdn.nlark.com/yuque/__latex/4a7fce422f216f31f43cf88cc21d5842.svg#card=math&code=distance%20%3D%20dx%20%2B%20dy%3B&id=ljXwO)

曼哈顿距离的计算方式适用于只有四个方向可移动的场景中。即，你的移动方向是四邻域的，那么曼哈顿距离是最佳的选择。

D 表示的是移动方块的权重，你可以设置它为10或者1都可以。

对角线距离

如果你的地图允许对角线移动，则需要用一个不同的启发函数，对角线距离。
对角线距离又称为切比雪夫距离（wiki），表示两个点之间的距离定义为其各坐标数差值的最大值。
假设直线移动和对角线移动的代价成本都是D，则

                                  ![](https://cdn.nlark.com/yuque/__latex/4a62eda98819ccf600515a518ccc9c32.svg#card=math&code=%5Cbegin%7Balign%7D%20%0Adx%20%26%20%3D%20abs%28node.x%20-%20dest.x%29%20%5C%5C%0Ady%26%3Dabs%28node.y%20-%20dest.y%29%20%5C%5C%0Ah%28n%29%26%3D%5Cleft%28D%20%2A%20max%28dx%2C%20dy%29%5Cright%29%5C%5C%20%20%0A%5Cend%7Balign%7D&id=o5HOD)

但是，如果对角线运动的代价不是，则是类似于，那么，更准确的对角线距离计算公式应该是：

欧几里得距离

如果是可以沿任意角度移动（而不是网格方向），那么也许可以使用直线距离。

                             ![](https://cdn.nlark.com/yuque/__latex/c3bc6709ce8f018f40eb2b92f9133b0c.svg#card=math&code=%5Cbegin%7Balign%7D%20%0Adx%20%26%20%3D%20abs%28node.x%20-%20dest.x%29%20%5C%5C%0Ady%26%3Dabs%28node.y%20-%20dest.y%29%20%5C%5C%0Ah%28n%29%26%3DD%20%2A%20%5Csqrt%7Bdx%20%2A%20dx%20%2B%20dy%20%2A%20dy%7D%5C%5C%20%20%0A%5Cend%7Balign%7D&id=suewp) 

使用欧几里得距离计算的距离会比曼哈顿或者对角线距离还短，但是还是可以得到一个最短路径，只是将耗费更多的时间。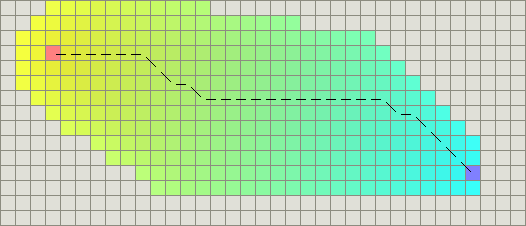

平方后的欧几里得距离

也有通过对距离的平方来避开欧几里得距离中的平方根计算，为了机器计算时的运算时间。

                                ![](https://cdn.nlark.com/yuque/__latex/bbd8c3dff080f5d49ec9ade44bf7e130.svg#card=math&code=%5Cbegin%7Balign%7D%20%0Adx%20%26%20%3D%20abs%28node.x%20-%20dest.x%29%20%5C%5C%0Ady%26%3Dabs%28node.y%20-%20dest.y%29%20%5C%5C%0Ah%28n%29%26%3DD%20%2A%20%28dx%20%2A%20dx%20%2B%20dy%20%2A%20dy%29%5C%5C%20%20%0A%5Cend%7Balign%7D&id=vSKqX)

但是不要这么做，这会明显的导致衡量单位的问题。此时的计算将会使得的结果恒大于，将会导致因为启发式函数评估值过高而停止。对于较长的距离，这将到接近的极值，而并不影响，而A*将退化成BFS。

Breaking Ties（打破平局）

在一次的搜索过程中，可能会有存在多个相同的，他们都会被搜索。因此出现了在搜索对比中的平局的局面。
解决这个问题，可以为启发函数增加一个附加值。附加值对于结点必须是确定性的（也就是说，不能是随机数），而且它必须让的值体现差异。
在上增加一个衡量单位 p 值。

选择因子p使得p < 移动一步（step）的最小代价的最长路径长度
假设不希望路径超过1000步，可以使 p = 1 / 1000
添加这个附加值的结果是，A比以前搜索的结点更少了

当存在障碍物时，当然仍要在他们周围寻找路径，但是当越过障碍物之后，A搜素的区域将非常少。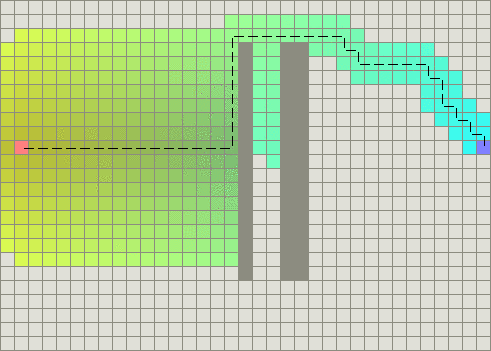

当然，对于要打破局面的做法，还有一个更直接的方法。
如果对于两个相同的结果，那么可以对比的值，以此来打破这个平局（breaking ties）。
还有另外一种方法，就是在启发式函数上添加一个确定性的随机数，这个随机数时计算坐标的哈希值。
第四种解决这个问题的方法。
对于启发式函数的计算，选择从初始点到目标点的连线。

对于这样的方法，A在选择路径时会稍微更倾向于从初始点到目标点的直线，当没有障碍物时，A不仅搜索的区域很少，而且它找到的路径看起来也非常的棒。

然而，因为这种方法是更倾向于起点到终点的直线连接，因此当出现了障碍物时，就会出现很奇怪的现象。