个人理解 :::info 1.可以根据上一个或几个状态递推出来
2.1维和2维的区别是有几个未知参数【不一定】
3.形式如不用个例子列举，只得出一个结果优先考虑动态规划，不行就递归 :::

Case 1 滚动数组式动态规划

大富翁游戏，玩家根据骰子的点数决定走的步数，即骰子点数为1时可以走一步，点数为2时可以走两步，点数为n时可以走n步。求玩家走到第n步（n<=骰子最大点数且是方法的唯一入参）时，总共有多少种投骰子的方法。

分析 1 骰子🎲一个有六种可能，其实可优化为1维数组

含义 可能的骰子 状态1【用于累加】 n = 1 n = 2 n = 3 n = 4
每次都是1 1 1 1 1 1 1
包含12 2 1 1 2 3 5
包含123 3 1 1 2 4 7
包含1234 4 1 1 2 4 8
包含12345 5 1 1 2 4 8
包含123456 6 1 1 2 4 8

状态转移方程
i-j >= 0 dp[i] = dp[i-j] j是1-6的累加和 【滚动数组源于不用使用前一个状态的结果】
例如 当骰子🎲只会出现1，2面时 n=4 可以有 n = 3 状态 和 n = 2 的状态 累加
当骰子🎲只会出现1，2，3面时 n=4 可以有 n = 3 状态 和 n = 2 的状态 和 n = 1的状态累加

  1. public class Main {
  2.     public static void main(String[] args) {
  3.         System.out.println(new Main().kind(3));
  4.     }
  6.     int kind(int n){
  7.         int[] dp = new int[n+1];
  8.         dp[0] = 1;
  9.         for (int i = 1; i <= n; i++) {
  10.             for (int j = 1; j <= 6; j++) {
  11.                 if (i-j >= 0)
  12.                     dp[i] = dp[i] + dp[i-j];
  13.             }
  14.         }
  15.         return dp[n];
  16.     }
  17. }

Case 2 笔试场景动态规划

有n个积木，每个积木长读为2，要在长度为k的空地上将这些个积木摆放下来。每一个积木必须摆放在前一个积木之上（也就是摆放在它前一格或后一格），问一共有多少种摆法，结果对998244353取模。

分析 1 第i个木块可能有两个选择，⬅️上角和➡️上角，此外需要考虑k的边界限制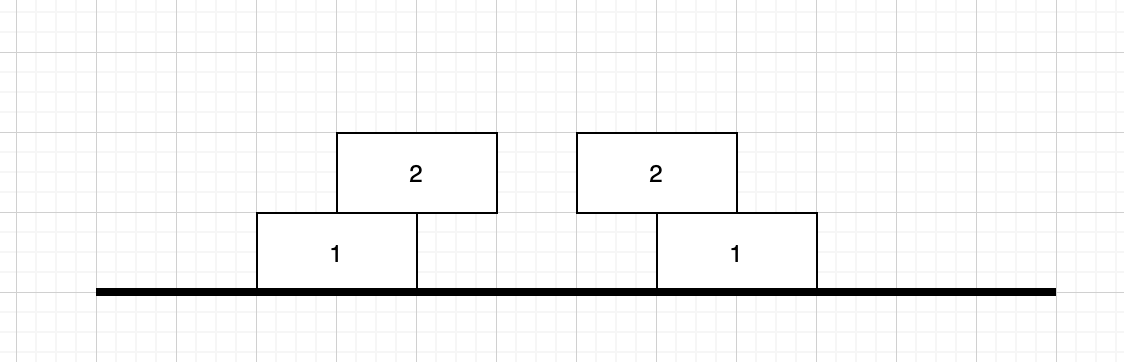
image.png
矩阵宽度 代表长度为2的积木放在k的场地上有几种放法
矩阵长度 代表有几个积木
d[i][j]代表第i个积木放在j位置有几种 需要二维数组，因为需要i-1和j-1
表格【假设k = 4，n = 4】
初始化

含义 1个积木
当上个积木位置是[0,1]此位置有几种放法 1
当上个积木位置是[1,2]此位置有几种放法 1
当上个积木位置是[2,3]此位置有几种放法 1

状态转移递推

2个积木 3个积木 4个积木 5个积木
1 2 2 4
2 2 4 4
1 2 2 4

状态转移方程
当 j+1 < k的时候，即可以放在➡️上角时候，dp[i][j] += dp[i-1][j+1]
当 j > 0 的时候，即可以放在⬅️上角时候，dp[i][j] += dp[i-1][j-1]
当 0 < j < k-1 时 ⬅️上角 和 ➡️上角都可以放置 dp[i][j] += (dp[i-1][j+1] + dp[i-1][j-1])
当5个积木时，放在[0,1]位置有4种放法，放在[1,2]位置有4种放法，放在[2,3]位置有4种放法。

  1. static int MOD = 998244353;
  2. public static void main(String[] args) {
  3.     Scanner scanner = new Scanner(System.in);
  4.     int n = scanner.nextInt();
  5.     int k = scanner.nextInt();
  6.     // dp[i][j]表示将第i个积木放在起始位置为j的位置有多少种摆法
  7.     // 状态转移也很好想，因为当前积木要么放在前一个积木的前上方
  8.     // 要么放在前一个积木的后上方，注意边界情况
  9.     long[][] dp = new long[n+1][k-1];
  10.     long ans = 0;
  11.     Arrays.fill(dp[1],1);
  12.     System.out.println("初始化dp = "+ Arrays.deepToString(dp));
  13.     for(int i = 2;i <= n;i++){
  14.         for(int j = 0;j < k - 1;j++){
  15.             if(j  > 0){
  16.                 dp[i][j] = dp[i-1][j-1];
  17.                 dp[i][j] %= MOD;
  18.             }
  19.             if(j + 1 < k - 1){
  20.                 dp[i][j] = dp[i-1][j+1];
  21.                 dp[i][j] %= MOD;
  22.             }
  23.             if (j > 0 && (j + 1 < k - 1)){
  24.                 dp[i][j] = (dp[i-1][j+1] + dp[i-1][j-1]);
  25.                 dp[i][j] %= MOD;
  26.             }
  27.         }
  28.     }
  29.     System.out.println("dp = "+ Arrays.deepToString(dp));
  30.     for(int i = 0;i < k-1;i++){
  31.         ans = (ans + dp[n][i])%MOD;
  32.     }
  33.     System.out.println(ans);
  34. }

Case 3

给定一个正整数 n ，将其拆分为 k 个 正整数 的和（ k >= 2 ），并使这些整数的乘积最大化。 返回 你可以获得的最大乘积 。

确定递推公式
可以想 dp[i]最大乘积是怎么得到的呢？
其实可以从1遍历j，然后有两种渠道得到dp[i].

  • 一个是j * (i - j) 直接相乘。
  • 一个是j * dp[i - j]，相当于是拆分(i - j)
    1. public int integerBreak(int n) {
    2.   int[] dp = new int[n+1];
    3.   dp[1] = 1;
    4.   for(int i = 2;i <= n;i++){
    5.       for(int j = 1;j < i;j ++){
    6.           dp[i] = Math.max(dp[i],j*(i-j));
    7.           dp[i] = Math.max(dp[i],dp[j]*(i-j));
    8.       }
    9.   }
    10.   return dp[n];
    11. }

    Case 3 对角线式动态规划

    给你一个字符串 s ，请你统计并返回这个字符串中 回文子串 的数目。回文字符串 是正着读和倒过来读一样的字符串。子字符串 是字符串中的由连续字符组成的一个序列。具有不同开始位置或结束位置的子串，即使是由相同的字符组成，也会被视作不同的子串。 示例 1： 输入：s = “abc” 输出：3 解释：三个回文子串: “a”, “b”, “c” 示例 2： 输入：s = “aaa” 输出：6 解释：6个回文子串: “a”, “a”, “a”, “aa”, “aa”, “aaa”

递推分析

举例 “aba”
转移方程
初始化 a,b,c都为回文
为了兼容”aa”和”aba”这种情况,需设置i-j >= 2的限制,返回为true
dp数组呈现对角线以上是边界范围，1行3列代表从’a’到’c’即”abc”的子串是否符合，此时两个条件’a’ == ‘c’ 相等并且 前一个状态2行2列的 “b” 需要是回文子串。

a 1 b 2 c 3
a 1 true false true
b 2
true false
c 3

true 
  1. public int countSubstrings(String s) {
  2.         int n = s.length();
  3.         int max = 0;
  4.         boolean[][] dp = new boolean[n+1][n+1];
  5.         System.out.println("初始化dp ");
  6.         for (int i = 1; i <= n; i++) {
  7.             dp[i][i] = true;
  8.         }
  9.         System.out.println(Arrays.deepToString(dp));
  10.         System.out.println("最终dp ");
  11.         for (int i = n; i >= 1; i--) {
  12.             for (int j = i+1; j <= n; j++) {
  13.                 if (s.charAt(i-1) == s.charAt(j-1)){
  14.                     if (dp[i+1][j-1] || j-i <= 2){
  15.                         dp[i][j] = true;
  16.                     }
  17.                 }
  18.             }
  19.         }
  20.         System.out.println(Arrays.deepToString(dp));
  21.         for (int i = 1; i <= n; i++) {
  22.             for (int j = i; j <= n; j++) {
  23.                 if (dp[i][j]){
  24.                     max += 1;
  25.                 }
  26.             }
  27.         }
  28.         return max;
  29.  }