单调栈算法技巧整理

单调栈算法，可以维持栈内保持单调递增或者递减，不符合的弹出栈进行处理，局部最大值可知。

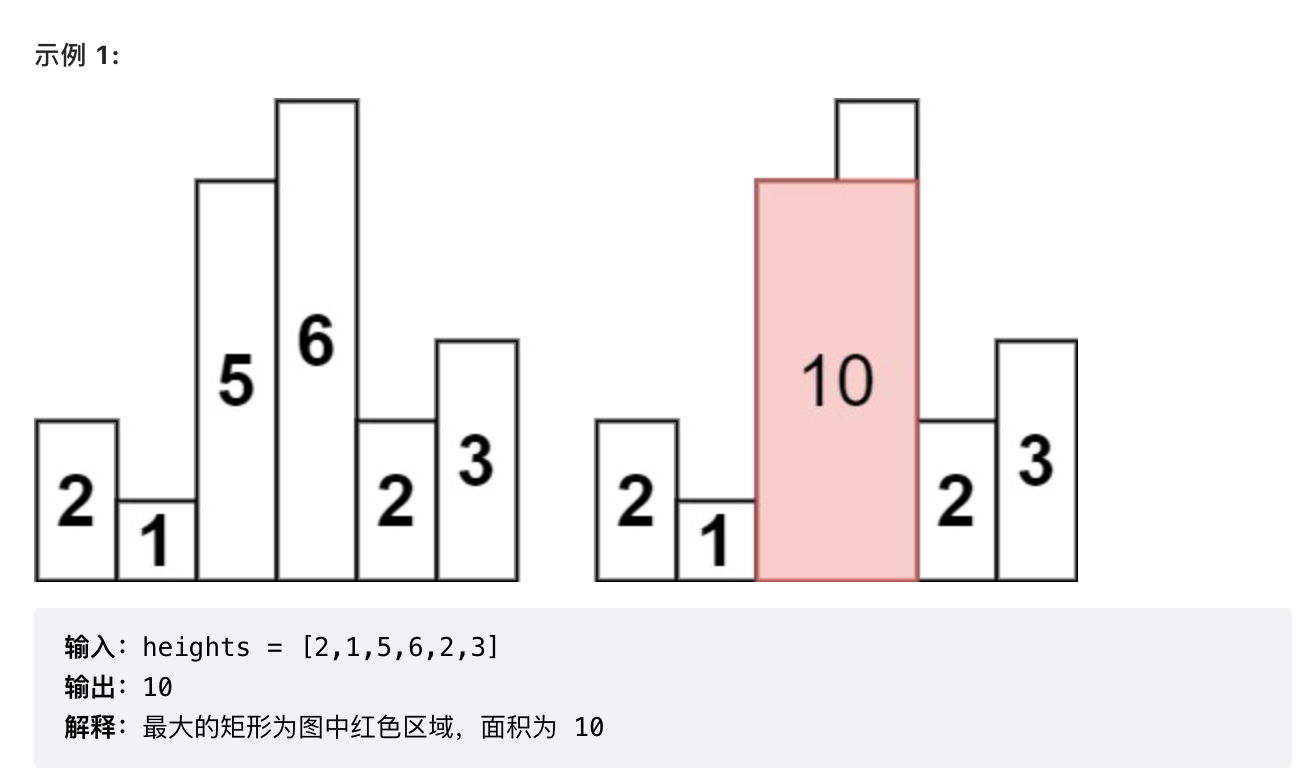
例子 1 最大矩形 【根据概念-边界补零】

细节

1.已知结论 第i个矩形面积最大时出现在左右两边第1个小于其高度的矩形围成的面积。【符合单调栈的特性】
2.因为是遇到小的才弹出，所以前后要设置最小值，需要前一个和后一个，所以第一个和最后一个需要满足通式，因此前后个补了0.

class Solution {
    public int largestRectangleArea(int[] heights) {
        int len = heights.length;
        Stack<Integer> stack = new Stack<>();
        int[] arr = new int[len+2];
        System.arraycopy(heights,0,arr,1,heights.length);
        int res = 0;
        for(int i = 0;i < len+2;i ++){
            while(!stack.isEmpty() && arr[stack.peek()] > arr[i]){
                int pop = stack.pop();
                if(stack.isEmpty()) break;
                int l = stack.peek();
                int c = i - l - 1;
                int k = arr[pop];
                res = Math.max(res,c*k);
            }
            stack.push(i);
        }
        return res;
    }
}

例子2 接雨水

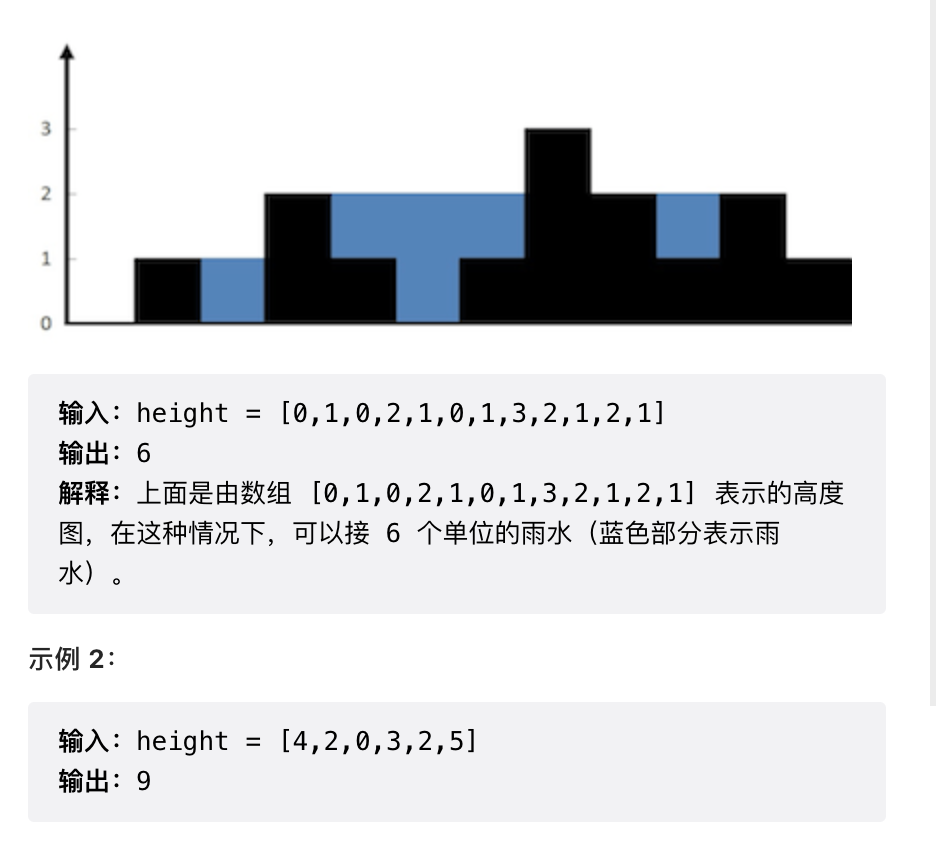
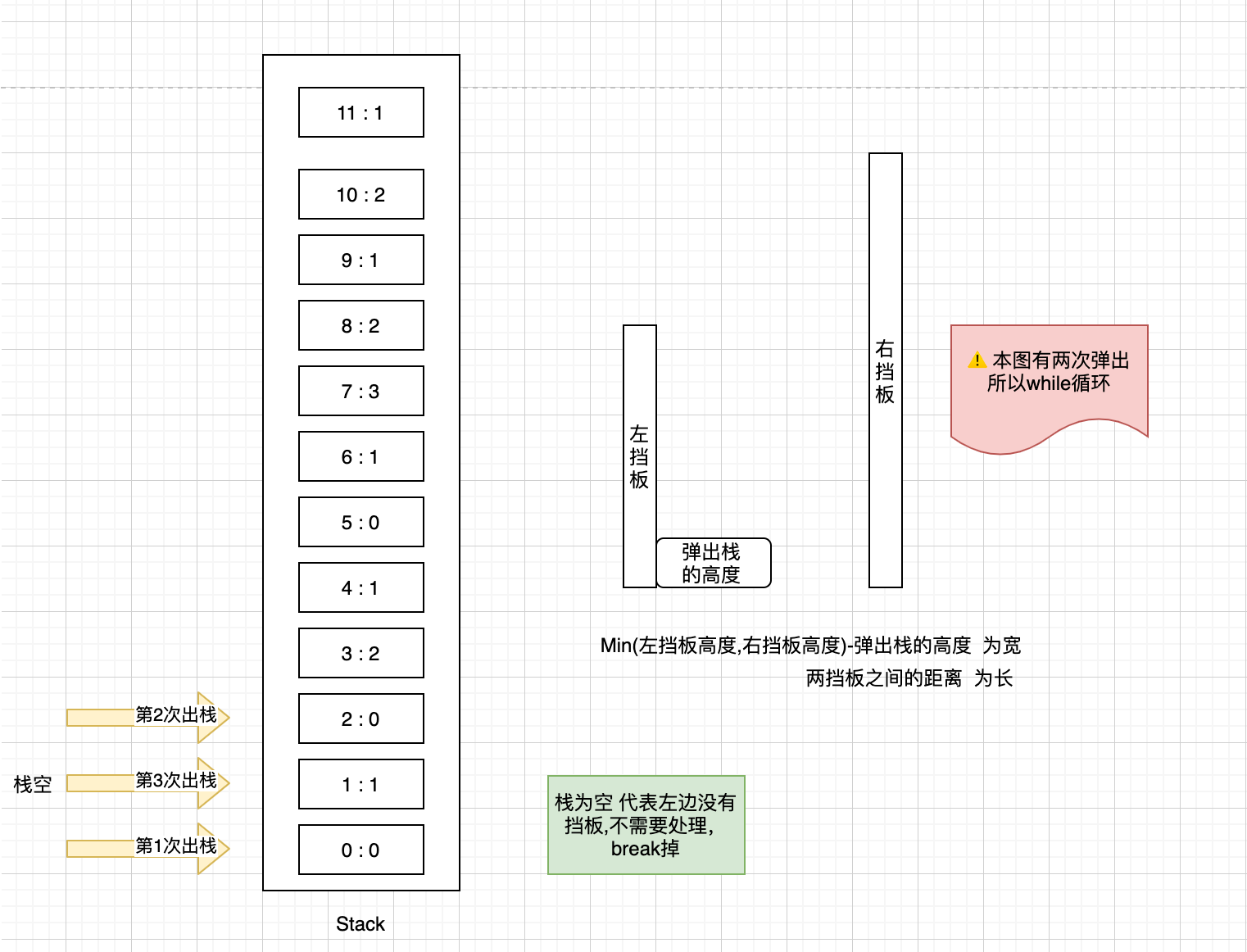
class Solution {
    public int trap(int[] height) {
        int len = height.length;
        LinkedList<Integer> stack = new LinkedList<>();
        int count = 0;
        for(int i = 0;i < len;i ++){
            while(!stack.isEmpty() && height[stack.peek()] < height[i]){
                int pop = stack.pop();
                if(stack.isEmpty()) break;
                int l = stack.peek();
                int c = i - l - 1;
                int k = Math.min(height[l],height[i]);
                count += c * (k - height[pop]);
            }
            stack.push(i);
            System.out.println(stack);
        }
        return count;
    }
}