动态规划( dynamic programming, DP )是一种将复杂问题分解成更小的子问题来解决的优
化技术。
注意,动态规划和分而治之是不同的方法。 分而治之方法是把问题分解成相互独立的子问题,然后组合它们的答案, 而动态规划则是将问题分解成相互依赖的子问题。
用动态规划解决问题时,要遵循三个重要步骤:
(1) 定义子问题;
(2) 实现要反复执行来解决子问题的部分( 这一步要参考前一节讨论的递归的步骤);
(3) 识别并求解出基线条件。
能用动态规划解决的一些著名问题如下。
- 背包问题:给出一组项,各自有值和容量,目标是找出总值最大的项的集合。这个问题的限制是,总容量必须小于等于“背包”的容量。
- 最长公共子序列:找出一组序列的最长公共子序列(可由另一序列删除元素但不改变余下元素的顺序而得到)。
- 矩阵链相乘:给出一-系列矩阵,目标是找到这些矩阵相乘的最高效办法( 计算次数尽可能少)。相乘运算不会进行,解决方案是找到这些矩阵各自相乘的顺序。
- 硬币找零:给出面额为d, … ,
的一定数量的硬币和要找零的钱数,找出有多少种找零的方法。
- 图的全源最短路径: 修路问题 Floyd-Warshall算法
背包问题
问题描述
与一个背包,容量为4,现有以下物品
| 物品 | 重量 | 价格 |
|---|---|---|
| 吉他(G) | 1 | 1500 |
| 音响(S) | 4 | 3000 |
| 电脑(L ) | 3 | 2000 |
- 要求达到的目标为装入的背包的总价值最大,并且重量不超出
- 要求装入的物品不能重复
思路分析和图解
算法的主要思想, 利用动态规划来解决。每次遍历到的第i个物品,根据w[i]和v[i]来确定是否需要将该物品放入背包中。即对于给定的n个物品,设v[i]、 w[i]分别为第i个物品的价值和重量,C为背包的容量。再令v[i][j]表示在前i个物品中能够装入容量为j的背包中的最大价值。则我们有下面的结果:
| 物品i / 容量j | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | |
| 吉他(G) | 0 | 1500G | 1500G | 1500G | 1500G |
| 音响(S) | 0 | 1500G | 1500G | 1500G | 3000S |
| 电脑(L ) | 0 | 1500G | 1500G | 2000L | 2000L+1500G |
- v[i][0] = v[0][j] // 表示填入表的第一行第一列是0
- 当w[i] > j 时; v[i][j] = v[i-1][j] // 当准备加入新增的商品容量大于当前背包的容量时,就直接使用上一个单元格的装入策略
- 当j>=w[i]时; v[i][j] = max(v[i-1][j] , v[i]+v[i-1][j-w[i]])
// 当准备加入新增的商品容量不大于当前背包的容量时,
// 装入的方式:
- v[i-1][j] 上一个单元格装入的最大值
- v[i] 当前商品的价值
- v[i-1][j-w[i]] 装入 i-1商品,搭配剩余空间j-w[i]的最大值
代码实现
function getMaxValOnDiffGoods(map, j) {const w = [], val = [], v = []v.push(new Array(j + 1))for(item of map.values()) {w.push(item[0]);val.push(item[1])v.push(new Array(j + 1))}for (let i = 0; i < v.length; i++) {v[i][0] = 0}for (let i = 0; i < v[0].length; i++) {v[0][i] = 0}const path = new Array(v[0].length) // 用来记录存放的是什么东西for (let i = 0; i < v[0].length; i++) {path[i] = new Array(j + 1)}// 根据背包公示来动态规划处理for (let i = 1; i < v.length; i++) {for (let j = 1; j < v[i].length; j++) {if (w[i - 1] > j) {v[i][j] = v[i-1][j]} else {// v[i][j] = Math.max(v[i-1][j] ,val[i - 1] + v[i-1][j-w[i-1]])if (v[i-1][j] < val[i - 1] + v[i-1][j-w[i-1]] ) {v[i][j] = val[i - 1] + v[i-1][j-w[i-1]]path[i][j] = 1} else {v[i][j] = v[i-1][j]}}}}console.log(v)let x = path.length - 1let y = path[0].length - 1const goods = [...map.keys()]while(x > 0 && y > 0) {if (path[x][y] === 1) {console.log(`${goods[x-1]}放入背包`)y = y - w[x - 1]}x--}}var map = new Map()map.set('G', [1, 1500])map.set('S', [4, 3000])map.set('L', [3, 2000])console.log(getMaxValOnDiffGoods(map, 4))
爬楼梯问题
有n级台阶,一个人每次上一级或者两级,问有多少种走完n级台阶的方法
| 台阶数 | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| 走一步或两步 | 0 | 1 | 2 | 3 | 5 |
当n为1时,f(n) = 1,
当n为2时,f(n) =2,
就是说当台阶只有一级的时候,方法数是一种,台阶有两级的时候,方法数为2。
那么当我们要走上n级台阶,必然是从n-1级台阶迈一步或者是从n-2级台阶迈两步,所以到达n级台阶的方法数必然是到达n-1级台阶的方法数加上到达n-2级台阶的方法数之和。即f(n) = f(n-1)+f(n-2)。
function climbStairs (n) {if (n < 1) return '台阶不能小于1';if (n === 1) return 1;if (n === 2) return 2;const arr = [1, 2]for(let i = 2; i < n; i++) {arr[i] = arr[i - 1] + arr[i - 2]}return arr[n-1];};console.log(climbStairs(5))
最小硬币找零
最长公共子序列
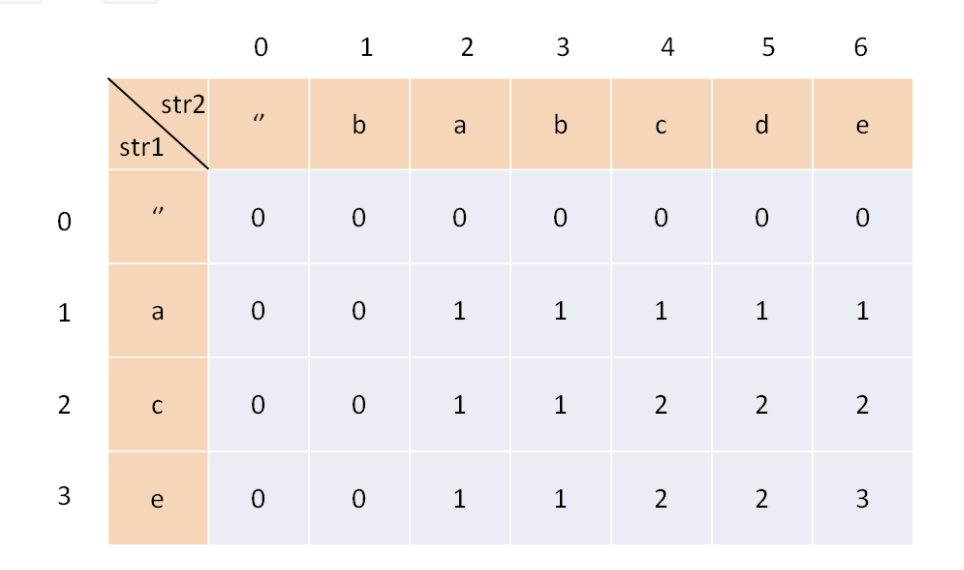
// 暴力破解function findMaxSeq(text1, text2) {function dp (i, j) {if(i === -1 || j === -1) {return 0}if(text1[i] === text2[j]) {return dp(i - 1, j - 1) + 1}return Math.max(dp(i-1, j), dp(i, j-1))}return dp(text1.length - 1, text2.length - 1)}// console.log(findMaxSeq('abcde', 'ade'))console.log(findMaxSeq('babcdey', 'aczex'))// 最长公共子序列function findMaxSubStr(str1, str2) {// 容错const chess = Array.from({length: str1.length + 1},() => Array.from({length: str2.length + 1},() => 0),);for(let i = 1; i<= str1.length; i++) {for(let j = 1; j<= str2.length; j++) {chess[i][j] = Math.max(chess[i-1][j], chess[i][j-1]) + Number(str1[i] === str2[j])}}// console.log(chess);return chess[str1.length][str2.length];}console.log(findMaxSubStr('ace', 'babcde'))
矩阵链相乘
修路问题 Floyd-Warshall算法


