学习JavaScript数据结构与算法（第3版）@www.java1234.com.pdf

栈

我们知道，可以在数组的任意位置上删除或添加元素。然而，有时候还需要一种能在添加或删除元素时进行
更多控制的数据结构。有两种类似于数组的数据结构在添加和删除元素时更为可控，它们就是栈和队列。

栈是一种遵从后进先出( LIFO)原则的有序集合。新添加或待删除的元素都保存在栈的同
一端，称作栈顶，另一端就叫栈底。在栈里，新元素都靠近栈顶，旧元素都接近栈底。

在现实生活中也能发现很多栈的例子。例如，一摞书或者餐厅里叠放的盘子。
栈也被用在编程语言的编译器和内存中保存变量、方法调用等，也被用于浏览器历史记录
(浏览器的返回按钮)。

栈的简易实现

// 最简单大 栈数据结构 实现
class Stack {
  constructor() {
    this.count = 0;
    this.items = {};
  }
  push(element) {
    this.items[this.count] = element;
    this.count++;
  }
  pop() {
    if (this.isEmpty()) {
      return undefined;
    }
    this.count--;
    const result = this.items[this.count];
    delete this.items[this.count];
    return result;
  }
  peek() {
    if (this.isEmpty()) {
      return undefined;
    }
    return this.items[this.count - 1];
  }
  isEmpty() {
    return this.count === 0;
  }
  size() {
    return this.count;
  }
  clear() {
    /* while (!this.isEmpty()) {
        this.pop();
      } */
    this.items = {};
    this.count = 0;
  }
  toString() {
    if (this.isEmpty()) {
      return '';
    }
    let objString = `${this.items[0]}`;
    for (let i = 1; i < this.count; i++) {
      objString = `${objString},${this.items[i]}`;
    }
    return objString;
  }
}

如何保护数据结构内部元素？

下划线命令约定
用ES2015的限定作用域Symbol
使用ES2015的WeakMap实现类
ECMAScript 类私有属性提案 “#“
用途

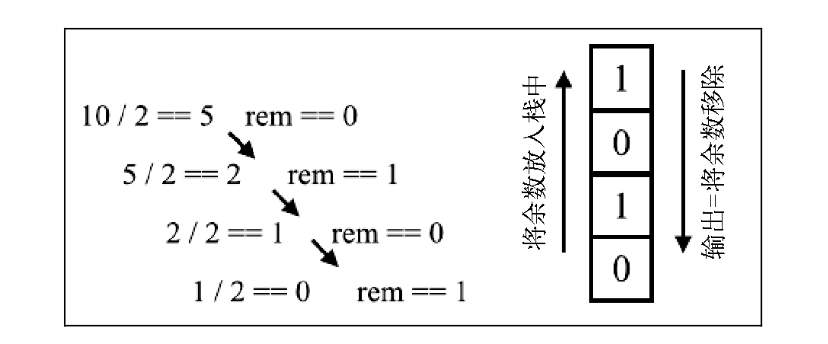
从十进制到二进制

计算器实现（中缀、前缀、后缀表达式）

队列
队列和栈非常类似，但是使用了与后进先出不同的原则。
队列是遵循先进先出(FIFO,也称为先来先服务)原则的一~组有序的项。队列在尾部添加新
元素，并从顶部移除元素。最新添加的元素必须排在队列的末尾。

队列的简易实现
```javascript class Deque { constructor() { this.count = 0; this.lowestCount = 0; this.items = {}; }

addFront(element) { if (this.isEmpty()) { this.addBack(element); } else if (this.lowestCount > 0) { this.lowestCount—; this.items[this.lowestCount] = element; } else { for (let i = this.count; i > 0; i—) {
```
 this.items[i] = this.items[i - 1];
```
} this.count++; this.items[0] = element; } }

addBack(element) { this.items[this.count] = element; this.count++; }

removeFront() { if (this.isEmpty()) { return undefined; } const result = this.items[this.lowestCount]; delete this.items[this.lowestCount]; this.lowestCount++; return result; }

removeBack() { if (this.isEmpty()) { return undefined; } this.count—; const result = this.items[this.count]; delete this.items[this.count]; return result; }

peekFront() { if (this.isEmpty()) { return undefined; } return this.items[this.lowestCount]; }

peekBack() { if (this.isEmpty()) { return undefined; } return this.items[this.count - 1]; }

isEmpty() { return this.size() === 0; }

clear() { this.items = {}; this.count = 0; this.lowestCount = 0; }

size() { return this.count - this.lowestCount; }

toString() { if (this.isEmpty()) { return ‘’; } let objString = ${this.items[this.lowestCount]}; for (let i = this.lowestCount + 1; i < this.count; i++) { objString = ${objString},${this.items[i]}; } return objString; } }

<a name="QJr8K"></a>
## 双端队列
双端队列(deque,或称double- ended queue)是一种种允许我们同时从前端和后端添加和移除<br />元素的特殊队列。<br />双端队列在现实生活中的例子有电影院、餐厅中排队的队伍等。举个例子，一个刚买了票的<br />人如果，只是还需要再问-些简单的信息，就可以直接回到队伍的头部。另外，在队伍末尾的人如<br />果赶时间，他可以直接离开队伍。<br />在计算机科学中，双端队列的一个常见应用是存储- - 系列的撤销操作。每当用户在软件中进<br />行了一个操作，该操作会被存在一个双端队列中( 就像在一个栈里)。当用户点击撤销按钮时,<br />该操作会被从双端队列中弹出,表示它被从后面移除了。在进行了预先定义的---定数量的操作后，<br />最先进行的操作会被从双端队列的前端移除。由于双端队列同时遵守了先进先出和后进先出原<br />则，可以说它是把队列和栈相结合的一种数据结构。
<a name="uRcgY"></a>
## 队列和双端队列的应用
- 循环队列一击 鼓传花游戏
- 回文检查器 （回文例子：madam）
- javascript任务队列
<a name="qv46m"></a>
# 链表
要存储多个元素，数组(或列表)可能是最常用的数据结构。正如本书之前提到的，每种语言都实现了数组。这种数据结构非常方便，提供了一个便利的[]语法来访问其元素。然而，这种数据结构有一个缺点: (在大多数语言中)数组的大小是固定的，从数组的起点或中间插入或移除项的成本很高，因为需要移动元素。( 尽管我们已经学过，JavaScript 有来自Array 类的方法可以帮我们做这些事，但背后的情况同样如此。)<br />链表存储有序的元素集合,但不同于数组，链表中的元素在内存中并不是连续放置的。每个<br />元素由一个存储元素本身的节点和一一个指向下一一个元素的引用(也称指针或链接)组成。下图展<br />示了一个链表的结构。<br />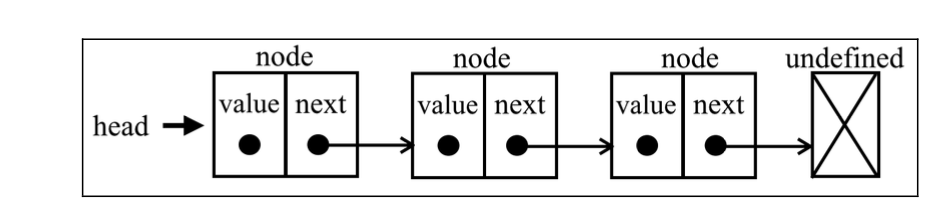![image.png](https://cdn.nlark.com/yuque/0/2020/png/190178/1590933054487-6902f10e-2b03-4132-9f48-d97bade50bbb.png#align=left&display=inline&height=105&margin=%5Bobject%20Object%5D&name=image.png&originHeight=210&originWidth=946&size=43327&status=done&style=none&width=473)
现实中的例子： 康加舞队、寻宝游戏、火车
<a name="OxPSs"></a>
## 链表的简易实现
```javascript
class LinkedList {
  constructor(equalsFn = (a, b) => a === b) {
    this.equalsFn = equalsFn;
    this.count = 0;
    this.head = undefined;
  }
  push(element) {
    const node = new Node(element);
    let current;
    if (this.head == null) {
      // catches null && undefined
      this.head = node;
    } else {
      current = this.head;
      while (current.next != null) {
        current = current.next;
      }
      current.next = node;
    }
    this.count++;
  }
  getElementAt(index) {
    if (index >= 0 && index <= this.count) {
      let node = this.head;
      for (let i = 0; i < index && node != null; i++) {
        node = node.next;
      }
      return node;
    }
    return undefined;
  }
  insert(element, index) {
    if (index >= 0 && index <= this.count) {
      const node = new Node(element);
      if (index === 0) {
        const current = this.head;
        node.next = current;
        this.head = node;
      } else {
        const previous = this.getElementAt(index - 1);
        node.next = previous.next;
        previous.next = node;
      }
      this.count++;
      return true;
    }
    return false;
  }
  removeAt(index) {
    if (index >= 0 && index < this.count) {
      let current = this.head;
      if (index === 0) {
        this.head = current.next;
      } else {
        const previous = this.getElementAt(index - 1);
        current = previous.next;
        previous.next = current.next;
      }
      this.count--;
      return current.element;
    }
    return undefined;
  }
  remove(element) {
    const index = this.indexOf(element);
    return this.removeAt(index);
  }
  indexOf(element) {
    let current = this.head;
    for (let i = 0; i < this.size() && current != null; i++) {
      if (this.equalsFn(element, current.element)) {
        return i;
      }
      current = current.next;
    }
    return -1;
  }
  isEmpty() {
    return this.size() === 0;
  }
  size() {
    return this.count;
  }
  getHead() {
    return this.head;
  }
  clear() {
    this.head = undefined;
    this.count = 0;
  }
  toString() {
    if (this.head == null) {
      return '';
    }
    let objString = `${this.head.element}`;
    let current = this.head.next;
    for (let i = 1; i < this.size() && current != null; i++) {
      objString = `${objString},${current.element}`;
      current = current.next;
    }
    return objString;
  }
}
class Node {
  constructor(element, next) {
    this.element = element;
    this.next = next;
  }
}

链表的变体

双向链表
循环链表
有序链表

StackLinkedList类

集合

集合是由一组无序且唯一(即不能重复)的项组成的。该数据结构使用了与有限集合相同的数学概念，但应用在计算机科学的数据结构中。
集合的运算：并集、交集、差集、子集

集合的简易实现

class Set {
constructor() {
  this.items = {};
}
add(element) {
  if (!this.has(element)) {
    this.items[element] = element;
    return true;
  }
  return false;
}
delete(element) {
  if (this.has(element)) {
    delete this.items[element];
    return true;
  }
  return false;
}
has(element) {
  return Object.prototype.hasOwnProperty.call(this.items, element);
}
values() {
  return Object.values(this.items);
}
union(otherSet) {
  const unionSet = new Set();
  this.values().forEach(value => unionSet.add(value));
  otherSet.values().forEach(value => unionSet.add(value));
  return unionSet;
}
intersection(otherSet) {
  const intersectionSet = new Set();
  const values = this.values();
  const otherValues = otherSet.values();
  let biggerSet = values;
  let smallerSet = otherValues;
  if (otherValues.length - values.length > 0) {
    biggerSet = otherValues;
    smallerSet = values;
  }
  smallerSet.forEach(value => {
    if (biggerSet.includes(value)) {
      intersectionSet.add(value);
    }
  });
  return intersectionSet;
}
difference(otherSet) {
  const differenceSet = new Set();
  this.values().forEach(value => {
    if (!otherSet.has(value)) {
      differenceSet.add(value);
    }
  });
  return differenceSet;
}
isSubsetOf(otherSet) {
  if (this.size() > otherSet.size()) {
    return false;
  }
  let isSubset = true;
  this.values().every(value => {
    if (!otherSet.has(value)) {
      isSubset = false;
      return false;
    }
    return true;
  });
  return isSubset;
}
isEmpty() {
  return this.size() === 0;
}
size() {
  return Object.keys(this.items).length;
}
clear() {
  this.items = {};
}
toString() {
  if (this.isEmpty()) {
    return '';
  }
  const values = this.values();
  let objString = `${values[0]}`;
  for (let i = 1; i < values.length; i++) {
    objString = `${objString},${values[i].toString()}`;
  }
  return objString;
}
}

应用

在数学中,有一个叫作多重集的概念，它允许我们向集合中插入之前已经添加过的元素。多重集(或袋)在计算集合中元素的出现次数时很有用。它也在数据库系统中得到了广泛运用。

字典和散列表

集合表示一组互不相同的元素(不重复的元素)。在字典中，存储的是[键,值]对，其中键名是用来查询特定元素的。字典和集合很相似，集合以[值，值]的形式存储元素,字典则是以[键，值]的形式来存储元素。字典也称作映射、符号表或关联数组。在计算机科学中，字典经常用来保存对象的引用地址。例如，打开Chrome |开发者工具中的Memory标签页，执行快照功能，我们就能看到内存中的一些对象和它们对应的地址引用

字典类的简易实现

class Dictionary {
  constructor(toStrFn = defaultToString) {
    this.toStrFn = toStrFn;
    this.table = {};
  }
  set(key, value) {
    if (key != null && value != null) {
      const tableKey = this.toStrFn(key);
      this.table[tableKey] = new ValuePair(key, value);
      return true;
    }
    return false;
  }
  get(key) {
    const valuePair = this.table[this.toStrFn(key)];
    return valuePair == null ? undefined : valuePair.value;
  }
  hasKey(key) {
    return this.table[this.toStrFn(key)] != null;
  }
  remove(key) {
    if (this.hasKey(key)) {
      delete this.table[this.toStrFn(key)];
      return true;
    }
    return false;
  }
  values() {
    return this.keyValues().map(valuePair => valuePair.value);
  }
  keys() {
    return this.keyValues().map(valuePair => valuePair.key);
  }
  keyValues() {
    return Object.values(this.table);
  }
  forEach(callbackFn) {
    const valuePairs = this.keyValues();
    for (let i = 0; i < valuePairs.length; i++) {
      const result = callbackFn(valuePairs[i].key, valuePairs[i].value);
      if (result === false) {
        break;
      }
    }
  }
  isEmpty() {
    return this.size() === 0;
  }
  size() {
    return Object.keys(this.table).length;
  }
  clear() {
    this.table = {};
  }
  toString() {
    if (this.isEmpty()) {
      return '';
    }
    const valuePairs = this.keyValues();
    let objString = `${valuePairs[0].toString()}`;
    for (let i = 1; i < valuePairs.length; i++) {
      objString = `${objString},${valuePairs[i].toString()}`;
    }
    return objString;
  }
}
function defaultToString(item) {
  if (item === null) {
    return 'NULL';
  } else if (item === undefined) {
    return 'UNDEFINED';
  } else if (typeof item === 'string' || item instanceof String) {
    return `${item}`;
  }
  return item.toString();
}
class ValuePair {
  constructor(key, value) {
    this.key = key;
    this.value = value;
  }
  toString() {
    return `[#${this.key}: ${this.value}]`;
  }
}

散列表（也称作HashMap、HashTable)

散列算法的作用是尽可能快地在数据结构中找到一个值。在之前的章节中，你已经知道如果
要在数据结构中获得一个值 (使用get方法),需要迭代整个数据结构来找到它。如果使用散列函数，就知道值的具体位置，因此能够快速检索到该值。散列函数的作用是给定一个键值，然后返回值在表中的地址。
散列表有一些在计算机科学中应用的例子。因为它是字典的一种实现，所以可以用作关联数组。它也可以用来对数据库进行索引。当我们在关系型数据库(如MySQL、Microsoft SQL Server、Oracle，等等)中创建一个新的表时，一个不错的做法是同时创建一个索引来更快地查询到记录的key。在这种情况下，散列表可以用来保存键和对表中记录的引用。另一个很常见的应用是使用散列表来表示对象。JavaScript语言内部就是使用散列表来表示每个对象。此时，对象的每个属性和方法(成员)被存储为key对象类型，每个key指向对应的对象成员。
继续以前一节中使用的电子邮件地址簿为例。我们将使用最常见的散列函数—lose lose散列函数，方法是简单地将每个键值中的每个字母的ASCII值相加，如下图所示。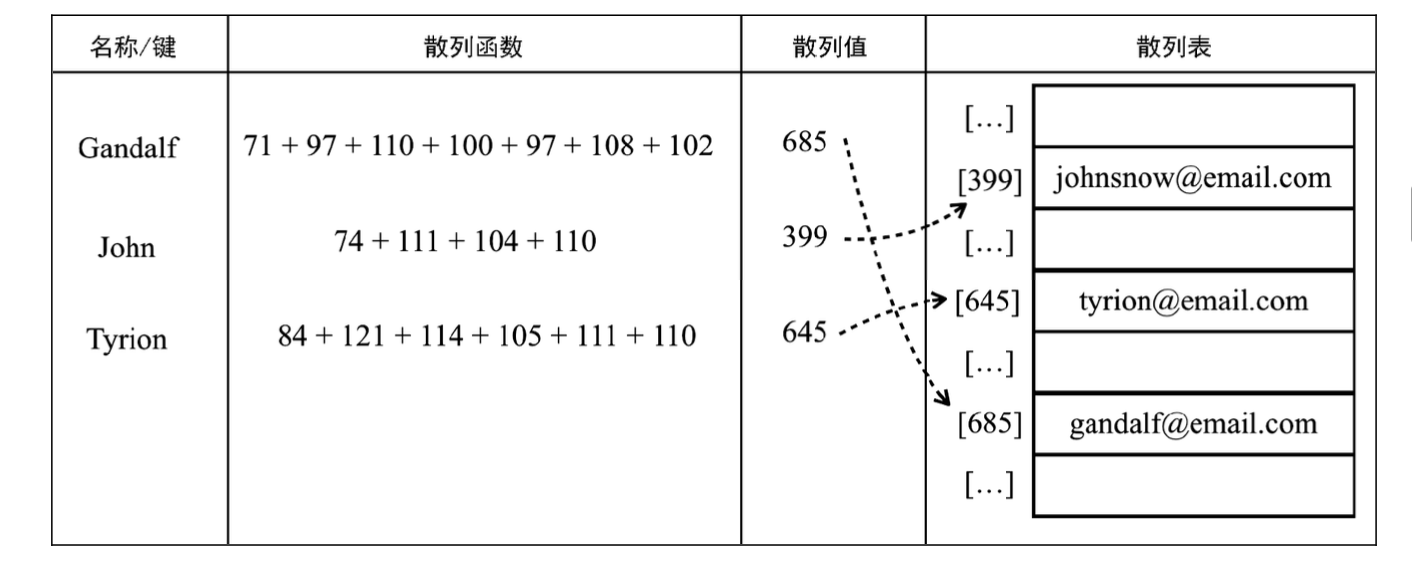

散列表的简易实现

class HashTable {
  constructor(toStrFn = defaultToString) {
    this.toStrFn = toStrFn;
    this.table = {};
  }
  loseloseHashCode(key) {
    if (typeof key === 'number') {
      return key;
    }
    const tableKey = this.toStrFn(key);
    let hash = 0;
    for (let i = 0; i < tableKey.length; i++) {
      hash += tableKey.charCodeAt(i);
    }
    return hash % 37;
  }
  /* djb2HashCode(key) {
    const tableKey = this.toStrFn(key);
    let hash = 5381;
    for (let i = 0; i < tableKey.length; i++) {
      hash = (hash * 33) + tableKey.charCodeAt(i);
    }
    return hash % 1013;
  } */
  hashCode(key) {
    return this.loseloseHashCode(key);
  }
  put(key, value) {
    if (key != null && value != null) {
      const position = this.hashCode(key);
      this.table[position] = new ValuePair(key, value);
      return true;
    }
    return false;
  }
  get(key) {
    const valuePair = this.table[this.hashCode(key)];
    return valuePair == null ? undefined : valuePair.value;
  }
  remove(key) {
    const hash = this.hashCode(key);
    const valuePair = this.table[hash];
    if (valuePair != null) {
      delete this.table[hash];
      return true;
    }
    return false;
  }
  getTable() {
    return this.table;
  }
  isEmpty() {
    return this.size() === 0;
  }
  size() {
    return Object.keys(this.table).length;
  }
  clear() {
    this.table = {};
  }
  toString() {
    if (this.isEmpty()) {
      return '';
    }
    const keys = Object.keys(this.table);
    let objString = `{${keys[0]} => ${this.table[keys[0]].toString()}}`;
    for (let i = 1; i < keys.length; i++) {
      objString = `${objString},{${keys[i]} => ${this.table[keys[i]].toString()}}`;
    }
    return objString;
  }
}
function defaultToString(item) {
  if (item === null) {
    return 'NULL';
  } else if (item === undefined) {
    return 'UNDEFINED';
  } else if (typeof item === 'string' || item instanceof String) {
    return `${item}`;
  }
  return item.toString();
}
class ValuePair {
  constructor(key, value) {
    this.key = key;
    this.value = value;
  }
  toString() {
    return `[#${this.key}: ${this.value}]`;
  }
}

处理散列表的冲突

分离链接
线性探查
双散列法

应用

在计算机科学中，字典经常用来保存对象的引用地址。例如，打开 Chrome | 开发者工具中的 Memory 标签页，执行快照功能，我们就能看到内存中的一些对象和它们对应的地址引用(用 @<数>表示)。
散列表应用
1. 对应数据库索引
2. 用散列表来表示对象
  树数据结构
  树是一种分层数据的抽象模型。现实生活中最常见的树的例子是家谱，或是公司的组织架构
  图，如下图所示。

二叉树和二叉搜索树（BST）

二叉搜索树简易实现

class BinarySearchTree {
  constructor(compareFn = (a, b) => a === b) {
    this.compareFn = compareFn;
    this.root = undefined;
  }
  insert(key) {
    // special case: first key
    if (this.root == null) {
      this.root = new Node(key);
    } else {
      this.insertNode(this.root, key);
    }
  }
  insertNode(node, key) {
    if (this.compareFn(key, node.key) === Compare.LESS_THAN) {
      if (node.left == null) {
        node.left = new Node(key);
      } else {
        this.insertNode(node.left, key);
      }
    } else if (node.right == null) {
      node.right = new Node(key);
    } else {
      this.insertNode(node.right, key);
    }
  }
  getRoot() {
    return this.root;
  }
  search(key) {
    return this.searchNode(this.root, key);
  }
  searchNode(node, key) {
    if (node == null) {
      return false;
    }
    if (this.compareFn(key, node.key) === Compare.LESS_THAN) {
      return this.searchNode(node.left, key);
    } else if (this.compareFn(key, node.key) === Compare.BIGGER_THAN) {
      return this.searchNode(node.right, key);
    }
    return true;
  }
  inOrderTraverse(callback) {
    this.inOrderTraverseNode(this.root, callback);
  }
  inOrderTraverseNode(node, callback) {
    if (node != null) {
      this.inOrderTraverseNode(node.left, callback);
      callback(node.key);
      this.inOrderTraverseNode(node.right, callback);
    }
  }
  preOrderTraverse(callback) {
    this.preOrderTraverseNode(this.root, callback);
  }
  preOrderTraverseNode(node, callback) {
    if (node != null) {
      callback(node.key);
      this.preOrderTraverseNode(node.left, callback);
      this.preOrderTraverseNode(node.right, callback);
    }
  }
  postOrderTraverse(callback) {
    this.postOrderTraverseNode(this.root, callback);
  }
  postOrderTraverseNode(node, callback) {
    if (node != null) {
      this.postOrderTraverseNode(node.left, callback);
      this.postOrderTraverseNode(node.right, callback);
      callback(node.key);
    }
  }
  min() {
    return this.minNode(this.root);
  }
  minNode(node) {
    let current = node;
    while (current != null && current.left != null) {
      current = current.left;
    }
    return current;
  }
  max() {
    return this.maxNode(this.root);
  }
  maxNode(node) {
    let current = node;
    while (current != null && current.right != null) {
      current = current.right;
    }
    return current;
  }
  remove(key) {
    this.root = this.removeNode(this.root, key);
  }
  removeNode(node, key) {
    if (node == null) {
      return undefined;
    }
    if (this.compareFn(key, node.key) === Compare.LESS_THAN) {
      node.left = this.removeNode(node.left, key);
      return node;
    } else if (this.compareFn(key, node.key) === Compare.BIGGER_THAN) {
      node.right = this.removeNode(node.right, key);
      return node;
    }
    // key is equal to node.item
    // handle 3 special conditions
    // 1 - a leaf node
    // 2 - a node with only 1 child
    // 3 - a node with 2 children
    // case 1
    if (node.left == null && node.right == null) {
      node = undefined;
      return node;
    }
    // case 2
    if (node.left == null) {
      node = node.right;
      return node;
    } else if (node.right == null) {
      node = node.left;
      return node;
    }
    // case 3
    const aux = this.minNode(node.right);
    node.key = aux.key;
    node.right = this.removeNode(node.right, aux.key);
    return node;
  }
}
const Compare = {
  LESS_THAN: -1,
  BIGGER_THAN: 1,
  EQUALS: 0
};
class Node {
  constructor(key) {
    this.key = key;
    this.left = undefined;
    this.right = undefined;
  }
  toString() {
    return `${this.key}`;
  }
}

树的遍历

中序：排序
先序：打印结构化文档
后序：（计算一个目录及子目录所有文件所占大小）

自平衡树（AVL 与红黑树）

对AVL书插人和移除节点可能会造成旋转，所以我们需要一个包含多次插人和删除的自平衡树,红黑树是比较好的。如果插人和删除频率较低(我们更需要多次进行搜索操作), 那么AVL树比红黑树更好。

二叉堆（一种特殊的二叉树）

它是一棵完全二二叉树，表示树的每-层都有左侧和右侧子节点(除了最后一层的叶节点), 并且最后一层的叶节点尽可能都是左侧子节点，这叫作结构特性。
二叉堆不是最小堆就是最大堆。最小堆允许你快速导出树的最小值，最大堆允许你快速导出树的最大值。所有的节点都大于等于( 最大堆)或小于等于( 最小堆)每个它的子节点。这叫做堆特性
二叉最小堆的简易实现
```javascript class MinHeap { constructor(compareFn = (a, b) => a === b) { this.compareFn = compareFn; this.heap = []; } getLeftIndex(index) { return (2 index) + 1; } getRightIndex(index) { return (2 index) + 2; } getParentIndex(index) { if (index === 0) {
```
return undefined;
```
} return Math.floor((index - 1) / 2); } size() { return this.heap.length; } isEmpty() { return this.size() <= 0; } clear() { this.heap = []; } findMinimum() { return this.isEmpty() ? undefined : this.heap[0]; } insert(value) { if (value != null) {
```
const index = this.heap.length;
this.heap.push(value);
this.siftUp(index);
return true;
```
} return false; } siftDown(index) { let element = index; const left = this.getLeftIndex(index); const right = this.getRightIndex(index); const size = this.size(); if (
```
left < size &&
this.compareFn(this.heap[element], this.heap[left]) === Compare.BIGGER_THAN
```
) {
```
element = left;
```
} if (
```
right < size &&
this.compareFn(this.heap[element], this.heap[right]) === Compare.BIGGER_THAN
```
) {
```
element = right;
```
} if (index !== element) {
```
swap(this.heap, index, element);
this.siftDown(element);
```
} } siftUp(index) { let parent = this.getParentIndex(index); while (
```
index > 0 &&
this.compareFn(this.heap[parent], this.heap[index]) === Compare.BIGGER_THAN
```
) {
```
swap(this.heap, parent, index);
index = parent;
parent = this.getParentIndex(index);
```
} } extract() { if (this.isEmpty()) {
```
return undefined;
```
} if (this.size() === 1) {
```
return this.heap.shift();
```
} const removedValue = this.heap[0]; this.heap[0] = this.heap.pop(); this.siftDown(0); return removedValue; } heapify(array) { if (array) {
```
this.heap = array;
```
} const maxIndex = Math.floor(this.size() / 2) - 1; for (let i = 0; i <= maxIndex; i++) {
```
this.siftDown(i);
```
} return this.heap; } getAsArray() { return this.heap; } } class MaxHeap extends MinHeap { constructor(compareFn = defaultCompare) { super(compareFn); this.compareFn = compareFn; this.compareFn = reverseCompare(compareFn); } }

应用

堆排序
DOM, AST 等应用都是对人脑分层分类认知的建模, 都是树
文件压缩（霍夫曼树）
图

图的概念

顶点、边、有向图、无向图、加权图、无环图连通图

图的表示

邻接矩阵、邻接表、关联矩阵

创建Graph类

图的遍历

广度优先
深度优先

应用

最小生成树
1. Prim 算法对应现实生活中的修路问题
2. KrusKal算法对应现实用说中的公交站问题
最短路径算法
1. Dikstra算法（属于贪心算法）
2. Floyd-Warshall算法（属于动态规划算法）

JavaScript 数据结构算法设计模式与编程思想

javascript数据结构

栈

栈的简易实现

如何保护数据结构内部元素？

用途

队列

队列的简易实现

链表的变体

集合

集合的简易实现

应用

字典和散列表

字典类的简易实现

散列表（也称作HashMap、HashTable)

散列表的简易实现

处理散列表的冲突

应用

树数据结构

二叉搜索树简易实现

树的遍历

自平衡树（AVL 与红黑树）

二叉堆（一种特殊的二叉树）

二叉最小堆的简易实现

应用

图

创建Graph类

图的遍历

应用

javascript数据结构

栈

栈的简易实现

如何保护数据结构内部元素？

用途

队列

队列的简易实现

链表的变体

集合

集合的简易实现

应用

字典和散列表

字典类的简易实现

散列表（也称作HashMap、HashTable)

散列表的简易实现

处理散列表的冲突

应用

树数据结构

二叉搜索树简易实现

树的遍历

自平衡树 （AVL 与红黑树）

二叉堆（一种特殊的二叉树）

二叉最小堆的简易实现

应用

图

创建Graph类

图的遍历

应用

自平衡树（AVL 与红黑树）