十进制转二进制技巧

二进制共32位，初始都为0: 00000000 00000000 00000000 00000000 从右到左对应的是1 2 4 8 16 32 64 128 ……. 首位为符号位，正数为0，负数位1；

正数： 5转换为2进制： 5=4+1 所以为00000000 00000000 00000000 00000101（简写为101） 100转换为2进制： 100=64+32+4 所以为00000000 00000000 00000000 01100100（简写为1100100）

负数麻烦点： 1.写原码：先当正数，写出正数二进制，并将首位写成1， 2.写反码：每一位取反（除符号位） 3.写补码：正数的补码与原码相同，负数的补码为对该数的原码除符号位外各位取反，然后在最后一位加1. 最后补码也就是负数在计算机中的表示结果了。

-12： 12=8+4 原码：10000000 00000000 00000000 00001100 反码：11111111 11111111 11111111 11110011 补码：（11111111 11111111 11111111 11110011）+1 => 11111111 11111111 11111111 11110100 所以-12二进制表示为11111111 11111111 11111111 11110100

前言

平时的数值运算，其实是要先转换成二进制再进行运算的，而位运算就是直接进行二进制运算。
位运算是低级的运算操作，所以速度往往也是最快的（相对其它运算如加减乘除来说），并且借助位运算的特性还能实现一些算法。恰当地使用运算有很多好处。
前人用二进制、位运算给我们了一个操作简单的计算机，但我们却很少接触位运算了。
所有的位运算都是在二进制下来进行运算的，再二进制下只有0和1。

位运算符表

位运算分为两种，位逻辑运算符与位移运算符。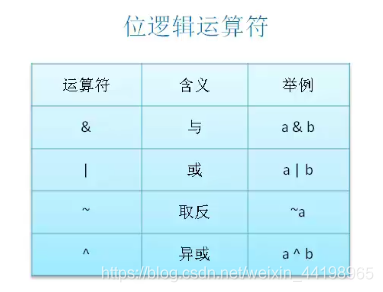
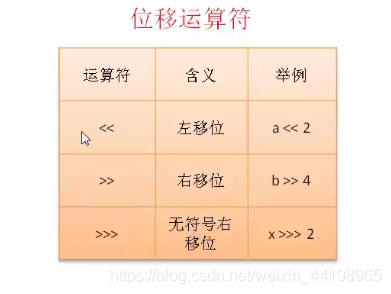
位运算符 - 图1位运算符 - 图2
位逻辑运算 - 逻辑结果参照表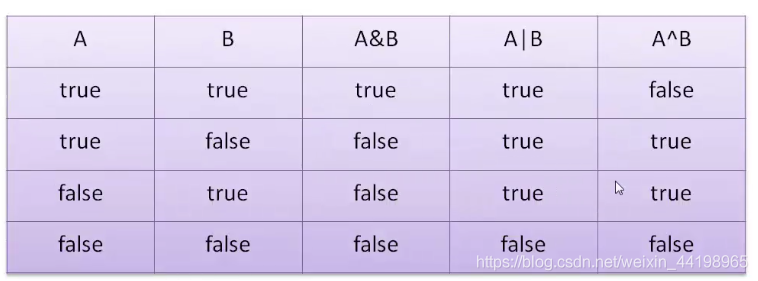
位运算符 - 图3
位逻辑运算 - 结果参照表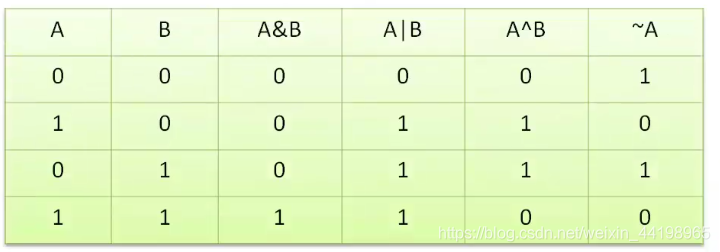
位运算符 - 图4

位运算符基础

&
按位与
如果两个相应的二进制位都为1，则该位的结果值为1，否则为0
|
按位或
两个相应的二进制位中只要有一个为1，该位的结果值为1
^
按位异或
若参加运算的两个二进制位值相同则为0，否则为1
~
取反
~是一元运算符，用来对一个二进制数按位取反，即将0变1，将1
<<
左移
用来将一个数的各二进制位全部左移N位，右补0
>>
右移
将一个数的各二进制位右移N位，移到右端的低位被舍弃，对于无符号数， 高位补0

使用位运算

（1）~ 位求反
运算符规则是：将运算符后二进制数反转，0变1，1变 0，所以对一个数取反偶数次结果是它本身。

  1. 0000 0000 0000 0000 0000 0000 0000 0011     -> 3
  2. 1111 1111 1111 1111 1111 1111 1111 1100     -> ~ 3 = -4

常用场景：
求相反数： ~a + 1
（2）<< 左移
运算符规则是：各二进位全部左移若干位，高位丢弃，低位补0。
例如：6 << 2 = 24

  1. 0000 0000 0000 0000 0000 0000 0000 0110     -> 6
  2. 0000 0000 0000 0000 0000 0000 0001 1000     -> 6 << 2 = 24

我们将6的二进位向左移动两位，低位补上两个0，高位丢弃，得出来的结果就是24。
常用场景：
左移常被用来做 (2 ^ n)的运算，因为直接基于二进制运算，所以左移效率比 (2 ^ n)高。
（3）>> 右移
运算符规则是：各二进位全部右移若干位，正数高位补0，负数高位补1，低位丢弃。
例如: 12 >> 2 = 3

  1. 0000 0000 0000 0000 0000 0000 0000 1100     -> 12
  2. 0000 0000 0000 0000 0000 0000 0000 0011     -> 12 >> 2 = 3

因为12是正数，右移过程中高位补上两个0，低位丢弃，得出来的结果就是3。
例如：-12 >> 2 = -3

  1. 1111 1111 1111 1111 1111 1111 1111 0100    -> -12
  2. 1111 1111 1111 1111 1111 1111 1111 1101    -> -12 >> 2 = -3

因为-12是负数，右移过程中高位补上两个1，低位丢弃，得出来的结果就是-3。
常用场景：
右移常被用来做 / (2 ^ n)的运算，因为直接基于二进制运算，所以右移效率比 / (2 ^ n)高。
（4）>>>无符号右移
运算符规则是：各二进位全部右移若干位，高位补0，低位丢弃。
例如: 12 >>> 2 = 3

  1. 0000 0000 0000 0000 0000 0000 0000 1100     -> 12
  2. 0000 0000 0000 0000 0000 0000 0000 0011     -> 12 >>> 2 = 3

我们将12的二进位向右移动两位，高位补上两个0，低位丢弃，得出来的结果就是3。
例如：-12 >>> 2 = 1073741821

  1. 1111 1111 1111 1111 1111 1111 1111 0100    -> -12
  2. 0011 1111 1111 1111 1111 1111 1111 1101    -> -12 >> 2 = 1073741821

我们将-12的二进位向右移动两位，高位补上两个0，低位丢弃，得出来的结果就是1073741821。
（5）& 位与
运算符规则是：运算符两边有0，结果就为0 ，只有当两边同时为1是，结果才为1。
如下：
0 & 0 = 0； 0 & 1 = 0； 1 & 0 = 0； 1 & 1= 1；
例如：3&5

  1. 0000 0000 0000 0000 0000 0000 0000 0011     -> 3
  2. 0000 0000 0000 0000 0000 0000 0000 0101     -> 5
  3. 0000 0000 0000 0000 0000 0000 0000 0001     -> 3 & 5 = 1

位与运算的特殊用途：
一、清零（将一个单元与0进行位与运算结果为零）
二、取一个数指定位（例如取num=1010 1101的低四位 则将num&0xF得到0000 1101）。
三、判断奇偶性：用if ((a & 1) == 0) 代替 if (a % 2 == 0)来判断a是不是偶数。
（6）| 位或
运算规则就是 运算符两边有1，结果就为1 ，只有当两边同时为0是，结果才为0。
如下：
0 | 0 = 0； 0 | 1 = 1； 1 | 0 = 1； 1 | 1 = 1 ；
例如:3|5

  1. 0000 0000 0000 0000 0000 0000 0000 0011     -> 3
  2. 0000 0000 0000 0000 0000 0000 0000 0101     -> 5
  3. 0000 0000 0000 0000 0000 0000 0000 0111     -> 3 | 5 = 7

另，负数按补码形式参加按位或运算。
使用场景：
下面这个方法是摘自HashMap类，这个算法来修改用户使用构造器传进来的size的，这个算法是使用移位和或结合来实现的，性能上比循环判断要好。

  1. public static final int tableSizeFor(int cap) {
  2.     int n = cap - 1;
  3.     n |= n >>> 1;
  4.     n |= n >>> 2;
  5.     n |= n >>> 4;
  6.     n |= n >>> 8;
  7.     n |= n >>> 16;
  8.     return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1;
  9. }

（7）^ 位异或
运算规则是：当运算符两边相同位置都是相同，结果返回0，不相同时返回1。
例如：3 ^ 5 = 1

  1. 0000 0000 0000 0000 0000 0000 0000 0011     -> 3
  2. 0000 0000 0000 0000 0000 0000 0000 0101     -> 5
  3. 0000 0000 0000 0000 0000 0000 0000 0110     -> 3 ^ 5 = 6

通常我们交换两个数会使用一个临时变量来帮忙：

  1. int t = a;
  2. a = b;
  3. b = t;

但是使用位运算，则不需要借助第三个变量。

  1. a ^= b;
  2. b ^= a;
  3. a ^= b;

负数的二进制表示方法

假设有一个 int 类型的数，值为5，那么，我们知道它在计算机中表示为：

00000000 00000000 00000000 00000101

5转换成二制是101，不过int类型的数占用4字节（32位），所以前面填了一堆0。

现在想知道，-5在计算机中如何表示？

　

在计算机中，负数以原码的补码形式表达。

什么叫补码呢？这得从原码，反码说起。

　

原码：一个正数，按照绝对值大小转换成的二进制数；一个负数按照绝对值大小转换成的二进制数，然后最高位补1，称为原码。

比如 00000000 00000000 00000000 00000101 是 5的 原码。

  1.       10000000 00000000 00000000 00000101 是 -5的 原码。

　

反码：正数的反码与原码相同，负数的反码为对该数的原码除符号位外各位取反。

取反操作指：原为1，得0；原为0，得1。（1变0; 0变1）

比如：正数00000000 00000000 00000000 00000101 的反码还是 00000000 00000000 00000000 00000101

负数10000000 00000000 00000000 00000101每一位取反（除符号位），得11111111 11111111 11111111 11111010。

称：11111111 11111111 11111111 11111010 是 10000000 00000000 00000000 00000101 的反码。

反码是相互的，所以也可称：

10000000 00000000 00000000 00000101 和 11111111 11111111 11111111 11111010互为反码。

　

补码：正数的补码与原码相同，负数的补码为对该数的原码除符号位外各位取反，然后在最后一位加1.

比如：10000000 00000000 00000000 00000101 的反码是：11111111 11111111 11111111 11111010。

那么，补码为：

11111111 11111111 11111111 11111010 + 1 = 11111111 11111111 11111111 11111011

所以，-5 在计算机中表达为：11111111 11111111 11111111 11111011。转换为十六进制：0xFFFFFFFB。

再举一例，我们来看整数-1在计算机中如何表示。

假设这也是一个int类型，那么：

1、先取-1的原码：10000000 00000000 00000000 00000001

2、得反码： 11111111 11111111 11111111 11111110（除符号位按位取反）

3、得补码： 11111111 11111111 11111111 11111111

可见，－1在计算机里用二进制表达就是全1。16进制为：0xFFFFFF

主要知识点：

正数的反码和补码都与原码相同。 而负数的反码为对该数的原码除符号位外各位取反。 负数的补码为对该数的原码除符号位外各位取反，然后在最后一位加1

下面是书上原文：

原码表示法规定：用符号位和数值表示带符号数，正数的符号位用“0”表示，负数的符号位用“1”表示，数值部分用二进制形式表示。 反码表示法规定：正数的反码与原码相同，负数的反码为对该数的原码除符号位外各位取反。 补码表示法规定：正数的补码与原码相同，负数的补码为对该数的原码除符号位外各位取反，然后在最后一位加1. 正零和负零的补码相同，[+0]补=[-0]补=0000 0000B