定义

每个结点至多有两上孩子结点
n（n>=0）个结点的有限集合

  1. n= 0时， 二叉树为空树
  2. n>0时，由根结点和两个互不相交的被称为根的左子树和右子树组成。左子树和右子树也分别是一棵二叉树

基本形态

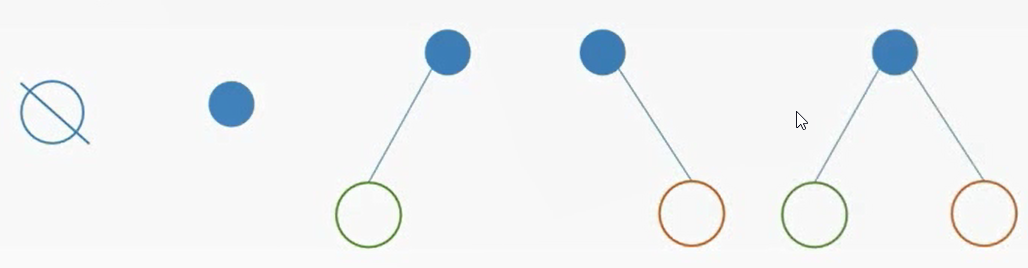
image.png

  • 二叉树的孩子结点有左右之分

二叉树与度为2的有序树区别？

  1. 二叉树可为空， 度为2的有序树至少有三个结点
  2. 二叉树的孩子结点始终有左右之分，而度为2的有序树孩子结点次序是相对的

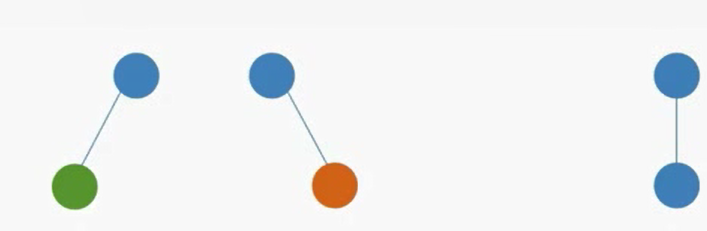
image.png

特殊二叉树

二叉树 - 图3

满二叉树

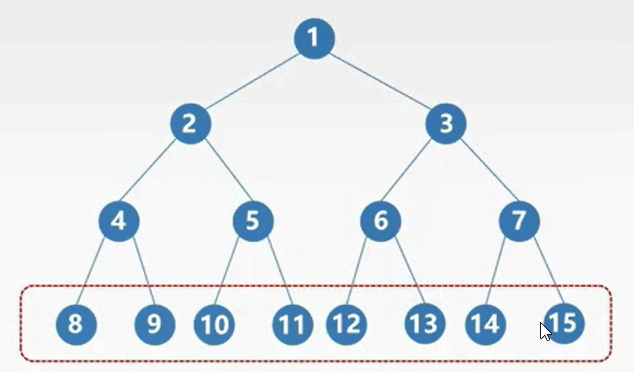
image.png

给结点从上向下， 从左向右编号，有以下特性：

  • 结点为i，
    • 左孩子=2i
    • 右孩子= 2i + 1
  • 编号为i的结点，其双亲的编号， i/2 取下限

完全二叉树

设一个高度为h、有n个结点的二叉树，当且仅当其每个结点都与高度为h的满二叉树中编号1~n的结点一—对应时，称为完全二叉树。

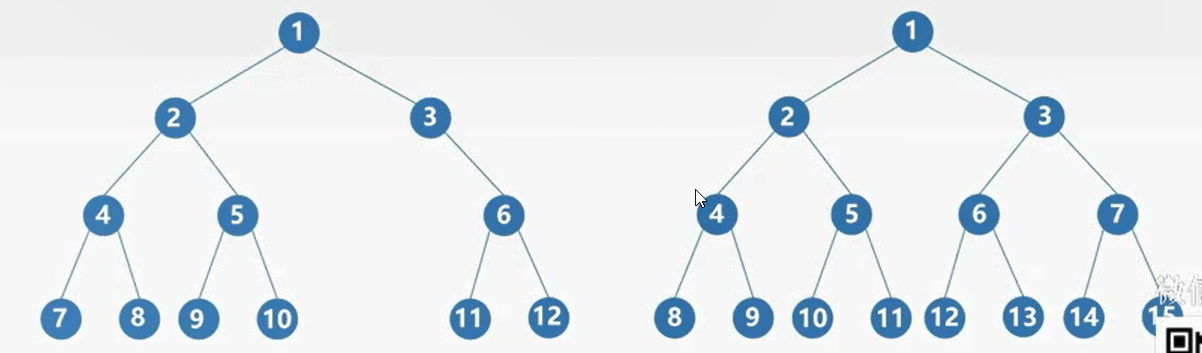
image.png

  • 编号6的结点不对应， 不称为完全二叉树

性质

  1. 若 i <= (n/2)取下限，则结点i为分支结点，否则为叶子结点
  2. 叶子结点只可能在层次最大的两层上出现。对于最大层次的叶子结点，都依次排在最左边的位置上。

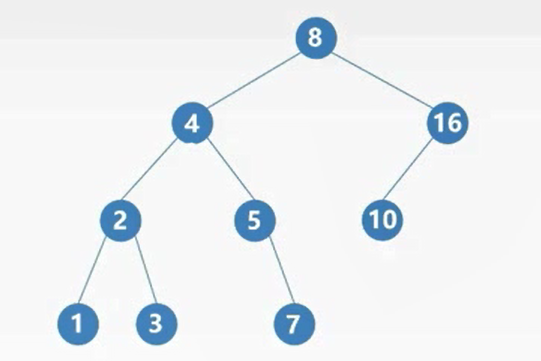
二叉排序树

一棵二叉树，若树非空则有如下性质：
对任意结点若存在左子树或者右子树，

  • 则其左子树上所有结点的关键字都 < 该结点，
  • 右子树上所有结点的关键字，都>该结点

image.png

平衡二叉树（红黑树）

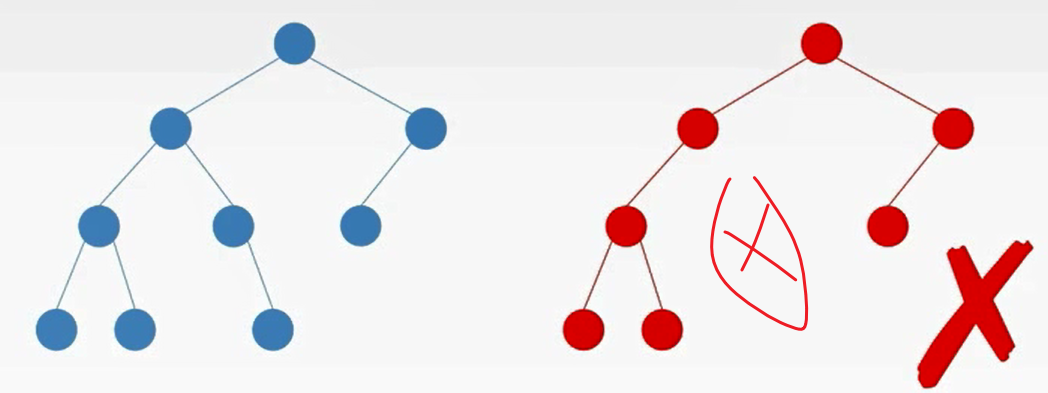
树上任意结点的左子树和右子树的深度只差不超过1

image.png

二叉树性质

二叉树存储

  • 顺序存储： （适合完全二叉树）
  • 链式存储

顺序存储

用一组连续的存储单元依次自上而下、自左至右存储完全二又树上的结点元素

顺序存储-完全二叉树
性质：
在完全二叉树中依次编号，对于结点i：
若存在左孩子，则编号为2i；若存在右孩子，则编号为2i+1

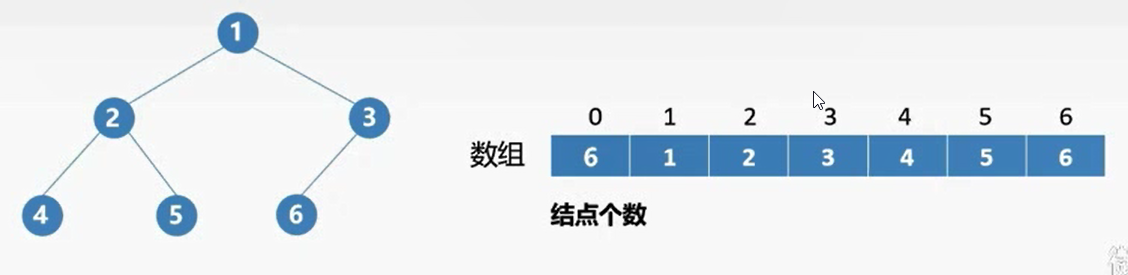
image.png

  • arr[0] 可以用来存储结点总数
  • 以上顺序存储基于“完全二叉树”

顺序存储-不完全二叉树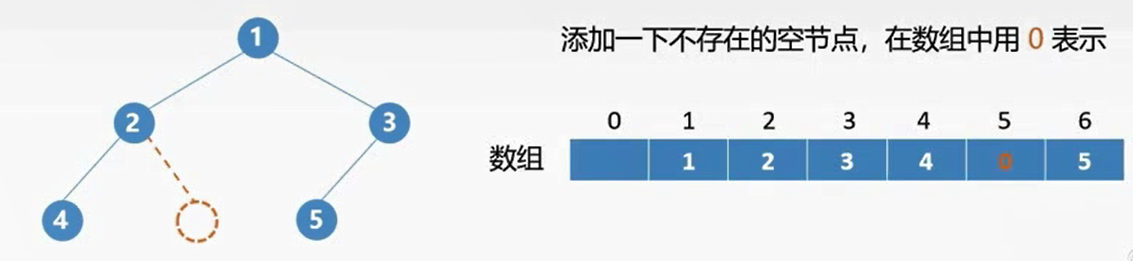
image.png

链式存储

用链表来存放一棵二叉树，二叉树中每个结点用链表的一个链结点来存储。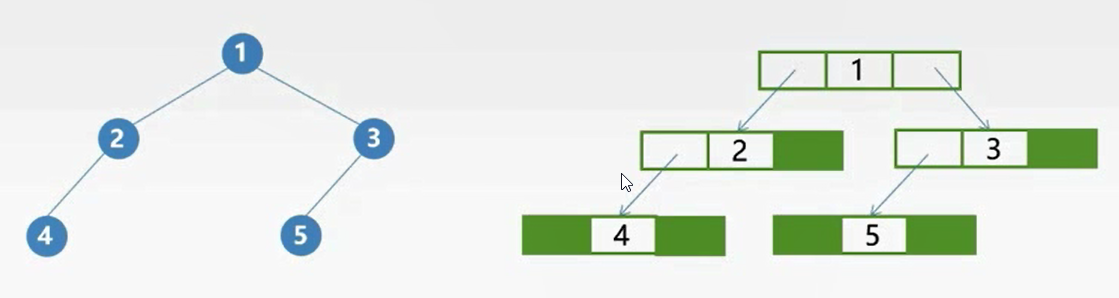
image.png

  • 含有n个结点的二叉链表中，有 n+1 个空链域 2n-(n-1)

场景

  1. 保存有序数据时，退化成