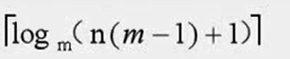基本概念

树：是 N（n>=0）个结点的有限集合，n= 0时， 称为空树
一种逻辑结构

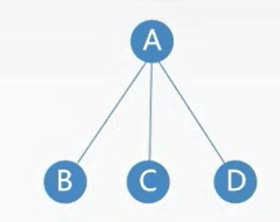
image.png

而任意非空对应该满足：

  1. 有且仅有一个特定的称为根的结点
  2. 当n>1时， 其余结点可分为m（m>0）个互不相交的有限集合，其中每一个集合本身又是一棵树，称为根结点的子树。

术语

描述各个结点之间的关系

树 - 图2 例子
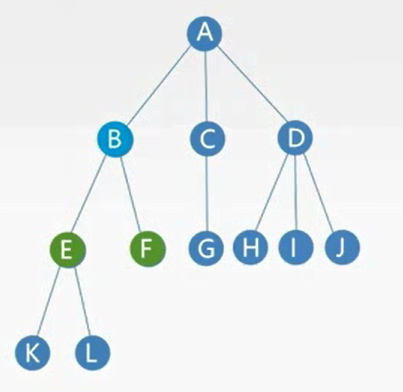
image.png

  • b的度为2，
  • d的度为3
  • 树的度为 3 （树中最大度数）
    • a的度为3
    • d的度为3

例子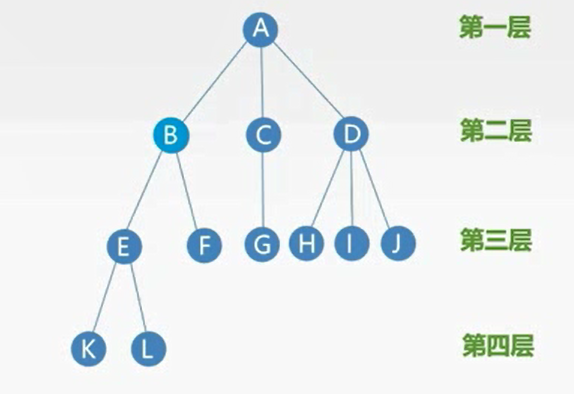
image.png

注意： 有些教材，根为第0层起算

  • B 的高度=3， 从下向中数
  • B 的深度 = 2，

  • 树的高（深）度， 是树中结点的最大层数


    分支
    树中的分支是有向的，即从双亲结点—>孩子结点，所以路径一定是自上而下的

例子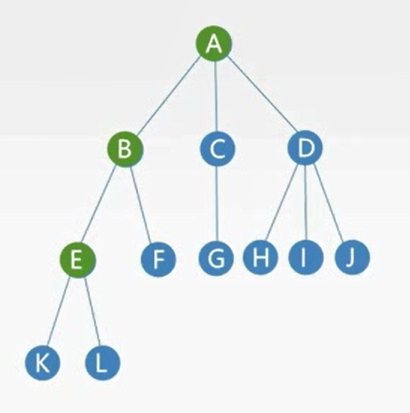
image.png

  • ae路径： {a, b, e}
  • ae路径长度： 2

森林

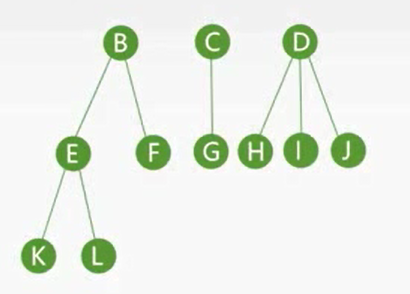
image.png

  • 三棵树
  • 一个森林

树的性质

树 - 图7

树中的结点数 == 所有结点的度数+1

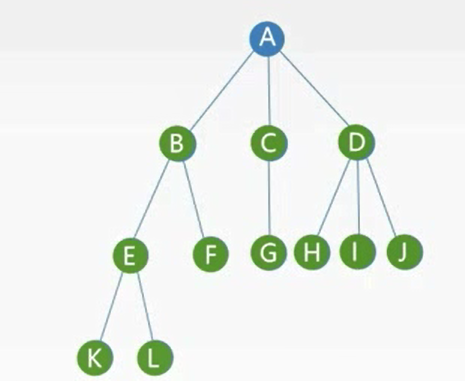
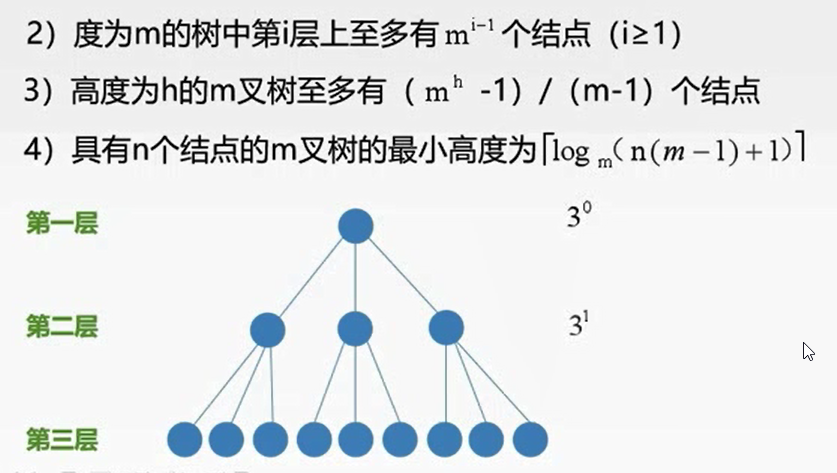
image.png

度为m的树，第i层上至多有m^(i-1)个结点（i>=1)

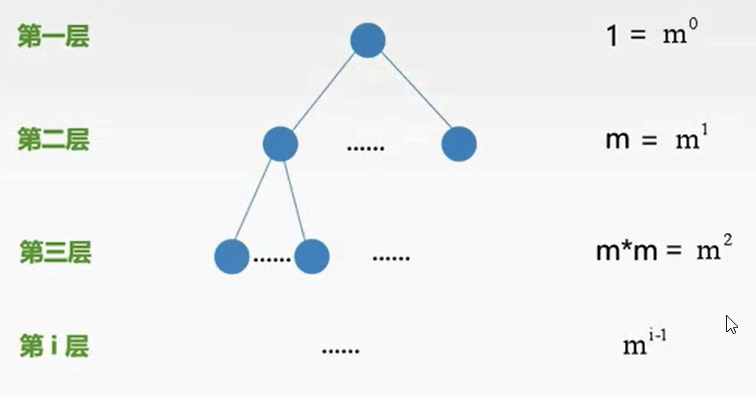
image.png

高度为h的m叉树，至多有(m^h -1)/（m-1）个结点

具有n个结点的m叉树的最小调试为
image.png

image.png