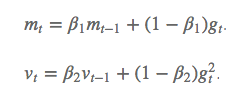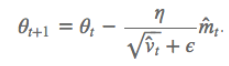数据类别不平衡时的处理方法

数据层面：

  1. 过采样
  2. 欠采样
  3. 数据增强
  4. SMOTE数据合成方法：在少量样本集中，对任何一个x，选择它的k近邻集合中的一个样本y，在x与y的连线上随机选取一点作为新合成的样本
  5. 代价敏感学习算法：在目标函数中，增加量少类样本被错分的损失值。

正则化

L1和L2的区别
L1范数（L1 norm）是指向量中各个元素绝对值之和，也有个美称叫“稀疏规则算子”（Lasso regularization）。
比如 向量A=[1，-1，3]， 那么A的L1范数为 |1|+|-1|+|3|.
简单总结一下就是：
L1范数: 为x向量各个元素绝对值之和。
L2范数: 为x向量各个元素平方和的1/2次方，L2范数又称Euclidean范数或Frobenius范数

  • L2正则化可以直观理解为它对于大数值的权重向量进行严厉惩罚，倾向于更加分散的权重向量。由于输入和权重之间的乘法操作，这样就有了一个优良的特性：使网络更倾向于使用所有输入特征，而不是严重依赖输入特征中某些小部分特征。 L2惩罚倾向于更小更分散的权重向量，这就会鼓励分类器最终将所有维度上的特征都用起来，而不是强烈依赖其中少数几个维度。。这样做可以提高模型的泛化能力，降低过拟合的风险。
  • L1正则化有一个有趣的性质，它会让权重向量在最优化的过程中变得稀疏（即非常接近0）。也就是说，使用L1正则化的神经元最后使用的是它们最重要的输入数据的稀疏子集，同时对于噪音输入则几乎是不变的了。相较L1正则化，L2正则化中的权重向量大多是分散的小数字。
  • 在实践中，如果不是特别关注某些明确的特征选择，一般说来L2正则化都会比L1正则化效果好。

[

](https://blog.csdn.net/liuweiyuxiang/article/details/99984288)

优化器

https://www.cnblogs.com/guoyaohua/p/8542554.html
梯度下降最常⻅见的三种变形：BGD、SGD、MBGD，这三种形式的区别是取决 于我们⽤多少数据来计算⽬标函数的梯度。

  • 梯度下降（GD）：使用所有训练数据的平均损失来近似目标函数。耗时大。
  • 随机梯度下降（SGD）：用单个训练样本的损失来近似平均损失。
    • 优点：适用于训练数据量大的情况。
    • 缺点：容易陷入局部最优。收敛不稳定。
  • AdaGrad：随着时间推移，学习率逐渐减小，保证算法最终收敛。
  • Adam：兼具动量（梯度更新的初始速度）和环境感知能力（记录梯度的一阶矩和二阶矩，分别是过往梯度与当前梯度的平均；过往梯度平方与当前梯度平方的平均）。
    • 优点：为不同参数产生自适应的学习率。

image.png
image.png