一. Stack 初识
Java 集合框架提供了一个集合Stack,它提供了stack 数据结构的功能,Java 中也提供了其他很多这样的集合,这种集合完成了某种数据结构的功能
1. stack 数据结构
栈是一种“后进先出”(LIFO)的线性数据结构,是一种特殊的线性表。
在栈中,元素的添加和删除操作只能在表的一端进行,即栈顶。元素的添加和删除遵循“后进先出”(LIFO)的原则,最后添加的元素总是最先出栈,栈对元素的访问加以限制,仅仅提供对栈顶元素的访问操作
在栈中,当栈有新元素加入时,将元素放入栈中,同时将栈顶指针top值加一,使其始终指向栈顶,当元素出栈时,栈顶top值减一,使其继续指向栈顶,直到top值为-1时,栈为空。
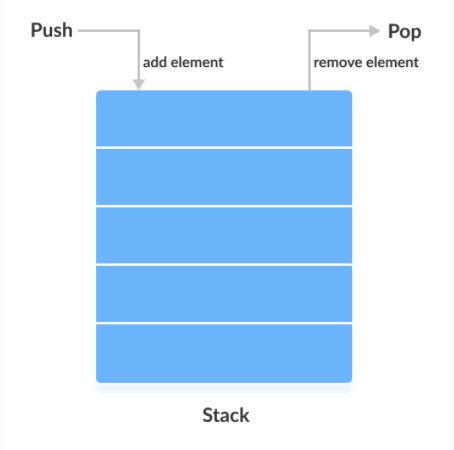
栈做为一种线性表,其实现方式主要有两种:数组和链表
2. stack 集合说明书
在看说明书之前,我们还是先看一下整个类的继承关系,让我们现有一个大致的轮廓
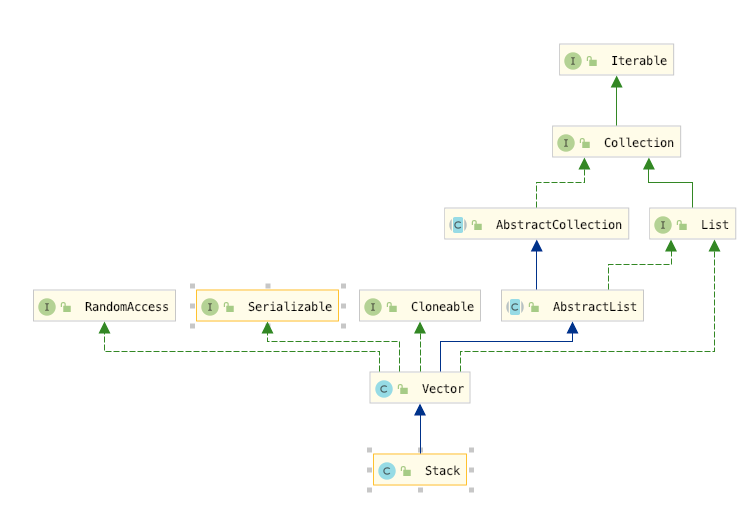
首先我们从这个上面的继承关系中,看到了stack 属于List 家族,和ArrayList 以及Vector 一样,但是需要注意的实它是继承自Vector 的,也就是说它是线程安全的
还有一点需要说明的是它是继承自Vector的,也就是说它底层是借助数组实现了Stack
/*** The <code>Stack</code> class represents a last-in-first-out (LIFO) stack of objects.* Stack 类代表了一种后进先出的的stack(数据结构)* It extends class <tt>Vector</tt> with five operations that allow a vector to be treated as a stack.* 它继承了Vector使用五种操作使得vector可以像stack一样* The usual <tt>push</tt> and <tt>pop</tt> operations are provided, as well as a method to <tt>peek</tt> at the top item on the stack,* a method to test for whether the stack is <tt>empty</tt>, and a method to <tt>search</tt>* the stack for an item and discover how far it is from the top.* 提供了常用的push和pop操作,以及一个查看栈顶元素的方法peek,一个测试栈是否为空的empty和一个查找元素并返回它距离栈顶元素的距离的方法search* When a stack is first created, it contains no items.* 当stack 被首次创建的时候,它不包含任何元素* <p>A more complete and consistent set of LIFO stack operations is provided by the {@link Deque} interface and its implementations,* {@linkdeque}接口和它的实现提供了一组更加完整和一致的后进先出堆栈操作集* which should be used in preference to this class. For example:<pre> {@code Deque<Integer> stack = new ArrayDeque<Integer>();}</pre>* 它应该被有限使用,这里给了一个例子Deque<Integer> stack = new ArrayDeque<Integer>();* @author Jonathan Payne* @since JDK1.0*/public class Stack<E> extends Vector<E> {}
3. stack 构造方法
二. Stack 的常用方法
因为 Stack 继承自 Vector 类,因此它集成了 Vector的所有方法. 关于Vector 的一切你可以看深度剖析Java集合之Vector 一篇,除了这些方法Stack 有自己特有的五个方法
1. push() 方法
我们使用push 方法向Stack添加提个元素
public class JavaStack {static Stack<String> animals = null;@BeforeAllpublic static void stack1() {animals = new Stack<> ();}@Testpublic void testPush(){animals.push("Dog");animals.push("Horse");animals.push("Cat");System.out.println("Stack: " + animals);}}// 输出结果Stack: [Dog, Horse, Cat]
接下来我们看一下源代码
public E push(E item) {addElement(item);return item;}
可以看到它实际上是调用了Vector 的addElement 方法,所以上面的代码中,可以看做是依次次将 Dog Horse 和 Cat 添加到了数组中,此时整个数组里的数据是这样存储的,因为我们知道addElement是依次元素到数组的末尾的,所以Cat 在最后面

需要注意的是push 方法是有返回值的
2.pop() 方法
删除栈顶元素并返回
@Test
public void testPop(){
animals.push("Dog");
animals.push("Horse");
animals.push("Cat");
System.out.println("Removed Before: " + animals);
String element = animals.pop();
System.out.println("Removed Element: " + element);
System.out.println("Removed After: " + animals);
}
输出结果
Removed Before: [Dog, Horse, Cat]
Removed Element: Cat
Removed After: [Dog, Horse]
因为我们从栈的定义知道,删除操作删除的实最后添加的元素,然后我们从push 方法知道了数组中数据的存放顺序,接下来,上面的输出证明了我们的想法,我们可以看到,删除了最后添加的Cat,也就是数组中最后面的一个元素,这就是栈的特点LIFO
那么这个时候我们猜测,pop 方法实际上调用的是Vector 的removeElementAt方法,传入的参数是最后一个元素的下标,也就是数组大小减去1,接下来我们从源码验证一下我们的猜想
public synchronized E pop() {
E obj;
int len = size();
obj = peek();
removeElementAt(len - 1);
return obj;
}
public synchronized E peek() {
int len = size();
if (len == 0)
throw new EmptyStackException();
return elementAt(len - 1);
}
其实我们看到和我们的猜想基本一致,不同的实这里为了返回要被删除的元素,先调用了elementAt方法,然后猜调用了removeElementAt 方法
这里有一个问题需要注意的是pop 是由synchronized 修饰的,其实pop 方法里面的调用的三个方法都是由synchronized 修饰的,这里你可以思考一下为什么该方法还要被synchronized修饰,其实这个就涉及到了一个问题,就是我们希望这三个方法被放在一起然后原子性执行,否则就不能保证逻辑的正确性
3.peek() 方法
返回栈顶元素
@Test
public void testPeek(){
animals.push("Dog");
animals.push("Horse");
animals.push("Cat");
System.out.println("Peek Before: " + animals);
String element = animals.peek();
System.out.println("Peek Element: " + element);
System.out.println("Peek After: " + animals);
}
输出结果
Peek Before: [Dog, Horse, Cat]
Peek Element: Cat
Peek After: [Dog, Horse, Cat]
这个代码就太简单了,然后就不解释了,但是需要注意一个问题,就是peek 方法会抛出异常,也就说你在调用的时候需要判断一下是否是空栈
public synchronized E peek() {
int len = size();
if (len == 0)
throw new EmptyStackException();
return elementAt(len - 1);
}
4.search()
search 方法可以返回特定元素以栈顶元素为基础在栈中的位置,其实就是返回这个方法在栈中的位置,然后栈中的第一个元素所在位置是1
@Test
public void testSearch(){
animals.push("Dog");
animals.push("Horse");
animals.push("Cat");
System.out.println("Search Before: " + animals);
int position1 = animals.search("Horse");
System.out.println("Search Horse Element: " + position1);
position1 = animals.search("Dog");
System.out.println("Search Dog Element: " + position1);
}
输出结果,因为Cat 的位置是1,所以我们可以看出其他的
Search Before: [Dog, Horse, Cat]
Search Horse Element: 2
Search Dog Element: 3
接下来我们看一下这个方法的实现
/**
* Returns the 1-based position where an object is on this stack.
* 返回以1 为基础的元素在stack 中的位置
* If the object <tt>o</tt> occurs as an item in this stack, this
* method returns the distance from the top of the stack of the
* occurrence nearest the top of the stack; the topmost item on the
* stack is considered to be at distance <tt>1</tt>. The <tt>equals</tt>
* method is used to compare <tt>o</tt> to the
* items in this stack.
* @param o the desired object.
* @return the 1-based position from the top of the stack where
* the object is located; the return value <code>-1</code>
* indicates that the object is not on the stack.
*/
public synchronized int search(Object o) {
int i = lastIndexOf(o);
if (i >= 0) {
return size() - i;
}
return -1;
}
本质上还是依赖数组的实现,首先找出了该元素在数组中倒数的位置距离,然后用数组大小减去了该距离
5. empty() 方法
检测栈是否为空
@Test
public void testEmpty(){
animals.push("Dog");
animals.push("Horse");
animals.push("Cat");
System.out.println(animals.empty());
System.out.println(new Stack<>().empty());
}
不为空返回false 为空返回true ,因为底层是Vector ,所以我们可以猜测这个方法的实现是依赖size 方法的,接下来我们看一下它的实现
public boolean empty() {
return size() == 0;
}
三. 总结
stack 集合实现了数据结构Stack 的定义,底层依赖Vector 实现也就是数组,对栈顶元素的操作实际上是对数组尾部元素的操作,因为这样可以避免数据的迁移

