第1章 数字设计方法概论
电路设计的经典设计方法是依赖于电路原理图的人工设计方法,而现在的大规模复杂电路广泛采用基于计算机语言的现代设计方法。原因是没有任何一支设计工程师团队能够用人工方法有效、全面、正确地设计和管理含有数百万门级的现代集成电路(IC)。
基于语言的设计易于移植且不依赖于工艺,设计团队也可以重用或修改以前的设计,以保持与更先进工艺的一致性。
硬件描述语言也是将各种设计专利成果集成为知识产权核(IP)的一种方便而有效的工具和手段。电路模块可以根据需要单独或合并进行综合和测试,以缩短设计周期。
HDL和综合工具的应用使得工程师们更关注有关功能的设计,而不是具体的单个晶体管或逻辑门的设计。
HDL可以作为多种设计工具的平台,包括:设计输入、设计验证、测试向量生成、故障分析和仿真、时序分析和验证、综合和原理图的自动生成等任务。
电路设计流程:基于HDL的ASIC设计流程
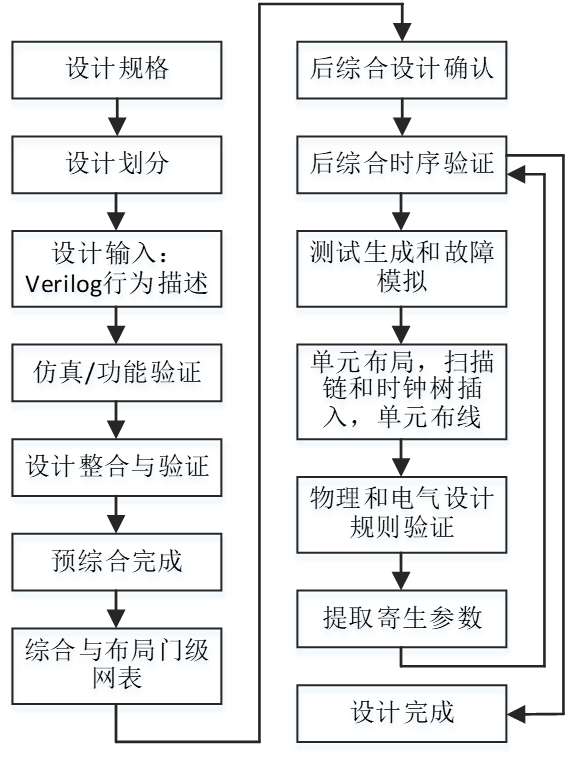
时序收敛:当所有的信号通路都满足由接口电路、电路时序单元和系统时钟所产生的时序约束条件时,即达到时序收敛。
1.1 设计方法简介
1.1.1 设计规格
设计规格书是一个非常详尽的设计技术描述文档,包括功能、时序、硅片面积,功耗、可测试性、故障覆盖率以及其他指导设计的相关准则等。
一般时序电路用包括状态转移图、时序图和算法状态机(ASM)图表描述。
1.1.2 设计划分
把大型电路划分为一个有多个相互关联的功能单元模块所组成的系统结构(architecture),其中每一个功能单元都能够具有描述其功能的行为模型。
把一个复杂系统的设计逐渐划分成规模较小且功能简单的单元电路,这样的划分过程通常被称为自顶向下(top-down design)或层次化(hierarchical design)的设计方法。
1.1.3 设计输入
设计输入是先形成一个基于语言描述的设计,并将其以电子格式的方式存储在计算机中。
基于HDL的设计通常在设计中通过使用描述名、加入明晰内容的注释、明确地指明结构的相互关系等文本内容的方式,从而减少了必须保存在其他归档文件中的文档 数量和内容。
行为建模描述一个设计的功能特性,即仅指定所设计的电路将要做什么,而无需指出怎样用硬件去构建电路。
1.1.4 仿真与功能能验证
设计的功能特性能够仿真或形式化方法来进行验证。
验证分为三个步骤:
- 拟定测试方案;
- 建立测试平台;
- 测试执行。
1.1.4.1 拟定测试方案
测试方案要认真组织、编写,以确定什么是要测试的功能特性和如何进行测试。测试方案应指定激励发生器、响应监测器以及判断被测模型的响应所需的有价值的参考判据。
1.1.4.2 建立测试平台
testbench是一个Verilog模块,在仿真时这个模块中的待测试单元(DUT)已被实例化,同时测试向量发生器也被施加到该模块的输入端。若一个设计为多模块结构形式,就要对它的每一个模块分别进行验证,从设计的最底层开始,然后再对整合设计进行测试来验证模块之间的相互作用是否正确。
1.1.4.3 测试执行和模型验证
testbench可根据测试方案进行完善,而且要对设计的原始指标对应的响应进行验证。找出设计中的错误所在、确定描述语法的正确性、检验习惯用法、为后续的综合工作消除障碍。
1.1.5 整合设计与验证
把功能子单元重新整合成一个完善的系统,再验证其功能特性正确与否。
需要对testbench重新进行开发,使其激励发生器能够实现上层模块的输入/输出功能,监测端口以及穿越模块边界时总线的活动,并且观察每个内嵌状态机的状态转换情况。
1.1.6 预综合完成
所有已发现的功能错误和问题均被解决后,即完成了预综合。
1.1.7 门级综合与工艺映射
通过综合工具创建一个最优布尔描述,并且利用一种有效工艺构建这个设计描述。
综合工具能够去除冗余逻辑,以寻求能实现功能特性并满足性能(速度)指标要求的最小面积的逻辑电路结构,这将产生一个标准单元网表或配置目标FPGA的数据库文件。
1.1.8 后综合设计确认
设计确认就是把已综合完的门级描述的响应与行为模型的响应相比较。
后综合设计确认能够发现行为模型在不同时钟周期触发产生非预期事件的软竞争情况。
1.1.9 后综合时序验证
从金属材料的特性以及制造掩模的几何形状等几个方面提取时延参数,并根据所提取的时延参数,利用静态时序分析器来验证最长的通路是否违反时序约束。
1.1.10 测试生成与故障模拟
用一组测试向量来测量电路的响应。
故障模拟研究的是从生产线出来的芯片是否能够通过测试来检验其工作情况正常与否。故障模拟的目的是为了确定一组测试向量是否能检测出一组故障。故障模拟的结果用于指导软件工具的使用以便生成更完备的测试模板或测试向量。
1.1.11 布局布线
布局与布线就是将设计单元适当地放置在晶片内,并连接信号通路。
1.1.12 物理和电器设计规则检查
对设计的物理布图进行检查是为了检查线宽、交叠、间隔等约束是否满足要求。电器规则检查是检查扇出约束是否满足,信号的完整性是否没有被电气串扰和电源栅压降所破坏。
1.1.13 提取寄生参数
版图所形成的寄生电容能够通过软件工具提取,并用所提取的参数对设计的电气特性和时序性能进行更精确的校验。
1.1.14 设计完成
在所有设计约束都已经满足,也达到了时序约束条件的情况下就会发出最终设计完成信号。掩模的格式是由几何数据(通常为GDS-II格式)构成的,这些数据决定了集成电路制造过程中的光刻步骤的顺序。
1.2 IC工艺选择
ASIC设计实现的物理方式有:
- 高性能电路的全定制版图;
- 标准单元结构;
- 门阵列(现场可编程或掩模可编程)。
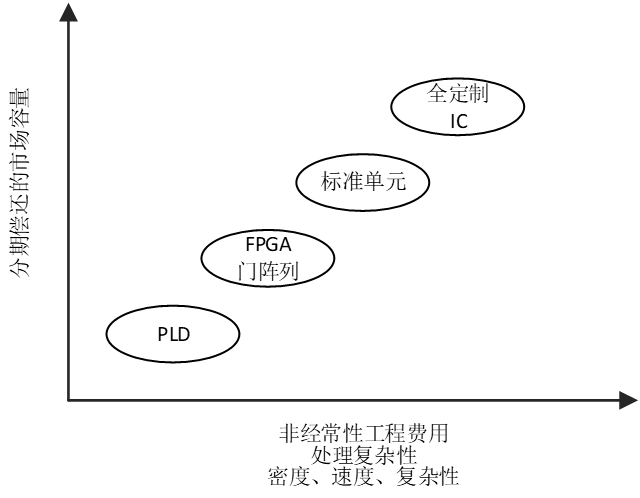
全定制IC具有高的性价比,但它需要有足够大的产量或者有足够多的用户群,还要有充足的开发时间和投资以便确保生产出面积最小和速度最高的全定制设计产品。FPGA具有固定及电可编程的结构,适合用于规模适中的设计实现。
掩模可编程门阵列工艺中,晶片上集成的晶体管阵列可以根据需求互连得到逻辑门电路,并实现所期望的功能。
标准单元工艺技术预先设计并特征化了掩模层的各个逻辑门,并封装在公用库中。利用布局布线工具把这些单元排放在晶片的相应通道位置,再进行互联,然后整合这些掩模,这样就可以制造出有特定应用功能的集成电路。
第2章 组合逻辑与布尔代数
2.1 组合逻辑与布尔代数
组合逻辑电路的输出可以表示为瞬时输入变量的布尔函数形式;当电路的输出与时刻t之前的历史输入有关时,则称这一类电路为时序逻辑电路,时序逻辑电路在硬件上需要采用存储单元来实现。
逻辑电路中的变量为二进制变量——其值为0或1,逻辑电路的硬件实现可以采用正逻辑,即用高电平(如5V)表示逻辑1,用低电平(如0V)表示逻辑0;也可以用负逻辑,用低电平表示逻辑1,用高电平表示逻辑0。
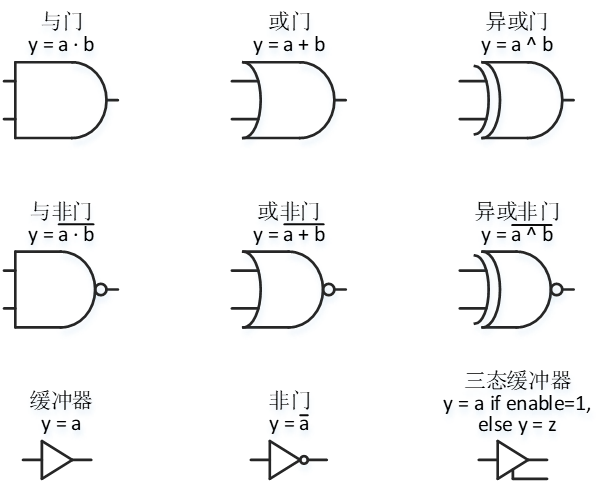
常用逻辑门电路的原理图符号与布尔关系式:
常用布尔逻辑符号与运算符号:
| 符号 | 逻辑操作 |
|---|---|
+ |
或 |
• |
与 |
⊕ |
同或 |
^ |
异或 |
' |
非 |
2.1.1 ASIC库单元
逻辑门实际上是由晶体管级电路实现的。
光掩膜技术有选择地在硅晶片上掺入杂质,从而形成晶体管及连接线。
实现基本的和较复杂的布尔函数表示的电路,可以用它们的功能、电气特性以及时序特性来描述,并且把这些电路封装后添加到标准单元库中。综合工具通过将逻辑综合的最终结果映射为单元库中的不同部件,来构造具有特定功能且满足性能要求的复杂集成电路。
2.1.2 布尔代数
逻辑电路的各种运算可以用布尔代数来描述,布尔代数由值集合以及运算符“
”和“
”组成。运算符“
”称为和运算符、或运算符或者逻辑加运算符;运算符“
”称为积运算符、与运算符或者逻辑乘运算符。
布尔代数法则:
| 布尔代数法则 | SOP格式 | POS格式 |
|---|---|---|
| 0组合率 | ||
| 1组合率 | ||
| 交换律 | ||
| 结合律 | ||
| 分配律 | ||
| 同一律 | ||
| 还原律 | —— | |
| 互补律 |
由个布尔变量扩展成的多维空间表示为
,
中的一个点称为一个顶点,并且可以表示成元素为二进制数字的一个
维向量。
一个完全确定的具有个输入的
维布尔函数是一个从
到
的映射,记为
,一个非完全描述的函数则在
的子集上,而且认为它在定义域外的点具有无关项:
,其中
表示无关项。
一个布尔函数的集合是由使函数成立(逻辑真)的顶点组成,即
;
集合则是由函数不成立(逻辑假)的顶点组成,即
;而无关项(
)集合是由对函数取值没有确定的顶点组成,因此有
,无关项集合包含不可能出现的输入组合或输出不可能发生的情况。
2.1.3 狄摩根定律
狄摩根定律(DeMorgan)可以将积之和形式的电路转换为和之积形式的电路,也可以反过来转换。
多项式之和的补为:
多项式之积的补为:
2.2 布尔代数化简定理
化简布尔表达式的定理:
| 定理 | SOP形式 | POS形式 |
|---|---|---|
| 逻辑相邻 | ||
| 吸收或 | ||
| 乘法与因式分解 | ||
| 一致性 |
香农(Shannon)表达式:
其中,。布尔函数
的布尔微分为
函数对
的布尔微分决定了
是否对输入变量
的变化敏感。利用该性质,通过布尔代数方法可以确定一次测试是否可以检测出该电路的一个故障,而且应用香农展开式也可以递归生成布尔函数的二进制树映射。
2.3 组合逻辑的表示
组合逻辑的三种常用的表示方法:
- 结构化(即门级)原理图;
- 真值表;
- 布尔方程。
二进制判定图(BDD)法,是一种布尔函数的图形表示法,它包含可实现布尔函数时所需的信息。
2.3.1 积之和表示法
逻辑变量的乘积构成一个与项,其中的逻辑变量可以是原变量形式也可以是反变量的形式。与项无需包含每个逻辑变量,一个布尔表达式由一组与项构成,其典型表达式为积之和形式,即与项的“或”运算。
积之和形式的布尔表达式中的各与项称为该函数的蕴涵项。最小项是指含有该函数所有变量的一个与项,所包含的变量可以是原变量形式(非补形式),也可以是反变量形式(但两种形式不能同时出现)。
如果每一个与项都包含了各变量以原变量或反变量形式出现的所有变量,则称该积之和形式的布尔表达式是标准或规范的SOP形式。一个规范的(标准的)积之和函数同样也被称为标准积之和(SSOP)。用十进制数表示最小项时,与十进制数相等的二进制数表示形式中的1和0分别代表逻辑变量的原变量或反变量。一个布尔函数就是一组使函数成立的最小项(顶点)集合,积之和形式的布尔函数可以表示为最小项之和的形式。
2.3.2 和之积表示法
布尔函数也可以用和之积的形式来表示,即布尔因子相乘的形式,其中每个布尔因子式都是逻辑变量之和。
在积之和形式的布尔表达式中,如果每一个因子包含了所有变量的以原变量或反变量形式(但任何一个变量的原变量、反变量的形式不能同时出现)出现的逻辑变量,则称该和之积形式的布尔表达式为规范的或标准的POS形式。
最大项是基于或运算的逻辑变量之和,其中每个变量以原变量或者反变量的形式仅仅出现一次。最大项序号的十进制表示是根据函数真值表中函数值为0的行得到的,且对这些行中的逻辑变量值取反以得到最大项序号。
2.4 布尔表达式的化简
如果积之和形式的布尔表达式包含最小的乘积项和最少的字符变量(即表达式中的任何一个给定项都不能被其他逻辑变量数更少的项所代替),则称该积之和形式的布尔表达式是最简的。
布尔表达式化简的4种常用方法:
- 手工作图法:借助卡诺图来表示函数的逻辑相邻性;
- 奎恩-麦克罗斯基(Quine-McCluskey)化简算法:算法借助逻辑相邻性,使用与卡诺图同样的原理进行化简;
- 布尔化简法:巧妙应用描述布尔变量间关系的定理来寻找更简单的、等价的表达式;
- 现代综合工具化简法:将布尔化简法中使用的定理嵌入到现代综合工具程序中,用这些综合工具和程序进行逻辑化简。
在布尔表达式中,包含在另一个与项中的与项称为冗余项。布尔表达式中不存在与项的相互包含关系,则称该表达式为非冗余的。
布尔化简之所以困难是因为一个布尔表达式最简的积之和形式与最简的和之积形式都不一定是唯一的。
使用逻辑相邻性,通过以下两种方法化简:
- 反复合并那些仅有一个逻辑变量不同的乘积项;
- 删除冗余蕴涵项。
质蕴涵项是一个没有完全包含在该函数其他与项的顶点集合中的与项。质蕴涵项不能与其他蕴涵项合并而消去一个逻辑变量,也不能利用吸收律将该项从表达式中消除。一个布尔表达式的质蕴涵项集合是唯一的。
没有被其他任何蕴涵项集合所覆盖的质蕴涵项称为主质蕴涵项,主质蕴涵项必须包含在函数的覆盖中。
化简布尔表达式的步骤:
- 找出由所有质蕴涵项组成的集合;
- 找出覆盖所有质蕴涵项的最小蕴涵项子集(包括主质蕴涵项),一个布尔表达式的最小覆盖就是覆盖其所有质蕴涵项的一个质蕴涵项的子集。
某些情况下,在一个表达式中引入冗余项对使用吸收律和逻辑相邻性是有帮助的,对于一个积之和形式的布尔表达式,采取如下步骤:
- 增加一个逻辑变量及其反变量的乘积;
- 增加冗余项;
- 为一个逻辑变量加上该逻辑变量与其他任意逻辑变量的乘积项。
对一个和之积形式的布尔表达式采取下列步骤:
- 一个表达式乘以一个由任意逻辑变量及其反变量之和组成的因式;
- 引入乘积冗余性因式;
- 用一个逻辑变量乘以该变量与其他任意逻辑变量之和的因式。
2.4.1 卡诺图(积之和形式)
卡诺图提供了一种适用于最多含有5个变量或6个变量的布尔函数的图形化或形象化表达形式。逻辑函数布尔域中的各个顶点可用图中的一个方格表示,图中各个方格单元都有一个标识来分别表明其相应的顶点属于真集
、假集
或无关项集
。
一个卡诺图的最上边与最下边一行是逻辑相邻的,最左边一列与最右边一列也是逻辑相邻的。含有的逻辑相邻单元可以合并,逻辑上相邻的方格可以合并。

