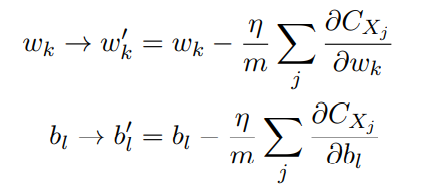注：（思考-神经元设置与非线性函数的作用）
1.1 感知机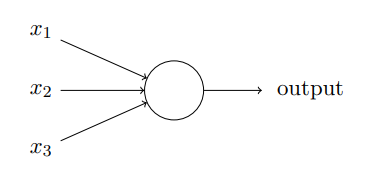
- 接受几个二进制输入（可以更少）
- 对于不同的输入 Xi 有对应的权重值 Wi
- 对于不同输入的权重设定 取决于 该输入 对 输出结果 的重要性
- 输出（0 或 1）
- 取决于 所有输入与权重的成绩之和WiXi 与 所设定阈值threshold 的比较结果决定
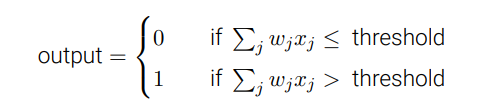
1.2 数学表达
- 让我们简化感知器的数学描述。条件
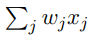看上去有些冗⻓，我们可以创建两个符号的变 动来简化。第⼀个变动是把 
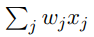改写成点乘 w · x，这⾥ w 和 x 对应权重和输⼊的向量。 - 第⼆个变动是把阈值移到不等式的另⼀边，并⽤感知器的偏置 b ≡ −threshold 代替。 ⽤偏置⽽不是阈值，那么感知器的规则可以重写为：
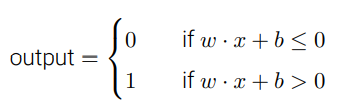
如此基础下的感知机只能被认为是一种新型的与非门，因此我们应该考虑设计一种学习算法，能够⾃动调整⼈⼯神经元的权重和偏置。这种调整可以响应外部的刺激，⽽不需要⼀个程序员的直接⼲预。
这些学习算法是我们能够以⼀种根本区别于传统逻辑⻔的⽅式使⽤⼈⼯神经元，我们的神经⽹络能简单地学会解决问题，这些问题有时候直接⽤传统的电路设计是很难解决的。
2.1 S型神经元
我们需要设计一种学习算法来使权重（或偏置）的微小改动能引起输出的微小变化 ，但是实际上感知机的输出只能为（0或1），因此很难通过改变权重（或偏置）来纠正输出结果，很有可能改变后对于该系统⽹络中单个感知器的输出结果有所翻转，但可能引起其余⽹络的⾏为以极其复杂的⽅式完全改变。
因此引入S型神经元，与感知机大部分相同，改变的仅仅是输出函数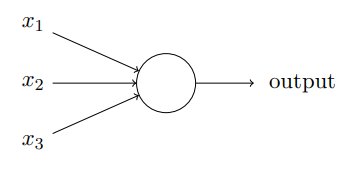
输出为 σ(w · x+b) ，而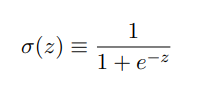
因此输出将不再仅仅局限于 0或1，而是推及到0-1之间的任意取值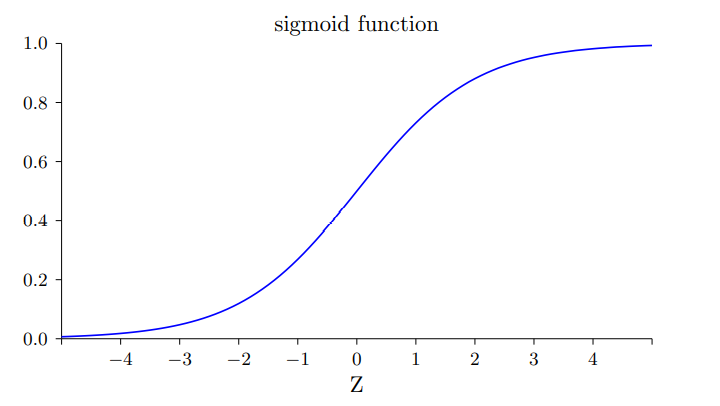
当取值从非0即1更变为0-1之间的任意取值后，我们的学习算法便可以更轻松的实现了，输出可以用以下式子表示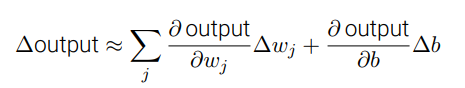
由此式可见，每一个权重或偏置的微小变化都将使输出有一定的变化，目前看来，这也就实现了我们所希望的学习算法，并且可以通过层层求导来获取他们之间的关系。
（易证明在一定条件下，输入保持不变，同样结构的S型神经元的输出结果非常近似于同结构的感知机的输出，在此就不赘述。）
3.1 代价函数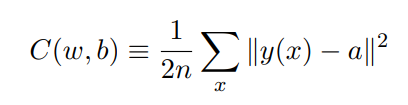
这⾥ w 表⽰所有的⽹络中权重的集合，b 是所有的偏置，n 是训练输⼊数据的个数，a 是表 ⽰当输⼊为 x 时输出的向量，求和则是在总的训练输⼊ x 上进⾏的。输出 a 取决于 x, w 和 b
代价函数所表示的意义是：对于 所有输入 x 所对应的神经网络输出 a 与其真实值 y(x)之差 的模 的平方 的平均值
- 即当预测结果较为准确时 C(w,b)≈0，而预测结果相差较大时，C(w,b)的值也相对较大
- 因此我们的学习算法最终目标就是不断更新 w和b 来使C(w,b)的值尽可能小甚至等于0
- 注： 为什么要介绍⼆次代价呢？毕竟我们最初感兴趣的内容不是能正确分类的图像数量吗？为什 么不试着直接最⼤化这个数量，⽽是去最⼩化⼀个类似⼆次代价的间接评量呢？
- 这么做是因为 在神经⽹络中，被正确分类的图像数量所关于权重和偏置的函数并不是⼀个平滑的函数。
- ⼤多数情况下，对权重和偏置做出的微⼩变动完全不会影响被正确分类的图像的数量。这会导致我们很难去解决如何改变权重和偏置来取得改进的性能。
- ⽽⽤⼀个类似⼆次代价的平滑代价函数 则能更好地去解决如何⽤权重和偏置中的微⼩的改变来取得更好的效果。
4.1 使⽤梯度下降算法进⾏学习
我们想象有⼀个 ⼩球从⼭⾕的斜坡滚落下来。我们的⽇常经验告诉我们这个球最终会滚到⾕底。也许我们可以 ⽤这⼀想法来找到函数的最⼩值？我们会为⼀个（假想的）球体随机选择⼀个起始位置，然后 模拟球体滚落到⾕底的运动。
找到一个（最大）梯度 ∇C ，则每次更新为： v → v ′ = v − η∇C （ η为学习率，一个极小的正数）
缺点（问题）：
- 无法取得全局最小值
4.2 随机梯度下降
思路：通过随机选取⼩量训练输⼊样本来计算 ∇Cx，进⽽估算梯度 ∇C。通过计算少量样本的平均值我们可以快速得到⼀个对于实际梯度 ∇C 的很好的估算，这有助于加速梯度下降，进⽽加速学习过程。
- 为了将其明确地和神经⽹络的学习联系起来，假设 wk 和 bl 表⽰我们神经⽹络中权重和偏置。 随机梯度下降通过随机地选取并训练输⼊的⼩批量数据来⼯作
- 其中两个求和 是在 当前⼩批量数据中 的 所有训练样本 Xj 上进⾏的。然后我们再挑选另⼀随机选定的⼩批量数据去训练。直到我们⽤完了所有的训练输⼊（即整个数据集），这被称为完成了⼀个训练迭代期（epoch）。然后我们就会开始⼀个新的训练迭代期。
若有收获，就点个赞吧
0 人点赞
