数据结构KMP算法配图详解

解决问题类型

KMP算法的作用是在一个已知字符串中查找子串的位置,也叫做串的模式匹配。 :::info 给你两个字符串 haystack 和 needle ，请你在 haystack 字符串中找出 needle 字符串出现的第一个位置（下标从 0 开始）。如果不存在，则返回 -1 。
输入：haystack = “hello”, needle = “ll” 输出：2 :::

操作流程

• 假设现在文本串 S 匹配到 i 位置，模式串 P 匹配到 j 位置
• 如果 j = -1，或者当前字符匹配成功（即 S[i] == P[j] ），都令 i++，j++，继续匹配下一个字符；
• 如果 j != -1，且当前字符匹配失败（即 S[i] != P[j] ），则令 i 不变，j = next[j]。此举意味着失配时，模式串 P相对于文本串 S 向右移动了 j - next [j] 位
• 换言之，将模式串 P 失配位置的 next 数组的值对应的模式串 P 的索引位置移动到失配处

算法内容概念

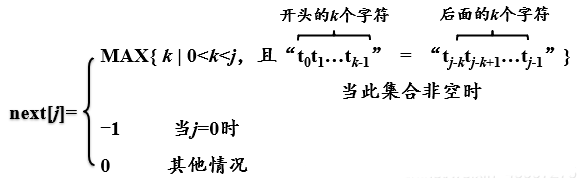
next数组

用一个next数组存储子串的最长相等前后缀的长度。而且next数组的数值只与子串本身有关。
所以next[i]=j,含义是：下标为i 的字符前的字符串最长相等前后缀的长度为j。 :::warning 子串t= “abcabcmn”的next数组为next[0]=-1(前面没有字符串单独处理)
next[1]=0；next[2]=0；next[3]=0；next[4]=1；next[5]=2；next[6]=3；next[7]=0； :::

“提示”示例代码

public class Solution
        {
            public int StrStr(string haystack, string needle)
            {
                // 排除子串为空
                if (string.IsNullOrEmpty(needle))
                {
                    return 0;
                }
                // 排除子串字长大于匹配字符串以及匹配字符串为空
                if (needle.Length > haystack.Length || string.IsNullOrEmpty(haystack))
                {
                    return -1;
                }
                // 调用KMP算法
                return KMP( haystack, needle);
            }
        }
        private static int KMP(string haystack, string needle)
        {
            // 创建 next数组：最长匹配长度+1
            int[] next = GetNext(needle);
            // 字符串下标
            int i = 0;
            int j = 0;
            // KMP判断循环
            while (i < haystack.Length)
            {
                if (haystack[i] == needle[j]) // 字符相等，两者各进一步
                {
                    j++;
                    i++;
                }
                if (j == needle.Length)
                {
                    return i - j;
                }
                else if (i < haystack.Length && haystack[i] != needle[j])
                {
                    if (j != 0)
                        j = next[j - 1];
                    else
                        i++;
                }
            }
            return -1;
        }
        // 计算获取next数组内的值
        private static int[] GetNext(string str)
        {
            int[] next = new int[str.Length];//数组内元素个数等于子串字符数
            next[0] = 0;
            int i = 1;// 指针初始位
            int j = 0;// 元素值
            while (i < str.Length)
            {
                if (str[i] == str[j])
                {
                    j++;
                    next[i] = j;
                    i++;
                }
                else
                {
                    if (j == 0)
                    {
                        next[i] = 0;
                        i++;
                    }
                    // 回溯
                    else
                    {
                        j = next[j - 1];
                    }
                }
            }
            return next;
        }