聚类解决的是分类具有相同特征的数据，将他们聚成一簇。
聚类问题不能通过暴力法进行穷举，因为数据不同，分类不同可能出现的情况过多，因此是一个NP问题，

物种形成

达尔文的进化观点中，生物种群竞争而达到选择的最优解，因此对于物种形成和研究和对进化论建模时，就需要用到K均值分析。
K均值算法有多种表达形式，例如Floyd算法或是其它的修正算法

训练集的学习方法

非监督类学习

非监督类学习指的是算法不知道那个数据属于哪个种类，例如鸢尾花，只给出数据而不给定类别，算法通过数据之间的相似度来区分数据。将相似的数据聚合到一起归为一类。
对于鸢尾花来说，K均值算法是不要求数据集进行归一化的。
因为归一化是数据的一个或者多个特征量过大，则必须进行归一化，鸢尾花的数据集四个比率量特征值都比较接近。
使用非监督类学习必不能让算法区分出鸢尾花的种类，因为数据自身的原因。有的数据对于K均值来说可能很简单很准确，但是鸢尾花的数据集属于不能直接看出来的一类，而且不能通过一条线来分割各类，因此不是线性可分的，使用非监督类学习并不能解决问题。

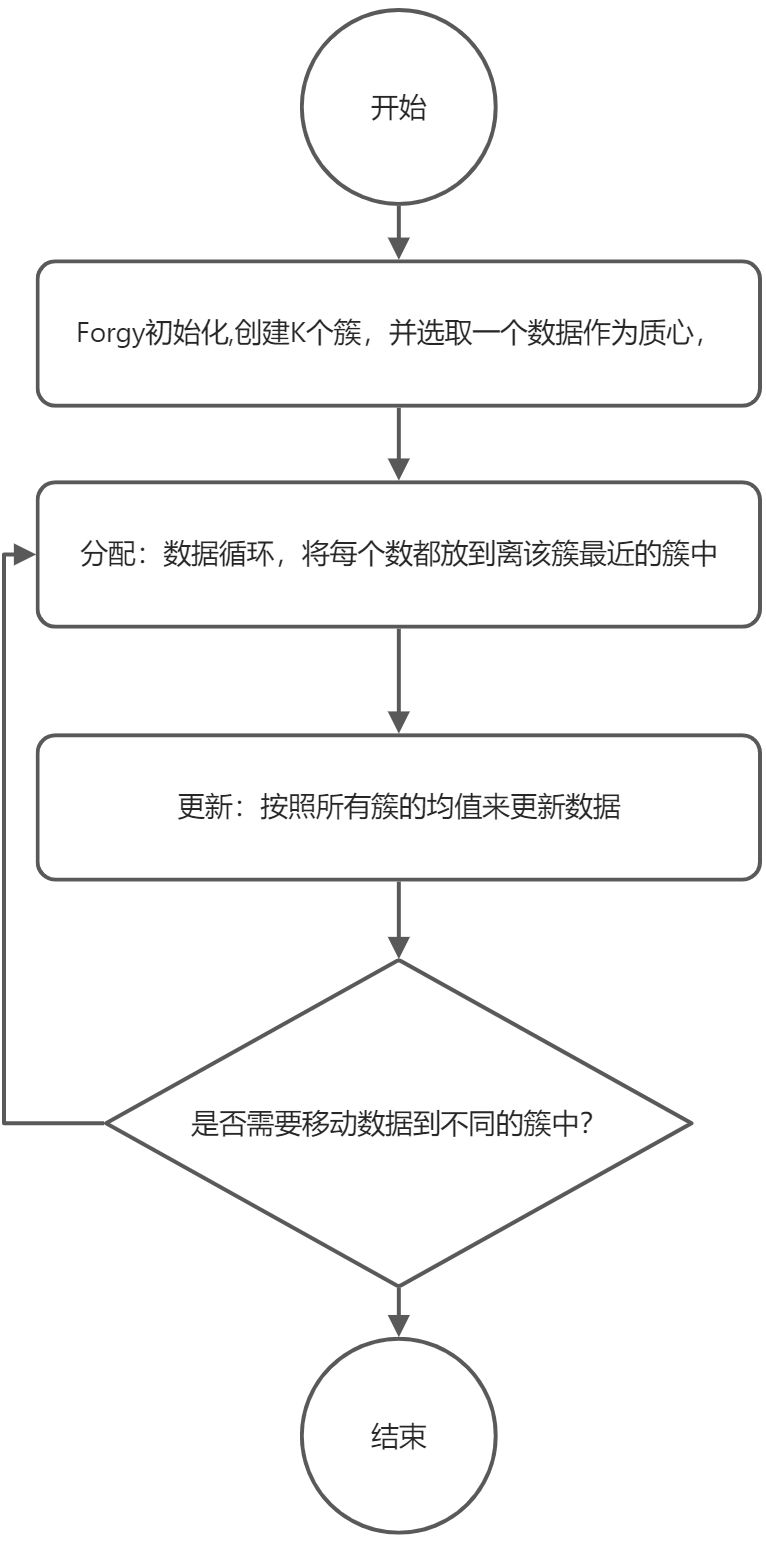
K均值聚类概念

聚类算法有三个步骤：

1. 初始化
2. 分配
3. 更新

对于上面的三个步骤而言，初始化这个步骤是非确定性的，也就是算法不是确定的，而分配和更新的算法都是确定性的，因此初始化方法较为复杂一些。

初始化方法

随机初始化：

对于一个数据而言，随机初始化的成本较低，而且对后续的迭代过程影响不大。

1. 创建K个簇
2. 将每个数据都随机分配到某个簇中
3. 去掉所有空的簇

   Forgy初始化