归一化概念

在统计学中数据被分为两类：第一类是性质量，描述某现实物体的性质，第二类是数字量，包括数量和数字。
例如一杯咖啡：
咖啡的性质量可以有：

• 颜色深浅
• 散发的气味
• 烫不烫手

咖啡的数字量可以有：

• 一共300毫升
• 热量450焦耳
• 温度30摄氏度
• 单价12元

这些带有量纲的数字也可描述咖啡。
对于这两种类型的数据，还可以被细分如下：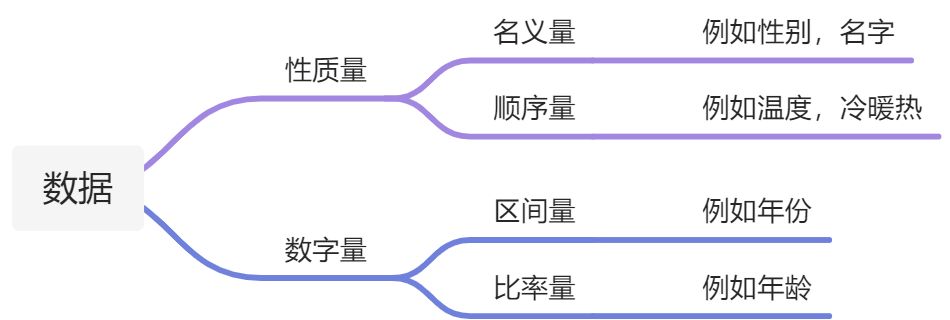

很显然名义量和顺序量是定性观测的，而区间量和比率量是定量观测的。

归一化的必要性

上文中的四个量是要交给人工智能去处理的，而性质量的名义量和顺序量本身并不是数据，可能是文字或是描述，有必要将其转化为算法所需要的浮点数。
有些算法需要将所有数据转为区间量，通常是（1，0）。之所以要归一化，是因为我们常见的数据存在量纲，也就是单位，他们常常无关且相差巨大，这对计算机要求的通用性而言是不合理的，例如在生活中我们通常使用百分数来描述趋势，比如某物品涨价了20%，这种无关数据本身却能描述数据变化，一万元的商品涨价20%和十块钱涨价20%都是相同的意义。

名义量的归一化

名义量有两个常用方法：凸显算法和等边编码法。
突显算法是通过某个名义在同类名义中得出的。例如鸢尾花的种属，一共有三种：Setosa，Versicolor和Virginica，其中Setosa定义为1，那么其余的都为0，就得到了如下的编码方案：
Setosa [1,0,0]
Versicolor[0,1,0]
Virginica[0,0,1]

顺序量的归一化

用学业举例子，9年义务教育从小学一年级一直到初中三年级。一共九个，那么就有了如下的编码方案；
小学一年级：0
小学二年级：0.125
小学三年级：0.25
小学四年级：0.375
小学五年级：0.5
小学六年级：0.625
初中一年级：0.75
初中二年级：0.875
初中三年级：1
其中小学一年级是最小的，初中三年级是最大的。
上面的例子是(0,1)区间的,如果区间是(1,-1)或是其他区间,就需要重新映射.

顺序量归一化步骤:

1. 将数据化为百分数: rate = number / total
2. 求区间宽度:width = (high-low) 区间上限减去区间下限
3. 百分数与区间宽度相乘: widthDistance = width * rate
4. 再将求得的值加到区间下限上 LowerBound + widthDistance

可以总结为：

解归一化

也就是将归一化的数据解释为我们需要得到是实际数据,例如得出的0.75想要变为原来的初中一年级,就可以通过下式:

数字量归一化

第一步确定数据的上下限,也就是归一前的数据上下限
第二部确定数据归一后的区间上下限,一般为0~1
第三步求得数据的宽度:

第四步计算输入数据离下限的距离：
例如上一节的900 / 3900 = 0.23
再将该数据带入到归一化后的宽度中
可总结为
同理，解归一化可总结为：

倒数归一化

倒数归一化是一种非常简单的归一化，因为区间只能是（-1，1）因此只需要将数据带入下式即可：
,巧合的是归一化和解归一化使用的是一个式子.

等边编码

有些突显编码无法解决的问题可以被等边编码有力的解决.
等边编码有如下优势:

1. 需要输出的通道比突显编码少
2. 更有效的说明数据间差异

等边编码是基于欧氏距离得出的,输出的结果可以被理解为距离正确结果最近的距离.
欧氏距离可由下式求得:

q代表理想输出值
p代表实际输出值

等边编码程序化

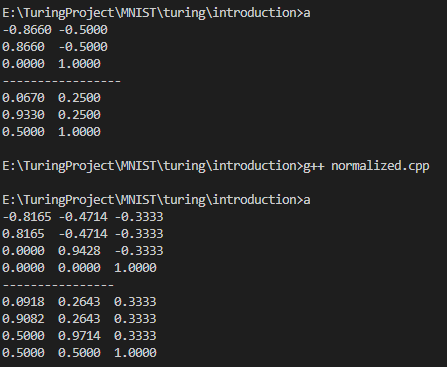
等边编码的目标是输出一个N*(N-1)的矩阵,N为类别数量,矩阵的每一行都代表某个类别的编码结果.且所有元素的值都被归一化到(-1,1)区间内.最终放缩到目标区间.

#include <iostream>
#include <math.h>
const int N = 4;    // given N for result
double result[N][N];
int main(){
    double f = 0.0; // 放缩因子
    double r = 0.0; // 倒数填充
    result[0][0] = -1;
    result[1][0] = 1;
    for(int k = 2; k < N; k++)
    {
        f = sqrt((double)k * (double)k - 1.0) / (double)k;
        for(int i = 0;i <= k; i++)
        {
            for(int j = 0; j <= k - 1; j++)
            {
                result[i][j] *= f;
            }
        }
        r = -1 / (double)k;
        for(int i = 0; i <= k; i++)
        {
            result[i][k-1] = r;
        }
        for(int j = 0;j <= k-1;j++)
        {
            result[k][j] = 0;
        }
        result[k][k-1] = 1.0;
    }
    for(int row = 0; row < N;row ++,std::cout<<std::endl)
        for(int col = 0;col < N-1;col++)
            printf("%.4lf\t", result[row][col]);
    printf("----------------\n");
    double dataLow = -1.0;
    double dataHigh = 1.0;
    double normalizedHigh = 1.0;
    double normalizedLow = 0.0;
    for(int row = 0; row < N;row ++)
        for(int col = 0;col < N-1;col++)
            result[row][col] = ((result[row][col] - dataLow) / (dataHigh - dataLow))*
            (normalizedHigh - normalizedLow) + normalizedLow;
    for(int row = 0; row < N;row ++,std::cout<<std::endl)
        for(int col = 0;col < N-1;col++)
            printf("%.4lf\t", result[row][col]);
}