算法简介
算法定义
解决特定问题的步骤描述,在计算机中表现为指令的有限序列,每条指令表示一个或多个操作
算法的特性
输入
输出
有穷性
确定性
可行性
算法设计的要求
正确性
能正确反映问题并解决问题
- 算法程序没有语法错误
- 算法程序对正确的输入有正确的结果
- 算法程序对非法的输入能给出满足规格的说明
- 算法程序对于精心选择的故意刁难的数据也能有满足的结果
可读性
代码一目了然,便于阅读沟通和交流健壮性
对不合法的输入也能处理,而不是产生异常时间效率高和存储量低
尽量满足高效且低空间。衡量算法效率的方法
事后统计
对数据进行分析事前分析估算
对算法进行数学估算算法分析
函数的渐进增长
给定两个函数f(n)和g(n),如果存在一个整数N,对于所有的n>N,f(n)总是大于g(n),那么说f(n)增长渐进快于g(n)
| f(n)=3n+1 | g(n)=2n+3 | n | N |
|---|---|---|---|
| 4 | 5 | 1 | 1 |
| 7 | 7 | 2 | 2 |
| 10 | 9 | 3 | 3 |
N是0-1的时候g(n)快,大于2时f(n)快。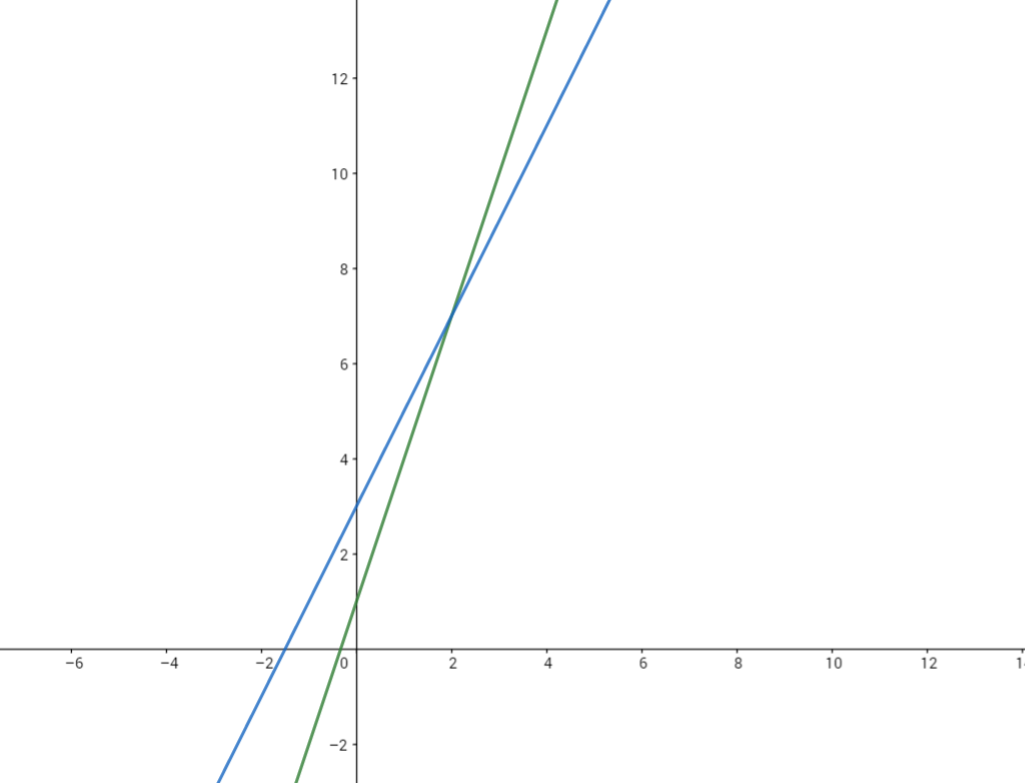
相比之下根据函数性质,多项式中的常数也并不重要,不影响N的取值。
但是相比于n前的系数不同,n的次方增长的更快。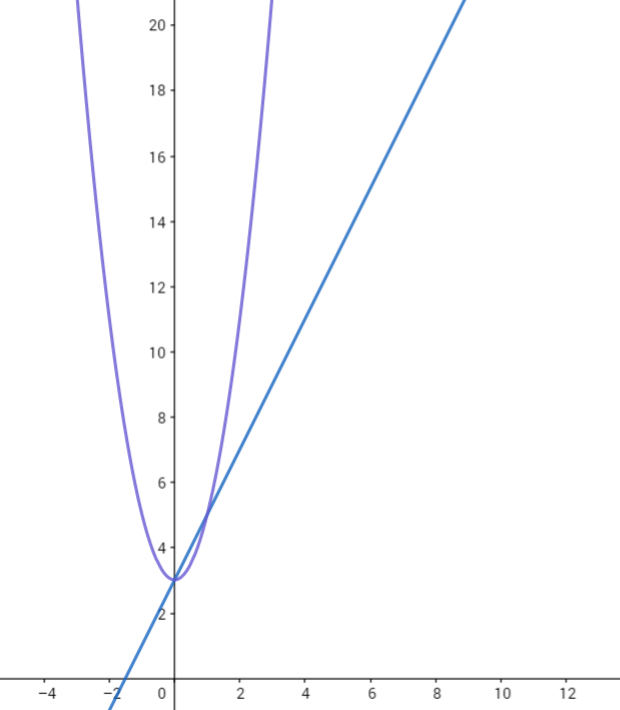
而和不同的阶数相比,差别更大
所以判断一个算法的效率时,更应该关注算法主项的阶数
时间复杂度
定义
在进行算法分析时,语句执行的总次数T(n)是关于问题规模n的函数,进而分析T(n)随n的变化情况而确定T(n)的数量级。
推导大O阶的方法
- 用数字1代表运行时间中的所有假发常数
- 在修改后的运行次数中,只保留最高次项
- 如果最高阶项存在且系数不是1,那么就变成1
一般的算法阶
常数阶
int i = 0,n = 100,sum=0;sum=(1+i)*n/2;printf("%d",sum);//各执行一次,n是3,O(1)
int i = 0,n = 100,sum=0;sum=(1+i)*n/2;sum=(1+i)*n/2;sum=(1+i)*n/2;sum=(1+i)*n/2;sum=(1+i)*n/2;sum=(1+i)*n/2;sum=(1+i)*n/2;sum=(1+i)*n/2;printf("%d",sum);//不论执行多少次,都是O(1)
线性阶
一个执行n次的for循环就是一个线性阶O(n) ```cpp
int i, sum = 0, n = 100; / 执行1次 / for(i = 1; i <= n; i++) / 执行了n+1次 / { sum = sum + i; / 执行n次 / } printf(”%d”, sum); / 执行1次 /
<a name="QHbAf"></a>### 平方阶一个执行n次的for循环中嵌套了一个执行n次的for循环,那么执行次数就是nxn<br />是一个平方阶O(n^2)```cppint i, j, x = 0, sum = 0, n = 100; /* 执行一次 */for(i = 1; i <= n; i++){for (j = 1; j <= n; j++){x++; /* 执行n×n次 */sum = sum + x;}}printf("%d", sum); /* 执行一次 */
对数阶
int count = 1;while count < n){count = count * 2;/* 时间复杂度为O(1)的程序步骤序列 */}
常见的时间复杂度
由快到慢
| 执行次数 | 阶 | 简写 |
|---|---|---|
| 12 | O(1) | 常数阶 |
| 5log_2 n+20 | O(logn) | 对数阶 |
| 2n+3 | O(n) | 线性阶 |
| 2n+3nlog_2 n+30 | O(nlogn) | nlogn阶 |
| 2n^2+2 | O(n^2) | 平方阶 |
| n^3+n^2+2 | O(n^3) | 立方阶 |
| 2^n | O(2^n) | 指数阶 |
| n(n-1)(n-2)…1 | O(n!) | 阶乘阶 |
| n^n | O(n^n) | 无穷阶 |
最坏情况与平均情况
算法分析中的阶都是在最坏情况下得出的,平均运行时间是所有情况中最有意义的,因为他是期望的运行时间。
一般没有特殊说明的情况下,都是指最坏时间复杂度

