基础概念
逻辑状态
表示0和1两种唯一确定状态的事物,一般0表示假的或是无效的
1表示有效的,真的。
逻辑变量
一种变量关系只有1和0两种逻辑状态,在电路中用H表示高电压,用来表示1这种真的逻辑状态
0表示假或是失效用低电压
逻辑电平
高电压表示H,即为真或1
反之是L,表示假或0
高低是相对概念,在不确定区间是错误的
高低是人为规定的,可以表示相反的概念
逻辑正负约定
分为正逻辑规定和佛罗基规定
例如 1 表示 H 高电平是正逻辑
反之是负逻辑
| H(高电压) | 1(真) | 正逻辑规定 |
|---|---|---|
| L(低电压) | 0(假) | 负逻辑规定 |
逻辑代数
逻辑函数
逻辑函数的表示方法
真值表法
逻辑表达式
卡诺图
逻辑代数的基本运算
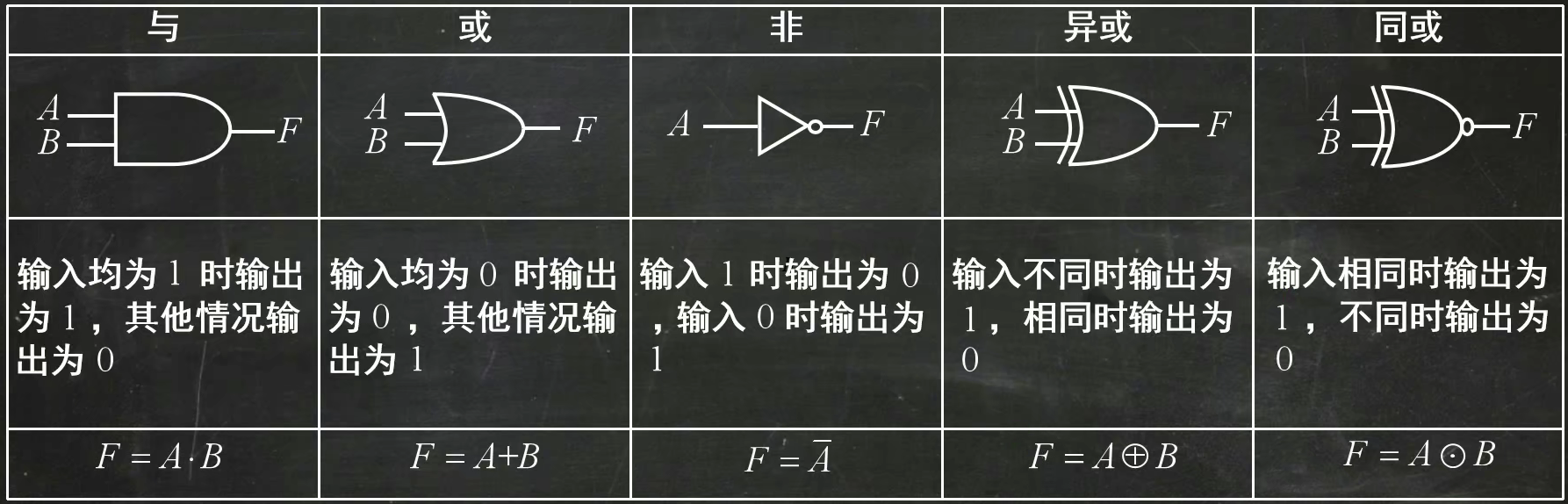
与运算
逻辑乘法 结果叫做逻辑积
F = AxB 或是 F = A · B;
其逻辑电路为与门(AND GATE)
或运算
逻辑加 结果叫做逻辑和
F = A + B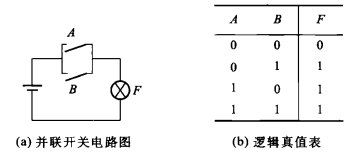
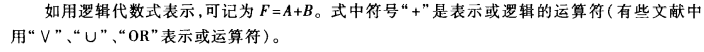
或门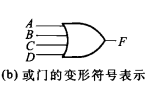 (OR GATE)
(OR GATE)
非运算
复合运算
异或
同或
与非门和或非门

逻辑代数的基本定理
逻辑代数基本公理
逻辑代数的基本公理是基本假定,他说客观存在的现象,可以用真值表验证,但是无需证明
A + 0 = A
A + 1 = 1
A 1 = A
A 0 = 0
0-1l律是基本的代数规律
与或非运算是没有顺序的,因此交换律和分配律都成立
互补律体现了非的互补性,重叠律体现了与或运算的恒真性质
逻辑代数的定理
吸收定理
德摩根律(反演定律)
德摩根律可以将与和或进行互补运算,可以大大简化逻辑变换的过程
多余项定理
三态门
高电平
低电平
高阻态
断开连接状态
集电极开路门
逻辑代数规则
代入规则
反演规则(香农定理)
任何函数求反函数的过程是反演过程。
把所有的变量取反,0变成1,与变成或,即可得到反演结果。
使用反演规则是必须保证运算顺序不变1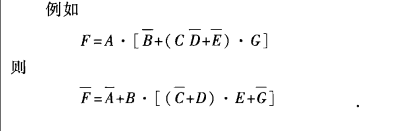

解题步骤:
(1)与项加括号
(2)反演,长非号不动
(3)与运算变成或运算
(4)或运算变成与运算
对偶规则
把逻辑函数中的0变成1,与变成或,但是不取非,保持变量不变,就得到了对偶函数
解题步骤
(1)与项加括号
(2)对偶,长非号不动
(3)与运算变成或运算
(4)或运算变成与运算
输入变量不做变化
逻辑函数性质
复合逻辑的性质
与非逻辑(NotAND)(NAND)
是正常的与门连接非门组成的。
与非-与非表达式
解题步骤
(1)化为与或式
(2)加入两个长非号
(3)利用反演规则化简
最小项
两个变量A,B可以构成四个最小项
最小项是包含所有输入的与项
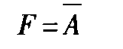
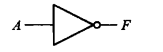 (NOT GATE)
(NOT GATE)