卷积神经网络简介

1.背景和简介

和全连接神经网络一样，卷积神经网络中的每一个节点都是一个神经元。在全连接神经网络中，每相邻两层之间的节点都有边相连，于是一般会将每一层全连接层中的节点组织成一列，方便展示结构。而对于卷积神经网络，相邻两层之间只有部分的节点相连，为了展示每一层神经元的维度，一般会将每一层卷积层的节点组织成一个三位矩阵。所以，卷积神经网络和全连接结构唯一的区别就是神经网络中相邻两层的连接方式。
全连接神经网络处理图像的最大问题就是全连接层的参数太多。假设MNIST 28x28x1的图片，第一层隐藏层的节点数为500，那么参数的个数就是28x28x500 + 500 个。当图片更大时候，参数更多。参数过多容易导致计算量剧增和过拟合的问题。
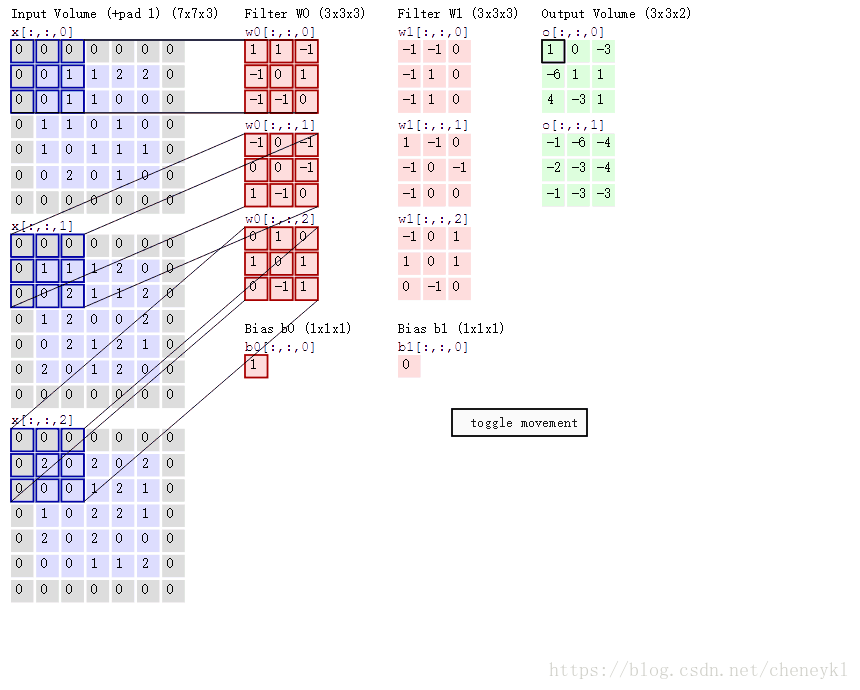
下图是输入层到卷积层的过程。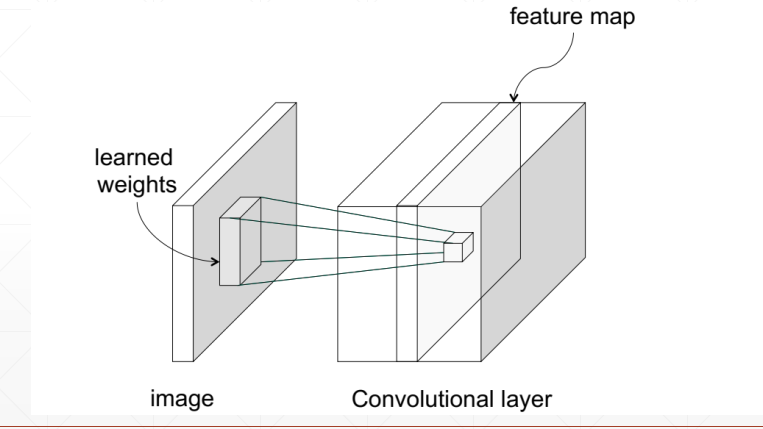

比较经典的LeNet-5模型，是Yann LeChun教授在1998年提出的，它的结构是：

卷积层 =》 池化层 =》 卷积层 =》 池化层 =》 全连接层 =》 全连接层 =》 全连接层

2. Feature Map的理解

在cnn的每个卷积层，数据都是以三维形式存在的。你可以把它看成许多个二维图片叠在一起（像豆腐皮竖直的贴成豆腐块一样），其中每一个称为一个feature map。整个堆叠的长度就是深度。
在输入层，如果是灰度图片，那就只有一个feature map；如果是彩色图片（RGB），一般就是3个feature map（红绿蓝）
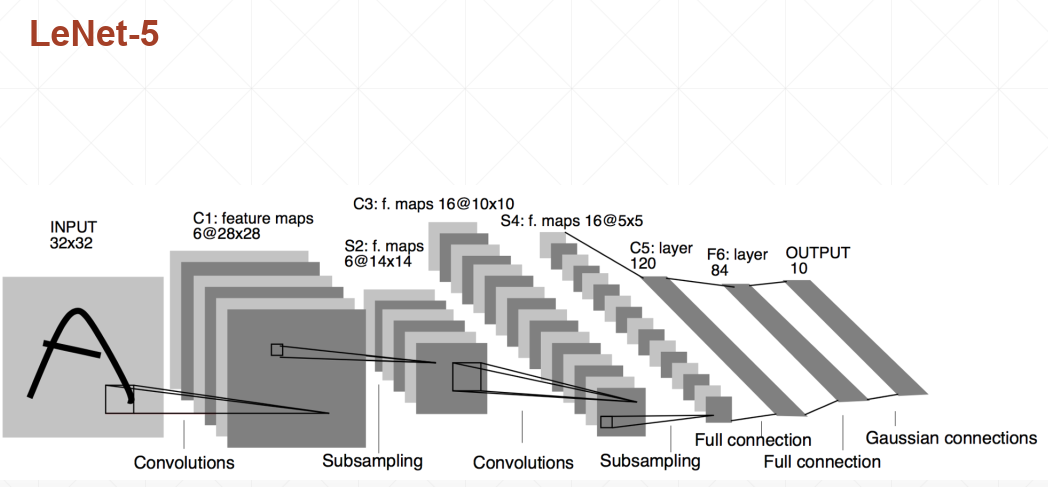
下图中三大部分依次是：
输入RGB图片、卷积核（也称过滤器）、卷积结果（输出）。 代表卷积操作，最左部分三片代表3个feature map;
ps：如果是灰色图片（二维），则最左只有一片代表一个feature map，对应的卷积核（也是二维）

————————————————————————

————————————————————————

其它层：层与层之间会有若干个卷积核（kernel）（也称为过滤器），
*(卷积核深度与初始图片的通道数一致）
上一层所有feature map 对应的跟某个卷积核的所有层做卷积，结果相加（或者再加上偏置），都会产生下一层的一个feature map，有N个卷积核，下层就会产生N个feather map。
即：输入图片不论通道数是1（灰色）还是3（彩色）or其他值，经过卷积核处理后，都会统一拍平成深度为1的feature map。
有几个卷积核就生成几个feature map，与输入图片的通道数无关。

3 卷积运算

影响卷积运算的因素有：步幅(stride)为S，填充(padding)为P，数据数据的高和宽(H,W),滤波器的大小为（FH, FW），输出大小是（OH, OW）。

一般地，上式代入以后都要除尽，说明feature map可以完整映射处理输入数据。