一、概念
二、求解过程
三、常用损失函数和梯度
- 3.1 均方和（Mean Squared Error）
- 3.2 交叉熵Cross Entropy Loss
四、Softmax函数（暂时放这边）
参考文献

一、概念

在机器学习中，我们通常需要对问题进行建模，然后可以得到一个成本函数(cost function)，通过对这个成本函数进行最小化，我们可以得到我们所需要的参数，从而得到具体的模型。这些优化问题中，只有少部分可以得到解析解(如最小二乘法)，而大部分这类优化问题只能迭代求解，而迭代求解中两种最常用的方法即梯度下降法与牛顿法。
梯度概念是建立在偏导数与方向导数概念基础上的。

偏导数只能表示多元函数沿某个坐标轴方向的导数，多元函数在非坐标轴方向上也可以求导数，这种导数称为方向导数。很容易发现，多元函数在特定点的方向导数有无穷多个，表示函数值在各个方向上的增长速度。一个很自然的问题是：在这些方向导数中，是否存在一个最大的方向导数，如果有，其值是否唯一？为了回答这个问题，便需要引入梯度的概念。
一般来说，梯度可以定义为一个函数的全部偏导数构成的向量(这一点与偏导数与方向导数不同，两者都为标量)。即：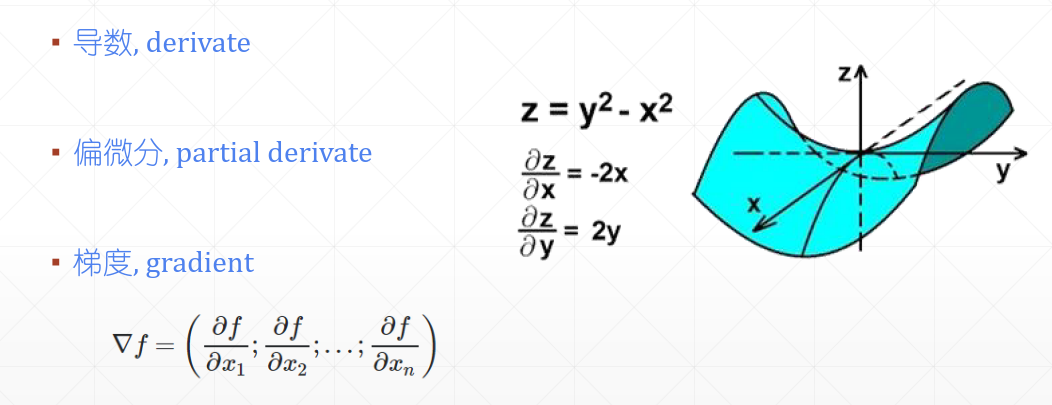

二、求解过程

那怎么样求解一个函数的的梯度呢？
假设我们有一个二元二次方程，如下图，左边是求解的计算迭代公式，右边是步骤。

三、常用损失函数和梯度

常用损失函数有均方和和交叉熵，实际使用一般使用交叉熵。实测经验是，交叉熵可以在训练次数较少的情况下就到达一个比较高的测试准确率水平。

3.1 均方和（Mean Squared Error）

均方和是比较常用的损失函数，公式如下：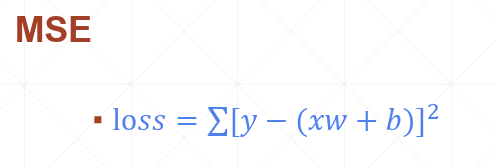

梯度计算：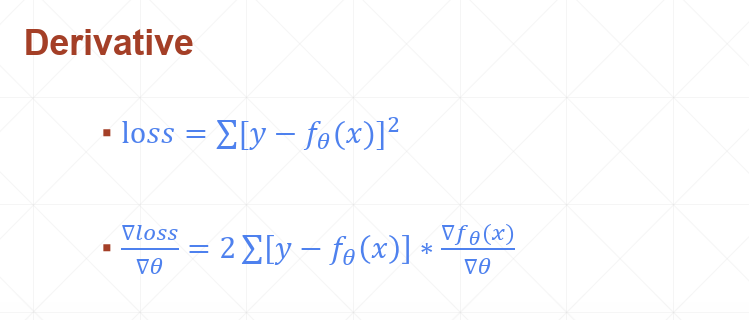

PyTorch有两种API来完成梯度计算，使用

示例1, 用torch.autograd.grad api来完成梯度计算：
1）15行 mse = F.mseloss(x * w, torch.ones(1)) 代码就是根据公式求解；
2）18行 result = torch.autograd.grad(mse, [w] 代码是计算的；
3）一般地，有了这个梯度result，我们就可以根据：![](https://cdn.nlark.com/yuque/__latex/29a92912e3a4689b56f8d1a8a67ce770.svg#card=math&code=w%7Bn%2B1%7D%20%3D%20w_n%20-%20n%2A%5Cfrac%7Bdloss%7D%7Bdw%7D&height=40&width=169) ，然后不断迭代寻找极小值。

import torch
from torch.nn import functional as F
# x为dim为1，长度为1的张量
x = torch.ones(1)
# w为dim为1， 长度为1， 值为2的张量
w = torch.full([1], 2)
# 告诉pytorch w变量是需要更新导数的
w.requires_grad_()
print(w)
# 打印结果None
print(w.grad)
# 第一个参数是pred, 第二个参数是label
mse = F.mse_loss(x * w, torch.ones(1))
#grad第一个参数是一个维度为1，长度为1的值
result = torch.autograd.grad(mse, [w])
# (tensor([2.]),)
print(result)
# 打印结果None
print(w.grad)

注意：上面12行和22行，说明使用autograd.grad的方法不会将梯度结果更新到tensor中，即通过tensor.grad方法只能获取到None。

示例2：用backward()来完成梯度计算：

import torch
from torch.nn import functional as F
# x为dimension为1，长度为1的张量
x = torch.ones(1)
# w为dim为1， 长度为1， 值为2的张量
w = torch.full([1], 2)
# 告诉pytorch w变量是需要更新导数的
w.requires_grad_()
print(w)
# 打印结果 None
print(w.grad)
# 第一个参数是pred, 第二个参数是label
mse = F.mse_loss(x * w, torch.ones(1))
# backward方法不返回任何值,但是会更新梯度到所有的变量上
mse.backward()
# 打印结果 tensor([2.])
print(w.grad)

注意：上面10行和18行，说明使用backward的方法将梯度结果更新到tensor中，即通过tensor.grad的方法可以获取到求导的值。

3.2 交叉熵Cross Entropy Loss

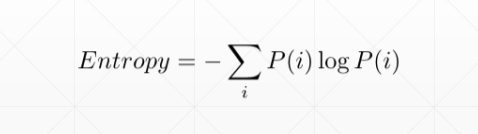
示例：

import torch
from torch.nn import functional as F
x = torch.randn(1, 784)
w = torch.randn(10, 784)
logits = x @ w.t()
print(logits.shape)
print(logits)
pred = F.softmax(logits, dim=1)
pred_log = torch.log(pred)
# 注意这里传入的是: logits, cross_entropy内部会去做softmax和log
# 注意: CE = logits + softmax + log
result = F.cross_entropy(logits, torch.tensor([3]))
# 打印tensor(19.9642)
print(result)
result = F.nll_loss(pred_log, torch.tensor([3]))
# 打印tensor(19.9642)
print(result)

四、Softmax函数（暂时放这边）

在分类的问题中，经常要将分类结果以概率的形式展示出来。我们知道，概率有两个性质：1）预测的概率为非负数；2）各种预测结果概率之和等于1。softmax就是将在负无穷到正无穷上的预测结果按照这两步转换为概率的。

参考文献

https://blog.csdn.net/weixin_42018112/article/details/88079998
龙永图老师pytorch系列教程

AI

梯度下降（gradient decent）